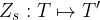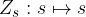Le isometrie sono casi particolari delle trasformazioni lineari nel piano che possiamo definire in questo modo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La trasformazione identica che abbiamo descritto nell'esempio, ci sarà utile in alcune definizioni che daremo tra poco.
Concetti introduttivi
Tutte le isometrie nel piano si possono ricondurre a tre tipologie fondamentali:
Un esempio di applicazione di ciascuna delle tre tipologie è illustrato nelle figure seguenti:
Prima di procedere con lo studio di queste tre categorie di trasformazioni, definiamo meglio che cosa intendiamo in generale con il termine simmetria quando parliamo di una forma geometrica:
Si dice che una forma geometrica ha una simmetria se esiste un'isometria (diversa dalla trasformazione identica) che trasforma la figura in se stessa.
Possiamo quindi dire che una simmetria è una particolare isometria tale che
l' insieme immagine coincide con l' insieme origine
almeno un punto immagine non coincide con il punto origine
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Traslazioni
Possiamo definire una traslazione come uno spostamento rigido di tutti i punti della figura in una stessa direzione per una determinata lunghezza.
In matematica, uno spostamento caratterizzato da una lunghezza e da una direzione (oltre che un verso) è descritto da un vettore. Utilizzando i vettori possiamo quindi definire la traslazione in questo modo:
Una traslazione è una trasformazione del piano caratterizzata da un vettore 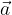 tale che ad ogni punto T dell'insieme origine corrisponde il punto immagine T' ottenuto applicando
tale che ad ogni punto T dell'insieme origine corrisponde il punto immagine T' ottenuto applicando 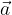 a T. In formule:
a T. In formule:
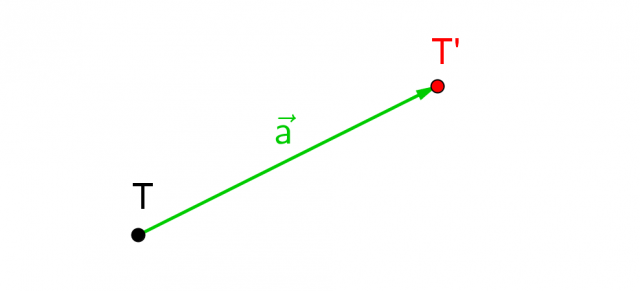
Graficamente, possiamo illustrare una traslazione in questo modo:
Ricordando anche l'esempio riportato all'inizio del capitolo, possiamo elencare le proprietà di una traslazione in questo modo:
A ogni punto al quale viene applicato il vettore 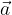 nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
Conserva l'inclinazione di ogni linea rispetto a un riferimento fisso
Mantiene invariate le distanze tra i punti (è una trasformazione isometrica)
Per ulteriori esempi e approfondimenti vedere il capitolo Traslazioni.
Rotazioni
Una rotazione è una funzione che a ciascun punto T dell'insieme origine associa il punto T' ottenuto ruotando T di un angolo 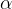 assegnato rispetto a un punto fisso S. In formule:
assegnato rispetto a un punto fisso S. In formule:
Il punto S intorno al quale avviene la rotazione si chiama centro di rotazione. L'angolo 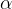 è detto angolo di rotazione.
è detto angolo di rotazione.
Il centro di rotazione S è l'unico punto fisso della trasformazione. Nelle tre dimensioni, esso può essere pensato come il punto d'intersezione del piano della trasformazione con un asse di rotazione perpendicolare a tale piano e passante per S.
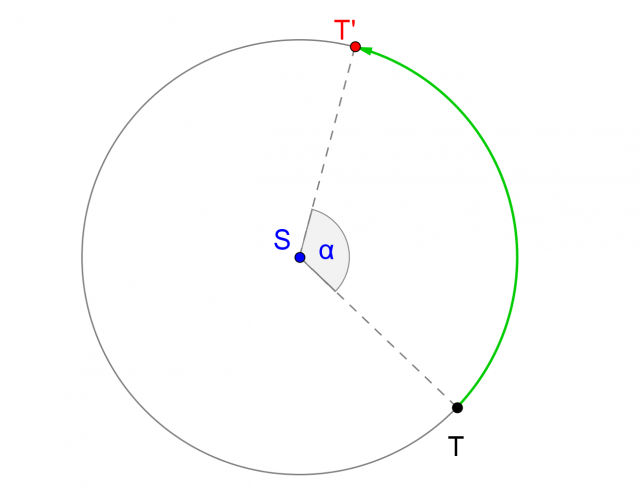
Per ogni punto T della figura origine, possiamo immaginare la rotazione di centro S come uno spostamento secondo un arco di ampiezza 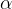 lungo la circonferenza che contiene T e ha per centro S. Anche il punto T' appartiene quindi alla stessa circonferenza.
lungo la circonferenza che contiene T e ha per centro S. Anche il punto T' appartiene quindi alla stessa circonferenza.
Ricordando anche l'immagine illustrata come esempio all'inizio del capitolo, possiamo riassumere le proprietà della rotazione in questo modo:
La distanza di T da S è uguale alla distanza di T' da S. In formule:
I punti T e T' sono estremi di un arco appartenente alla circonferenza di centro S e raggio r, tale che:
L'angolo di rotazione 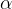 coincide con l'ampiezza del settore circolare di centro S ed estremi T e T '. In formule:
coincide con l'ampiezza del settore circolare di centro S ed estremi T e T '. In formule:
Con l'aiuto della figura possiamo individuare le seguenti proprietà delle rotazioni, che sono naturalmente anche dimostrabil a partire dalle proprietà geometriche della trasformazione:
A ogni punto al quale viene applicata la rotazione nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
L'immagine di un segmento non è parallela al segmento di partenza
Mantiene invariate le distanze tra i punti (è una trasformazione isometrica)
Gruppi di rotazioni e simmetria centrale
Tra le rotazioni, hanno un'importanza particolare quelle in cui l'insieme origine e l'insieme immagine coincidono.
L'insieme a cui è applicata la rotazione si dice allora avere un centro di simmetria. Lo studio delle rotazioni intorno al centro di simmetria è molto interessante perchè permette di raggruppare tra di loro secondo delle precise proprietà tutte le rotazioni che "funzionano" su una determinata figura, ovvero tutte le rotazioni che sono capaci di trasformare la figura in se stessa. Si parla in questo caso di un gruppo di rotazioni.
Un caso particolare è poi rappresentato dalla rotazione di 180°, che ha delle caratteristiche speciali rispetto alle altre rotazioni: soltanto alla rotazione di 180° intorno al centro di simmetria è riservato il nome di simmetria centrale.
Per ulteriori esempi e approfondimenti vedere il capitolo Rotazioni.
Gruppi di rotazioni
Alcune figure geometriche regolari possono avere un centro di simmetria S rispetto al quale alcune rotazioni trasformano la figura in se stessa.
In geometria piana è interessante studiare i casi in cui l'angolo di rotazione 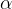 che trasforma una figura in se stessa è una frazione propria dell'angolo giro.
che trasforma una figura in se stessa è una frazione propria dell'angolo giro.
In formule, esistono un intero n e un intero k < n tali che:
Applicando n volte questa rotazione di centro S e angolo 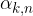 , otteniamo la trasformazione identica: ogni punto viene trasformato in se stesso.
, otteniamo la trasformazione identica: ogni punto viene trasformato in se stesso.
Inoltre, ogni rotazione di angolo 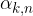 può essere ottenuta applicando k volte di seguito la rotazione di angolo
può essere ottenuta applicando k volte di seguito la rotazione di angolo 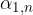 .
.
Per questo si dice che tutte le rotazioni di centro S e angolo 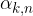 formano un gruppo, che indichiamo con
formano un gruppo, che indichiamo con 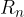 .
.
Una figura che viene trasformata in se stessa da una rotazione di angolo 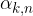 , è trasformata in se stessa da tutte rotazioni del gruppo
, è trasformata in se stessa da tutte rotazioni del gruppo 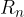 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In generale, ogni poligono regolare di n lati è simmetrico rispetto al gruppo di rotazioni 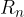 applicato al suo centro e la rotazione minima che lo trasforma in se stesso ha ampiezza
applicato al suo centro e la rotazione minima che lo trasforma in se stesso ha ampiezza
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Simmetria centrale
Tra tutte le rotazioni nel piano, la rotazione di 180° ha delle caratteristiche particolari.
Prendiamo ad esempio un triangolo e ruotiamolo di 180° rispetto ad un punto S esterno ad esso:
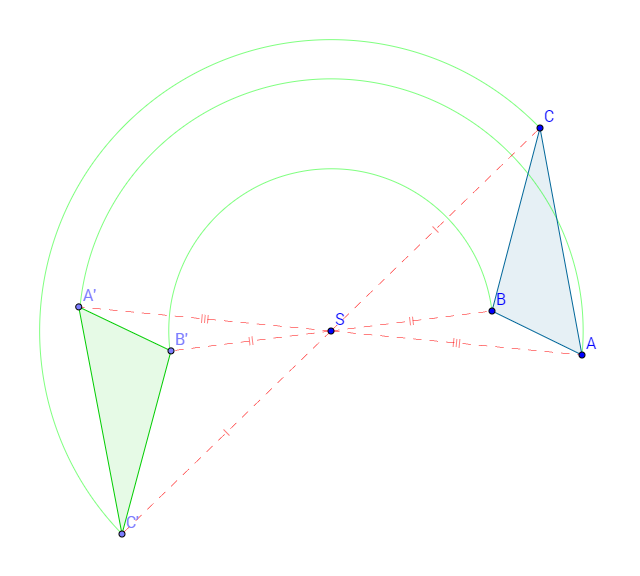
Il triangolo ABC e la sua immagine A'B'C' ruotata di 180° intorno al punto S
Se osserviamo la figura, possiamo notare (e dimostrare geometricamente!) che il centro di simmetria S è sempre il punto medio del segmento che unisce ogni punto con la sua immagine ruotata.
In altre parole, possiamo ottenere la stessa immagine finale A'B'C' se invece di ruotare la figura di 180°, costruiamo il segmento che congiunge ogni punto con il centro S e lo prolunghiamo di un segmento della stessa lunghezza dal lato opposto di S:
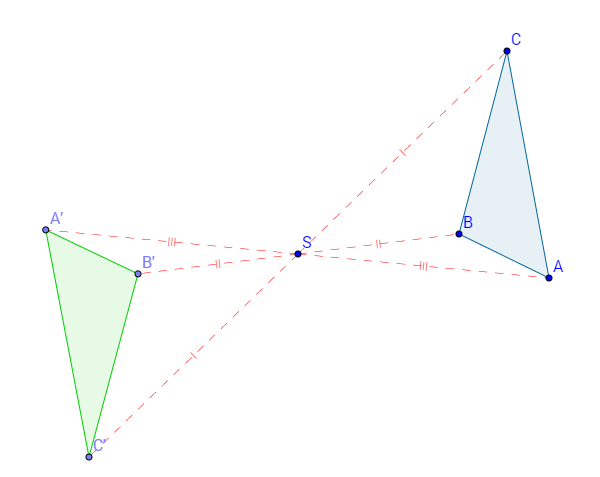
Il triangolo ABC e la sua immagine A'B'C' presentano una simmetria centrale rispetto a S
La simmetria centrale ha le seguenti interessanti proprietà:
l'immagine di un segmento è parallela al segmento di partenza (anche se gli estremi sono scambiati)
si mantiene l'orientazione della figura (anche se la posizione nel piano è capovolta)
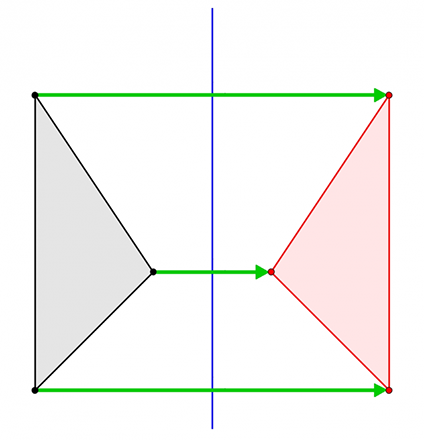
Simmetrie assiali
Tutte le isometrie che abbiamo visto finora, mantengono l' orientazione della figura.
Se ad esempio abbiamo assegnato ai vertici della figura delle lettere ordinandole in senso antiorario, anche i punti corrispondenti nell'immagine saranno ordinati in senso antiorario.
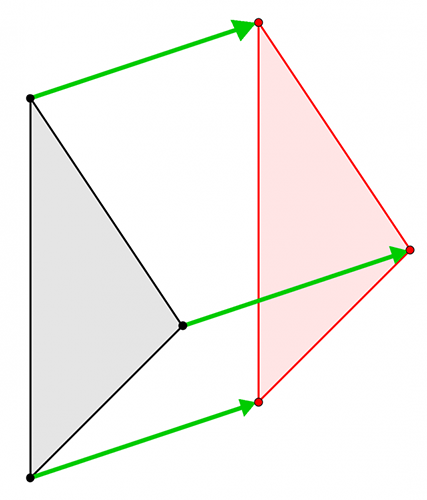
Ci sono invece altri tipi di isometrie che "ribaltano" la figura: se assegniamo dei nomi ai vertici procedendo in senso antiorario, i punti corrispondenti nell'immagine saranno ordinati in senso orario e viceversa.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se osserviamo la figura ottenuta nell'esempio precedente, possiamo definire una simmetria assiale in questo modo:
Ricordando le proprietà dell'asse di un segmento, possiamo formalizzare la definizione di simmetria assiale in questo modo:
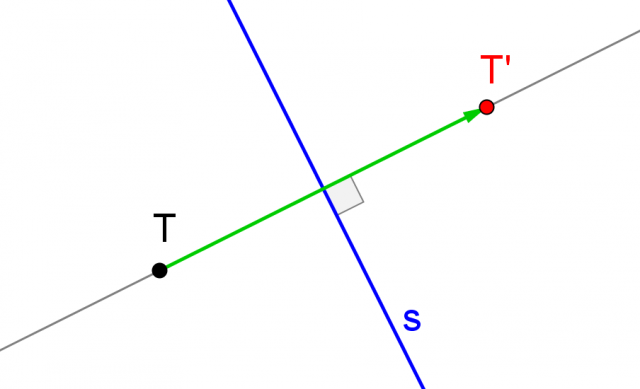
Data una retta  del piano, l'isometria
del piano, l'isometria
è una simmetria assiale se e solo se ha le seguenti proprietà:
il segmento TT' è perpendicolare ad 
La distanza di  dal punto T' è pari alla distanza di
dal punto T' è pari alla distanza di  dal punto T
dal punto T
La retta  si chiama asse di simmetria della trasformazione.
si chiama asse di simmetria della trasformazione.
Poichè un punto origine e la sua immagine mantengono la stessa distanza dall'asse  e appartengono alla retta perpendicolare all'asse, i punti della retta
e appartengono alla retta perpendicolare all'asse, i punti della retta  rimangono fissi rispetto alla simmetria assiale:
rimangono fissi rispetto alla simmetria assiale:
Ricordando anche l'esempio riportato all'inizio del capitolo, possiamo elencare le proprietà di una simmetria assiale in questo modo:
A ogni punto al quale viene applicato il vettore 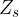 nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
L'inclinazione si conserva soltanto per le rette perpendicolari o parallele all'asse di simmetria
Mantiene invariate le distanze tra i punti (è una trasformazione isometrica)




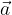 tale che ad ogni punto T dell'insieme origine corrisponde il punto immagine T' ottenuto applicando
tale che ad ogni punto T dell'insieme origine corrisponde il punto immagine T' ottenuto applicando 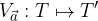
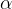 assegnato rispetto a un punto fisso S. In formule:
assegnato rispetto a un punto fisso S. In formule: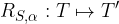
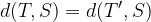
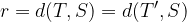
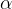 coincide con l'ampiezza del
coincide con l'ampiezza del 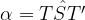
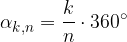
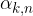 , otteniamo la trasformazione identica: ogni punto viene trasformato in se stesso.
, otteniamo la trasformazione identica: ogni punto viene trasformato in se stesso.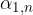 .
.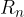 .
.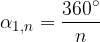


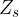 rispetto alla retta
rispetto alla retta  è un'isometria che trasforma ogni punto T dell'insieme origine in una immagine T' appartenente al piano di T ed
è un'isometria che trasforma ogni punto T dell'insieme origine in una immagine T' appartenente al piano di T ed