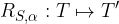Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti


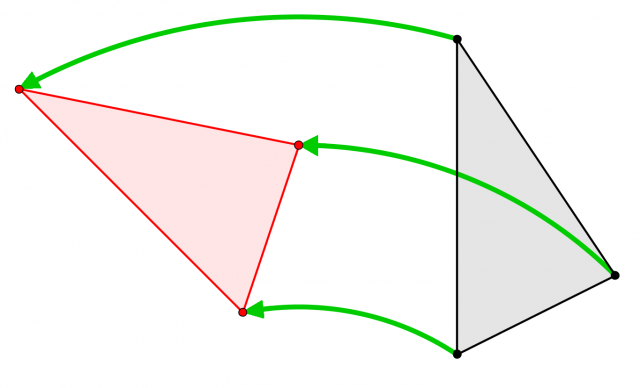
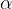 assegnato rispetto a un punto fisso S. In formule:
assegnato rispetto a un punto fisso S. In formule: