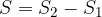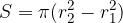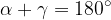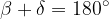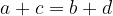Il cerchio è una figura geometrica piana definita da:
centro (che indichiamo con S);
Il centro determina la posizione del cerchio nel piano mentre il raggio ne determina la grandezza.
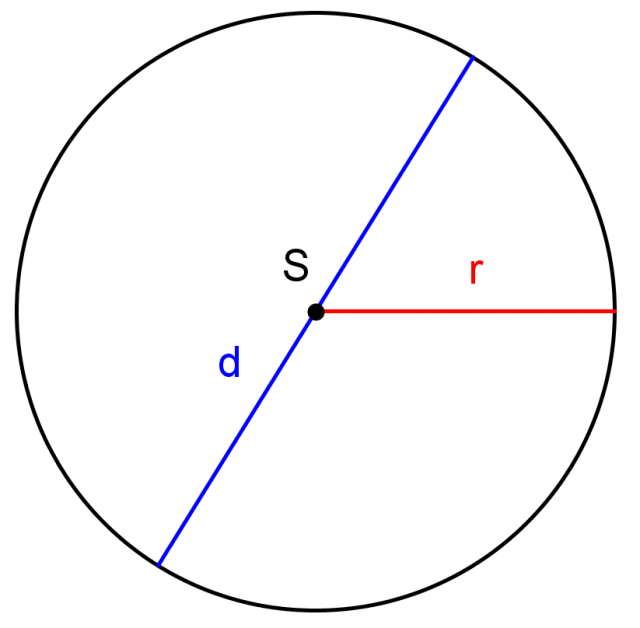
Possiamo definire anche il diametro, la distanza d, che è il doppio del raggio.
Definizione
Per prima cosa mettiamo in chiaro la differenza tra circonferenza e cerchio.
La circonferenza
La circonferenza è una curva chiusa formata dall'insieme dei punti del piano che hanno distanza dal centro S pari al raggio r:
La circonferenza è quindi curva che comprende tutti i punti che hanno la stessa distanza dal centro: con il compasso disegniamo una circonferenza, con raggio pari all'apertura del compasso.
Se aggiungiamo a questo insieme tutti i punti interni alla curva chiusa, otteniamo il cerchio, trattato nel paragrafo seguente.
Il cerchio
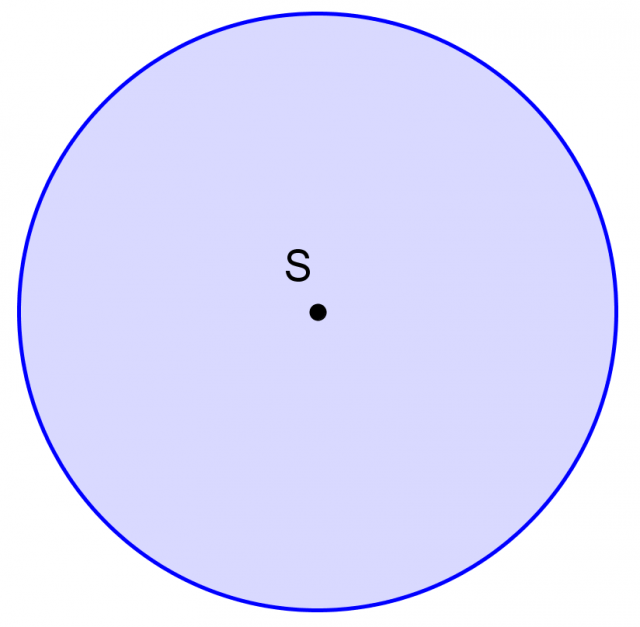
Il cerchio è una figura piana formata dall'insieme dei punti del piano che hanno distanza dal centro S minore o uguale al raggio r:
Non bisogna mai dimenticare che la circonferenza fa parte del cerchio!
Riassunto dei concetti
Cerchiamo di riassumere i concetti illustrati finora.
Il cerchio è l'insieme di tutti i punti del piano che hanno distanza dal centro S minore o uguale al raggio r. E' una figura piana e convessa.
La circonferenza è l'insieme di tutti i punti del piano che hanno distanza dal centro S esattamente uguale al raggio r. E' una curva chiusa.
Il centro è un punto interno al cerchio. Esso appartiene al cerchio ma non alla circonferenza. E' il punto del piano equidistante da tutti i punti della circonferenza. Lo indichiamo con la lettera maiuscola S.
Il raggio è la distanza tra qualunque punto della circonferenza e il centro S. Lo indichiamo con la lettera minuscola r.
Il diametro è la massima distanza tra due punti della circonferenza e la sua misura è pari al doppio del raggio. Lo indichiamo con la lettera minuscola d.
Misura della circonferenza e area del cerchio
Vediamo in questo capitolo come calcolare la lunghezza della circonferenza o l'area del cerchio.
Misura della circonferenza
La circonferenza non è un poligono ma una figura curvilinea. Non parliamo quindi di perimetro visto che il calcolo della sua misura non si può ottenere direttamente. Esso coinvolge infatti il fattore 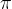 (da leggere: pi-greco), che è un numero irrazionale di solito approssimato con il valore 3,14:
(da leggere: pi-greco), che è un numero irrazionale di solito approssimato con il valore 3,14:
La misura C della circonferenza è pari alla lunghezza del suo diametro moltiplicata per 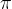 (pi-greco):
(pi-greco):
Ricordiamo il valore di pi-greco:
Area del cerchio
Anche l'area del cerchio coinvolge il fattore 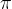 :
:
L'area del cerchio è pari al quadrato del raggio moltiplicato per 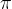 (pi-greco):
(pi-greco):
Ricordiamo il valore di pi-greco:
Per curiosità, riportiamo pi-greco con i primi 100 decimali:
Angoli relativi a un cerchio
Il cerchio non è un poligono, quindi il suo bordo, ovvero la circonferenza, non ha angoli.
Possiamo tuttavia studiare quegli angoli che hanno il vertice sulla circonferenza o nel suo centro e i lati interni o tangenti alla circonferenza stessa. Possiamo studiare anche gli angoli che hanno il vertice esterno al cerchio e i lati tangenti alla circonferenza. Questi due tipi di angoli hanno caratteristiche particolari.
Angoli al centro e angoli alla circonferenza
Sia 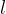 l'arco di circonferenza compreso tra i punti A e B, k l'arco complementare ad
l'arco di circonferenza compreso tra i punti A e B, k l'arco complementare ad 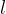 .
.
L'angolo al centro 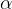 è un angolo che insiste sull'arco
è un angolo che insiste sull'arco 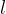 di estremi A e B, con vertice nel centro S della circonferenza.
di estremi A e B, con vertice nel centro S della circonferenza.
L'angolo alla circonferenza 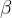 è un angolo che insiste sull'arco
è un angolo che insiste sull'arco 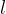 di estremi A e B, con vertice in un punto C appartenente alla circonferenza e situato sull'arco complementare k:
di estremi A e B, con vertice in un punto C appartenente alla circonferenza e situato sull'arco complementare k:
Vediamo un importante teorema che mette in relazione angolo al centro e angolo alla circonferenza.
Teorema dell'angolo al centro.
Un angolo al centro ha ampiezza doppia del corrispondente angolo alla circonferenza:
Teorema (di Talete) dell'angolo alla semicirconferenza
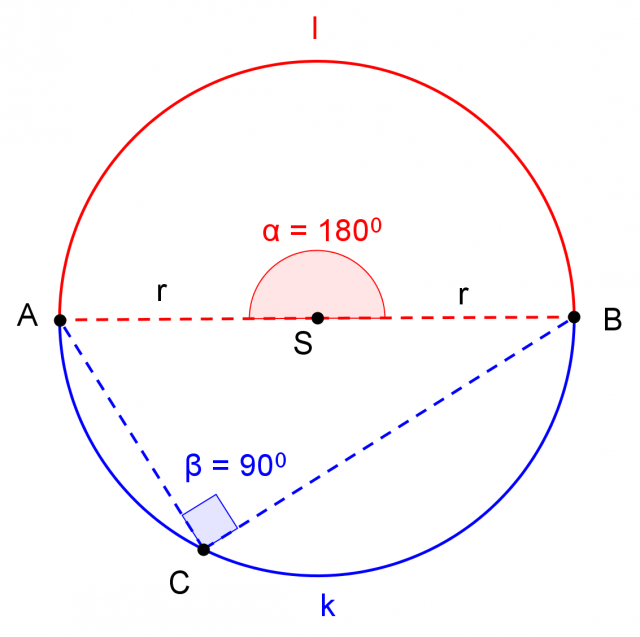
Sia AB un diametro del cerchio. L'arco 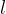 di estremi A e B è allora una semicirconferenza, e così pure l'arco complementare k. L'angolo al centro risulta quindi, in questo caso, l'angolo piatto formato dal diametro AB con vertice nel centro S. Qualunque angolo alla circonferenza che insista su AB, per il teorema dell'angolo al centro, risulta essere un angolo retto.
di estremi A e B è allora una semicirconferenza, e così pure l'arco complementare k. L'angolo al centro risulta quindi, in questo caso, l'angolo piatto formato dal diametro AB con vertice nel centro S. Qualunque angolo alla circonferenza che insista su AB, per il teorema dell'angolo al centro, risulta essere un angolo retto.
Teorema di Talete dell'angolo alla semicirconferenza.
Un qualunque angolo con estremi negli estremi di un diametro e vertice su una semicirconferenza relativa a quel diametro, è un angolo retto. Ovvero: un triangolo inscritto in una semicirconferenza è sempre un triangolo rettangolo.
Parti del cerchio e della circonferenza
Vediamo in quali modi possiamo scomporre la circonferenza e il cerchio. Partiamo con l'arco, una porzione di circonferenza.
Arco di circonferenza
Un arco di circonferenza è una parte della circonferenza delimitata da due dei suoi punti. Due archi di circonferenza con gli stessi estremi e appartenenti alla stessa circonferenza si dicono archi complementari.
Gli archi complementari e i loro estremi esauriscono l'insieme dei punti della circonferenza (nella figura abbiamo indicato con 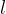 e k i due archi complementari):
e k i due archi complementari):
Un arco di circonferenza i cui estremi siano gli estremi di un diametro, è chiamato semicirconferenza.
Lunghezza di un arco di circonferenza
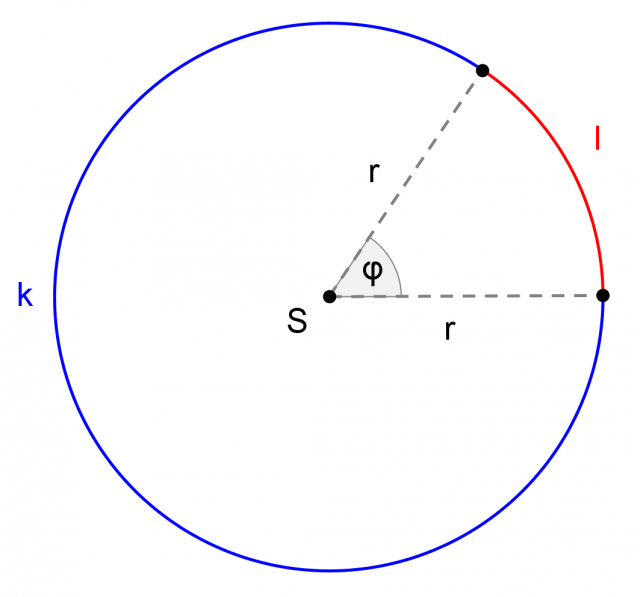
Il rapporto tra la lunghezza dell' arco 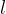 e la lunghezza C dell'intera circonferenza è pari al rapporto tra l'ampiezza del rispettivo angolo al centro e l' angolo giro:
e la lunghezza C dell'intera circonferenza è pari al rapporto tra l'ampiezza del rispettivo angolo al centro e l' angolo giro:
In altre parole, la lunghezza di un arco di circonferenza è direttamente proporzionale all'ampiezza dell'angolo al centro che insiste sopra di esso.
A partire da questa legge di proporzionalità, possiamo scrivere la seguente formula per il calcolo di 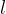 :
:
Corda
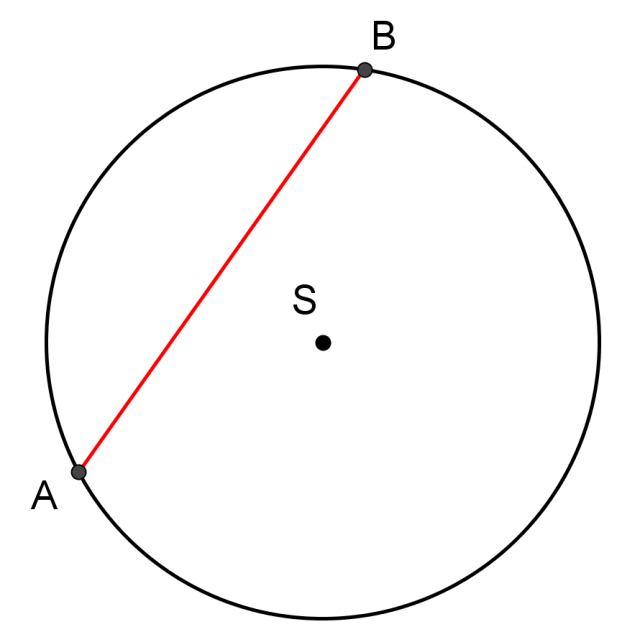
La corda è un segmento che congiunge due punti qualsiasi della circonferenza. Il diametro è la corda di lunghezza massima.
Proprietà della corda
Osserviamo che i segmenti che congiungono gli estremi della corda con il centro della circonferenza sono due raggi, quindi hanno la stessa lunghezza.
Il centro S della circonferenza appartiene sempre all'asse di simmetria della corda AB.
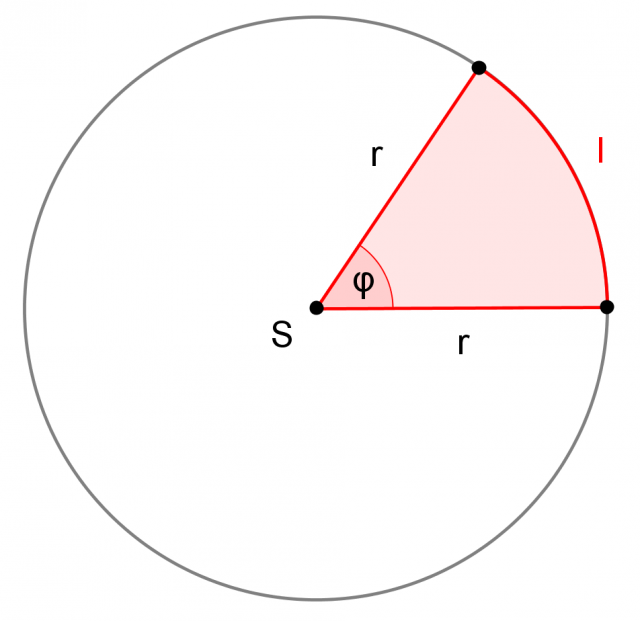
Settore circolare
Un settore circolare è la porzione di cerchio delimitata da due raggi e dall'arco di circonferenza compreso tra i loro estremi:
Area del settore circolare
L'area di un settore circolare sta all'area del cerchio come l'ampiezza dell' angolo al centro individuato dal settore sta all'angolo giro:
Con questa regola di proporzionalità, possiamo scrivere una formula per il calcolo dell'area di un settore circolare:
Area del settore circolare.
Segmento circolare
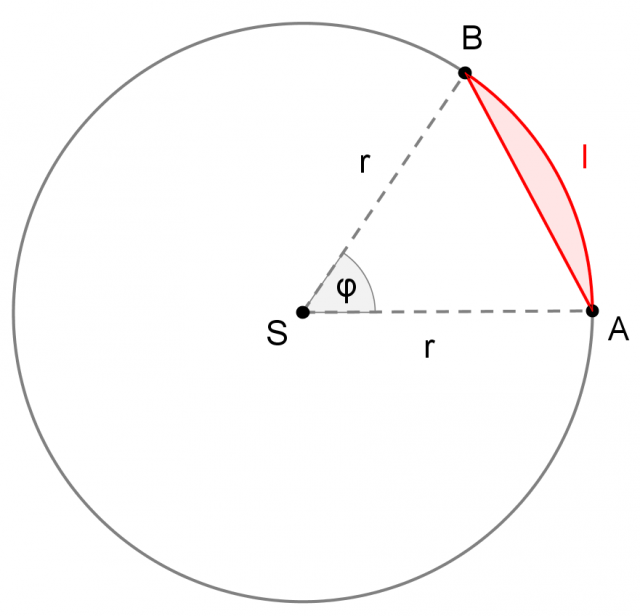
Un segmento circolare è la parte di piano delimitata da un arco di circonferenza e dalla corda che lo sottende:
Area di un segmento circolare
L'area di un segmento circolare si può calcolare a partire dall'area del settore circolare di angolo 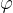 sotteso dalla stessa corda. Si sottrae l'area del triangolo isoscele ABS che ha per lati obliqui i raggi AS e BS del settore circolare e per base la corda AB (vedi immagine qui sopra).
sotteso dalla stessa corda. Si sottrae l'area del triangolo isoscele ABS che ha per lati obliqui i raggi AS e BS del settore circolare e per base la corda AB (vedi immagine qui sopra).
Ricordando la formula per l'area del settore circolare e per quella del triangolo isoscele, possiamo scrivere:
Formula per il calcolo dell'area di segmento circolare.
L'uso di questa formula presuppone che consideriamo soltanto angoli convessi:
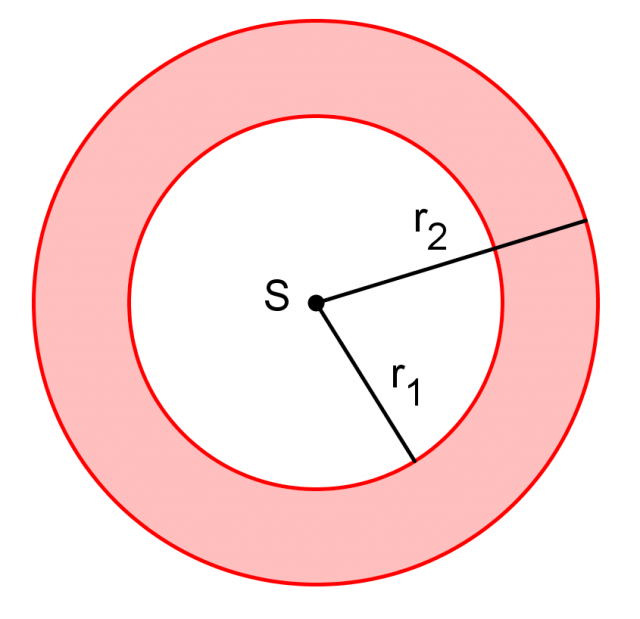
Corona circolare
Una corona circolare è la parte del piano delimitata da due circonferenze concentriche, ovvero con lo stesso centro e raggi diversi.
Indichiamo i due diversi raggi con 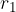 ed
ed 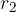 :
:
Area della corona circolare
L'area di una corona circolare si ottiene sottraendo l'area del cerchio minore da quella del cerchio maggiore:
Formula per il calcolo dell'area di una corona circolare.
Posizioni reciproche di una retta e una circonferenza
Una retta appartenente allo stesso piano di una circonferenza può essere:
Secante, se la retta interseca la circonferenza in due punti distinti. La distanza del centro S da una retta secante è minore del raggio r;
Tangente, se la retta incontra la circonferenza in un solo punto chiamato punto di tangenza. La retta tangente è perpendicolare al raggio nel punto di tangenza. La distanza del centro S da una retta tangente è esattamente uguale al raggio r;
Esterna, se la retta non ha punti d'intersezione con la circonferenza. La distanza del centro S da una retta esterna è maggiore del raggio r;
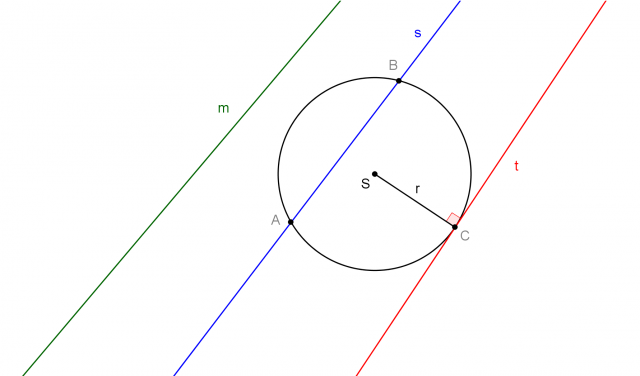
Una retta secante s, una retta tangente t e una retta esterna m
Relazioni tra cerchio e poligoni
Triangolo inscritto in un cerchio
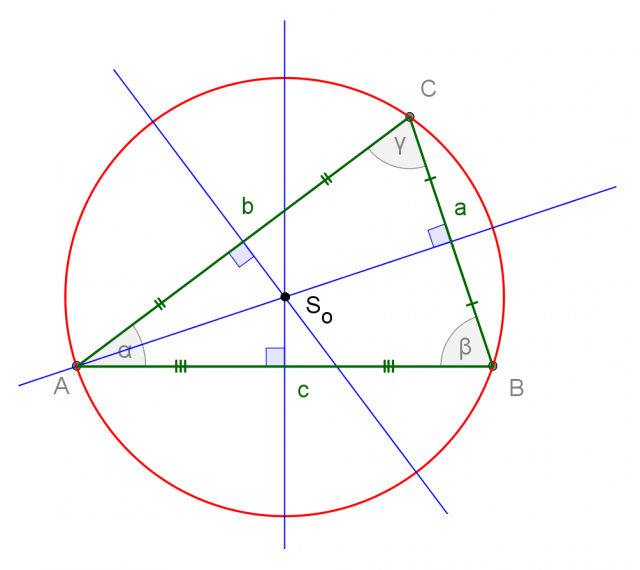
Poichè tre punti non allineati definiscono una circonferenza, ogni triangolo può essere inscritto in un cerchio.
I tre lati del triangolo sono corde della circonferenza, quindi come abbiamo visto nei paragrafi precedenti, il centro della circonferenza appartiene al loro asse di simmetria.
Triangolo inscritto in una circonferenza.
Intersecando gli assi di simmetria dei tre lati del triangolo troveremo il centro della circonferenza nella quale il triangolo è inscritto.
I vertici del triangolo risultano equidistanti dal centro così trovato.
Puntando il compasso nel centro S trovato e aprendolo con l'apertura pari alla distanza tra il centro e i vertici del triangolo, possiamo disegnare la circonferenza.
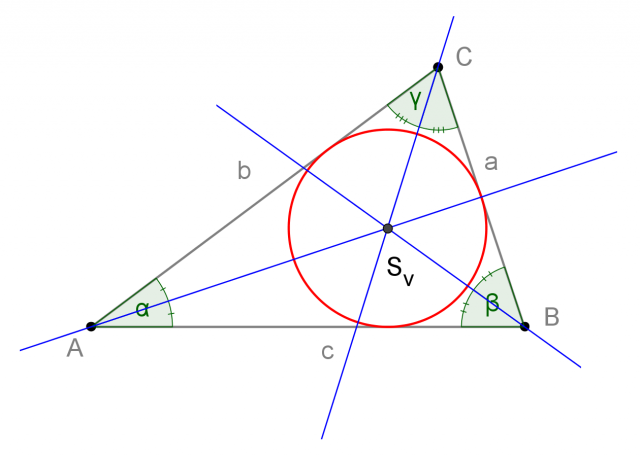
Triangolo circoscritto a una circonferenza
Come si vede dal disegno, il centro della circonferenza cui coppie di rette sono tangenti, si trova sulla bisettrice dell'angolo creato dalla coppia di rette tangenti.
Il centro della circonferenza tangente ai lati di un triangolo si trova nel punto di intersezione delle bisettrici degli angoli interni del triangolo.
Il centro della circonferenza tangente ai lati del triangolo risulterà equidistante dai lati del triangolo.
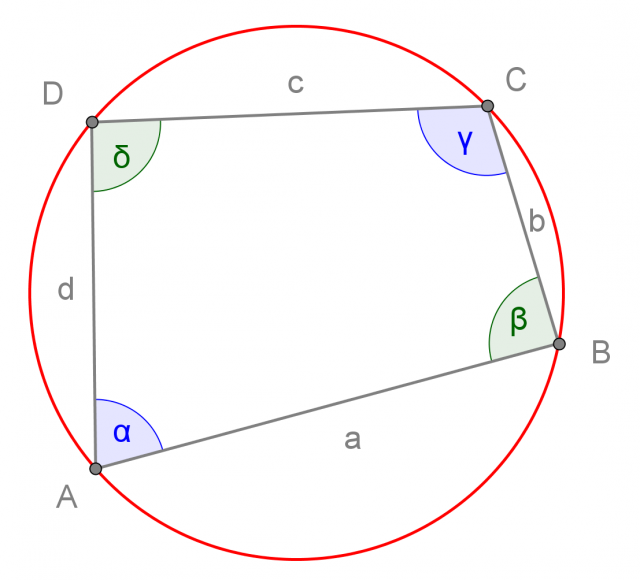
Quadrilatero inscritto in un cerchio
Dati quattro punti del piano, non è detto che esista una circonferenza che li contiene tutti e quattro. Quando questo accade, il quadrilatero che ha per vertici i quattro punti ha delle proprietà particolari, derivanti dalle proprietà delle corde e degli angoli inscritti in un cerchio.
Parleremo in questo caso di quadrilatero inscrivibile in un cerchio.
Quadrilateri inscrivibili in un cerchio.
Un quadrilatero inscrivibile in un cerchio ha gli angoli opposti supplementari:
Approfondimenti sui quadrilateri possono essere trovati nel documento sui quadrilateri.
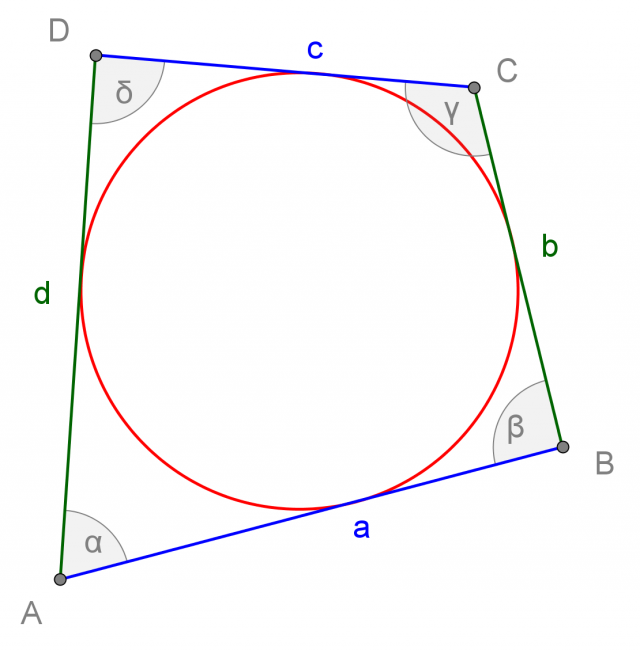
Quadrilatero circoscritto a un cerchio
Un quadrilatero è circoscritto a un cerchio quanto ha i lati tangenti al cerchio stesso:
Non tutti i quadrilateri sono circoscrivibili a un cerchio: devono infatti possedere alcune caratteristiche che rispettino le proprietà delle tangenti a una circonferenza.
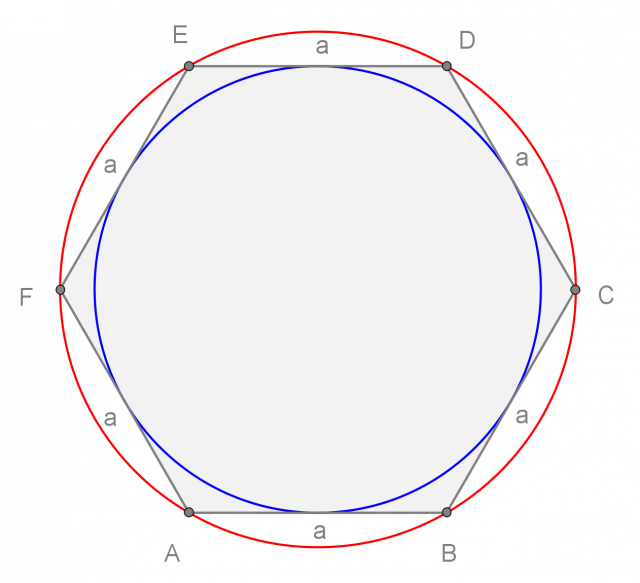
Nel quadrilatero circoscritto a un cerchio, le somme delle lunghezze delle coppie di lati opposti sono congruenti:
Approfondimenti sui quadrilateri possono essere trovati nel documento sui quadrilateri.
Relazione tra un cerchio e un poligono regolare
Poligoni con n lati possono essere inscritti o circoscritti ad un cerchio soltanto in casi particolari, per i quali non esistono regole generali se non le seguenti.
Nei poligoni inscritti, il centro si trova sull'asse di simmetria di ciascun lato. Un poligono è quindi inscrivibile solo se gli assi di simmetria di tutti i lati si intersecano in un unico punto.
Nei poligoni circoscritti, il centro si trova sulla bisettrice di ciascun angolo interno. Un poligono è quindi circoscrivibile solo se le bisettrici di tutti gli angoli interni si intersacano in un unico punto.
Alcuni poligoni particolari sono sicuramente inscrivibili e circoscrivibili a una circonferenza. Si tratta dei poligoni regolari
Un poligono regolare è un poligono con tutti i lati e tutti gli angoli interni congruenti.
Un poligono regolare è sempre inscrivibile e circoscrivibile ad una circonferenza.
Nella figura vediamo l'esempio di un esagono regolare, ovvero un poligono di 6 lati, con tutti i lati e tutti gli angoli interni congruenti tra di loro. Il cerchio in rosso è quello rispetto al quale l'esagono è inscritto, mentre il cerchio in blu è quello rispetto al quale l'esagono risulta circoscritto.




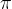 (da leggere: pi-greco), che è un
(da leggere: pi-greco), che è un 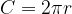
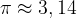
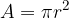
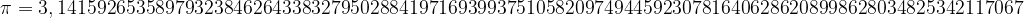
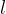 l'arco di circonferenza compreso tra i punti A e B, k l'arco complementare ad
l'arco di circonferenza compreso tra i punti A e B, k l'arco complementare ad 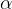 è un angolo che insiste sull'arco
è un angolo che insiste sull'arco 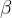 è un angolo che insiste sull'arco
è un angolo che insiste sull'arco 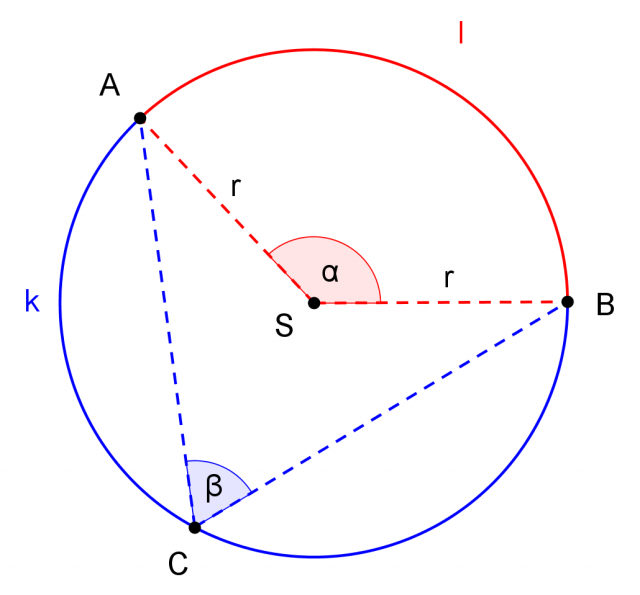
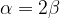
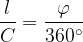
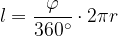
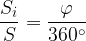
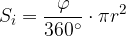
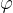 sotteso dalla stessa corda. Si sottrae l'area del triangolo isoscele ABS che ha per lati obliqui i raggi AS e BS del settore circolare e per base la corda AB (vedi immagine qui sopra).
sotteso dalla stessa corda. Si sottrae l'area del triangolo isoscele ABS che ha per lati obliqui i raggi AS e BS del settore circolare e per base la corda AB (vedi immagine qui sopra).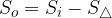
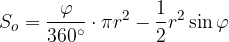
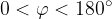
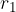 ed
ed 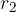 :
: