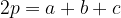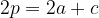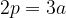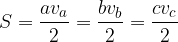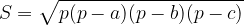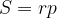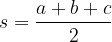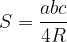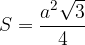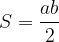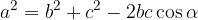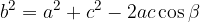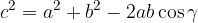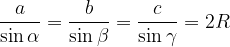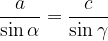Il triangolo è una figura geometrica con tre vertici e tre lati.
Indicheremo i vertici con lettere in stampatello maiuscolo (A, B, C), i lati con lettere in corsivo minuscolo (a, b, c):
I vertici del triangolo sono gli estremi non allineati dei tre lati. Per i lati del triangolo vale la disuguaglianza triangolare:
La somma delle lunghezze di due qualsiasi lati di un triangolo è maggiore della lunghezza del terzo lato:
Elementi caratteristici del triangolo
Altezza e ortocentro del triangolo
L'altezza del triangolo è la distanza tra un vertice e il lato opposto.
L'altezza del triangolo è una retta, perpendicolare ad un lato e passante per il vertice opposto.
Le tre altezze di un triangolo si incontrano in un unico punto chiamato ortocentro. Lo indichiamo con la lettera V:
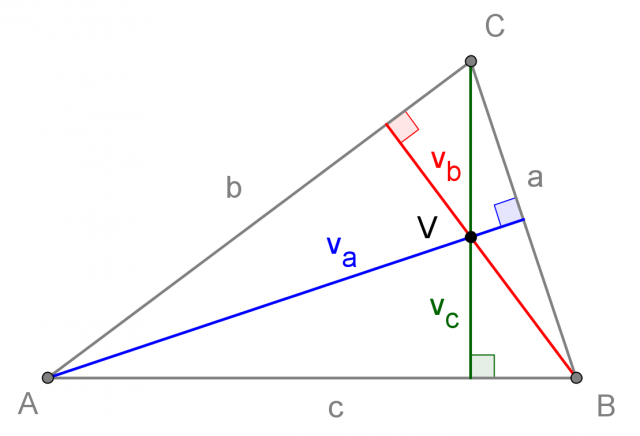
l'ortocentro del triangolo è il punto d'incontro delle altezze
Mediana e baricentro del triangolo
La mediana del triangolo è un segmento con estremi:
nel punto medio del lato opposto
Le mediane del triangolo si incontrano tutte in uno stesso punto, chiamato baricentro del triangolo. Lo indichiamo con la lettera T:
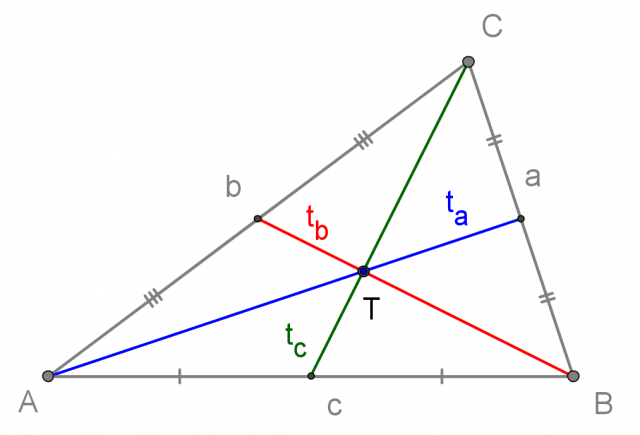
Il baricentro del triangolo è il punto d'incontro delle mediane
Angoli interni del triangolo
La somma degli angoli interni di un triangolo è di 180° (angolo piatto).
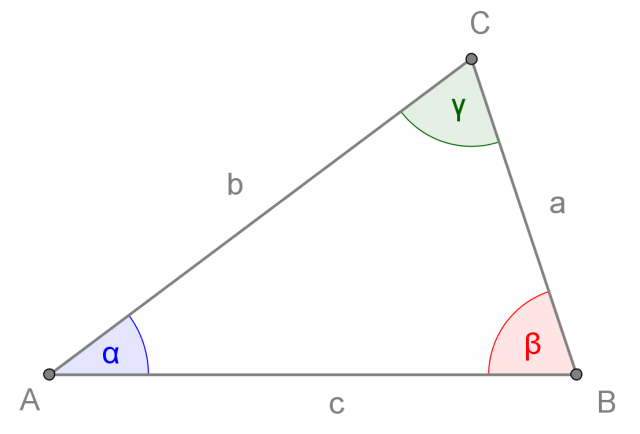
Angoli esterni di un triangolo
La somma degli angoli esterni di un triangolo è di 360° (angolo giro).
Ogni angolo esterno è pari alla somma dei due angoli interni non adiacenti:
Circonferenza circoscritta e circocentro del triangolo
Il centro della circonferenza circoscritta ad un triangolo è il punto d'intersezione degli assi di simmetria dei tre lati. Lo indichiamo con 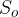 . I vertici del triangolo sono punti della circonferenza circoscritta mentre i lati del triangolo sono corde della stessa circonferenza.
. I vertici del triangolo sono punti della circonferenza circoscritta mentre i lati del triangolo sono corde della stessa circonferenza.
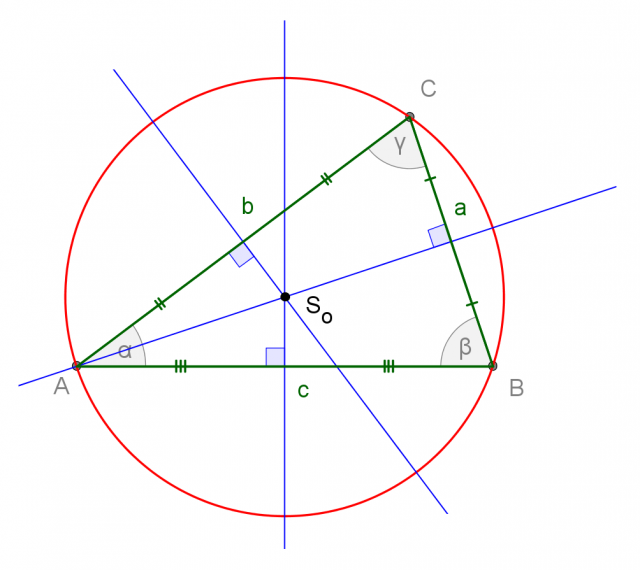
il circocentro è il punto d'intersezione degli assi di simmetria dei tre lati
Circonferenza inscritta e incentro del triangolo
Il centro della circonferenza inscritta al triangolo è il punto d'intersezione delle tre bisettrici degli angoli interni del triangolo. La indichiamo con 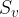 . La circonferenza inscritta è tangente ai tre lati del triangolo e si trova all'interno della figura:
. La circonferenza inscritta è tangente ai tre lati del triangolo e si trova all'interno della figura:
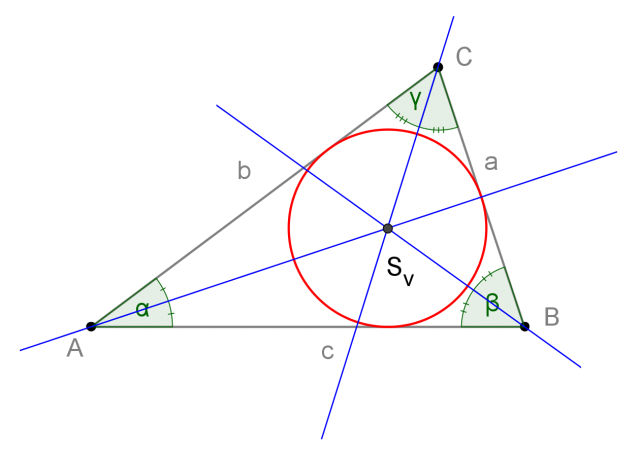
l'incentro è il punto d'incontro delle bisettrici degli angoli interni
Casi particolari di triangoli
Triangolo equilatero
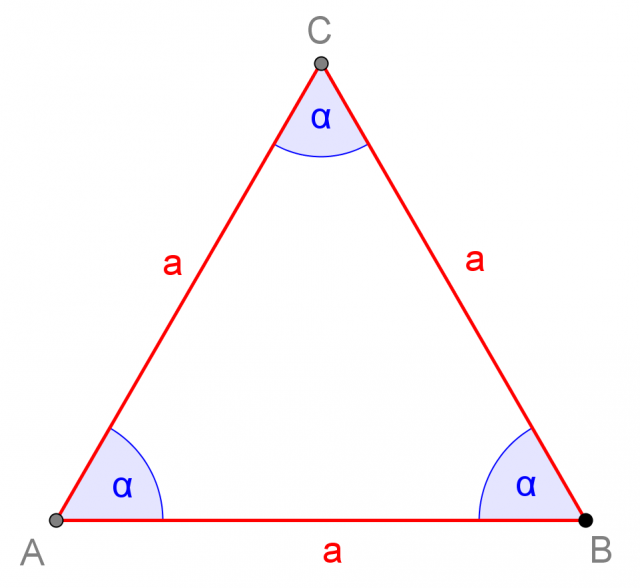
Un triangolo si dice equilatero quando ha tutti i lati congruenti e tutti gli angoli della stessa ampiezza (ovvero di 60°):
Il triangolo equilatero è un poligono regolare, in quanto ha i lati congruenti tra di loro e gli angoli interni anch'essi congruenti.
Triangolo rettangolo
E' un triangolo che ha un angolo retto (ovvero di 90°). Il lato opposto all'angolo retto è il maggiore e viene chiamato ipotenusa, mentre i due lati adiacenti all'angolo retto sono minori dell'ipotenusa e si chiamano cateti.
Valgono inoltre semplici regole per la sua risoluzione tramite le funzioni trigonometriche, illustrate nel capitolo Trigonometria.
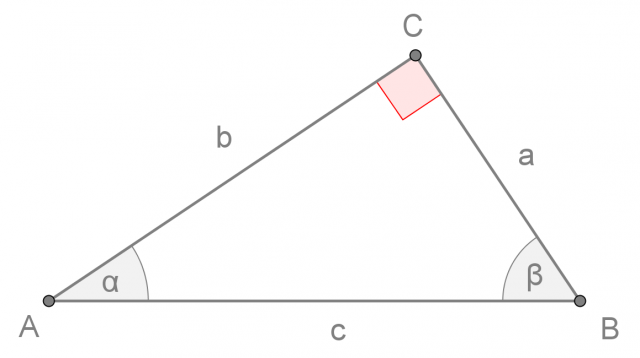
Un triangolo rettangolo di cateti a e b e di ipotenusa c
Triangolo isoscele
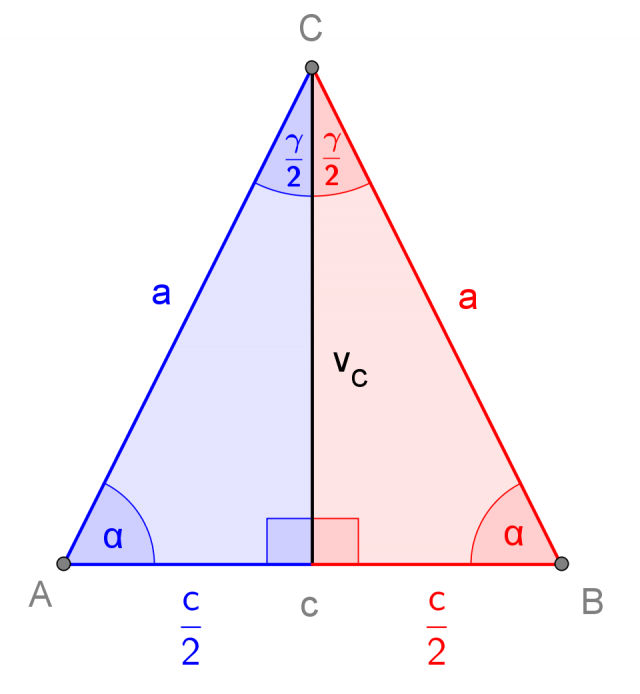
Il triangolo isoscele è caratterizzato dal fatto di avere due lati congruenti tra di loro (che chiameremo lati obliqui del triangolo). Il terzo lato viene chiamato base. Anche gli angoli opposti ai lati obliqui risultano congruenti e si dicono angoli alla base:
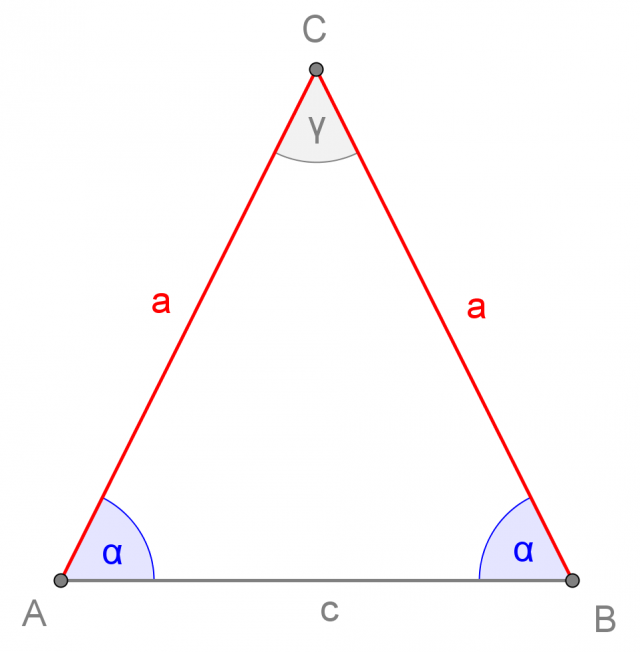
Un triangolo isoscele con lati obliqui di lunghezza a e base di lunghezza c
Se immaginiamo di dividere un triangolo isoscele lungo l'altezza 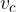 relativa alla base, otteniamo due triangoli rettangoli congruenti tra loro:
relativa alla base, otteniamo due triangoli rettangoli congruenti tra loro:
Perimetro del triangolo
Il perimetro del triangolo è dato dalla seguente formula generale:
Nei casi di triangoli particolari la formula si riscrive come segue:
Perimetro del triangolo isoscele:
Perimetro del triangolo equilatero:
Area del triangolo
L'area del triangolo è data dalla seguente formula generale:
Formula generale per calcolare l'area del triangolo:
Se non conosciamo nessuna altezza ma conosciamo tutti e 3 i lati, l'area può essere calcolata con la seguente formula:
Formula di Erone per il calcolo dell'area del triangolo:
dove con p abbiamo indicato il semiperimetro del triangolo:
Se conosciamo il raggio r della circonferenza inscritta, l'area del triangolo può essere calcolato nel modo seguente:
Area del triangolo circoscritto alla circonferenza di raggio r:
dove p indica il semiperimetro del triangolo:
L'area del triangolo inscritto alla circonferenza di raggio R è invece dato dalla seguente formula:
L'area del triangolo nei casi particolari diventa:
Area del triangolo equilatero:
Area del triangolo rettangolo:
dove a e b sono i due cateti del triangolo rettangolo.
Orientamento del triangolo
In alcuni casi può essere utile pensare al triangolo come figura "orientata", definendo una faccia positiva e una negativa tramite l'elencazione dei vertici:
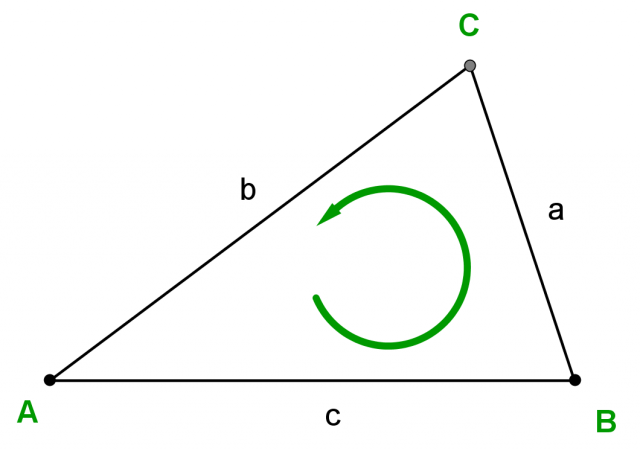
Definiamo positiva la faccia del triangolo in cui i vertici A, B e C si leggono in senso antiorario:
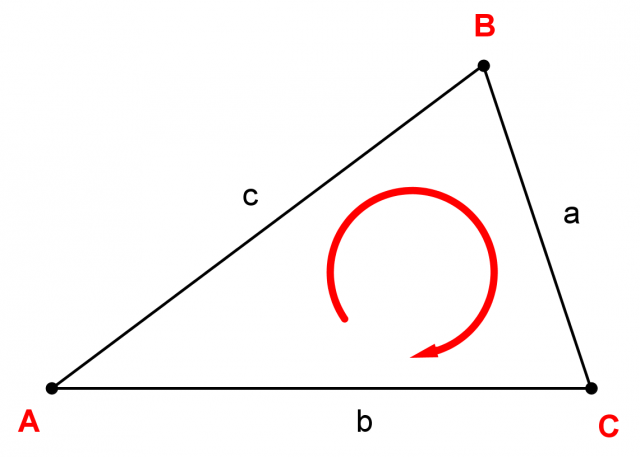
Definiamo negativa la faccia del triangolo in cui i vertici A, B e C si leggono in senso orario:
In matematica la direzione positiva non coincide con il senso orario, ma con il senso antiorario!
Il concetto di orientamento di una figura piana diventa importante in trigonometria, dove si considerano gli angoli orientati.
Teoremi sui triangoli
Descriviamo qui di seguito alcuni teoremi che permettono di calcolare lati ed angoli incogniti di un triangolo conoscendo altri lati e altri lati dello stesso triangolo. Tali procedimenti si dicono risoluzione di un triangolo.
Teorema del coseno
Il teorema del coseno è descritto dalle seguenti tre uguaglianze:
Le formule scritte qui sopra richiedono di conoscere
e permettono perciò di trovare il terzo lato.
nel caso del triangolo rettangolo, il teorema del coseno dà luogo alla formula del Teorema di Pitagora. Per questo si chiama anche "Teorema di Pitagora generalizzato". Esso è anche chiamato Teorema di Carnot, dal nome del matematico che per ultimo ne ha studiato le proprietà.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Invertendo la formula, possiamo determinare le misure degli angoli interni del triangolo conoscendo le misure dei tre lati:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Teorema dei seni
Il teorema dei seni si enuncia come segue:
In un qualunque triangolo, il rapporto tra ogni lato ed il seno dell'angolo ad esso opposto è costante, ed è pari al diametro 2R della circonferenza circoscritta:
Nella pratica l'utilizzo di questo teorema ci permette di trovare un angolo conoscendo il suo lato opposto e un'altra coppia lato-angolo opposto, oppure di trovare un lato conoscendo il suo angolo opposto e un'altra coppia lato-angolo opposto:
l'angolo opposto a uno di essi
possiamo calcolare l'angolo opposto al secondo lato.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
il lato opposto ad uno di essi
possiamo calcolare la lunghezza del lato opposto al secondo lato.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se conosciamo il raggio R della circonferenza circoscritta al triangolo possiamo:
calcolare ciascun angolo conoscendo la lunghezza del lato opposto ovvero
calcolare ciascun lato conoscendo il valore dell'angolo opposto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





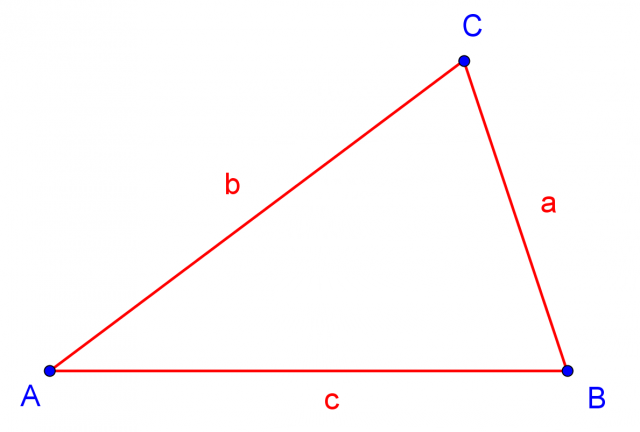
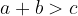
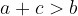
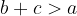
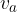 ,
, 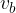 e
e 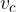 .
.
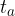 ,
, 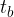 e
e 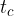 .
.
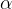 ,
, 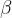 e
e 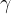 :
:
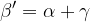
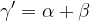
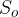 . I vertici del triangolo sono punti della circonferenza circoscritta mentre i lati del triangolo sono corde della stessa circonferenza.
. I vertici del triangolo sono punti della circonferenza circoscritta mentre i lati del triangolo sono corde della stessa circonferenza.
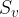 . La circonferenza inscritta è tangente ai tre lati del triangolo e si trova all'interno della figura:
. La circonferenza inscritta è tangente ai tre lati del triangolo e si trova all'interno della figura: