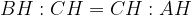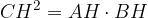I due teoremi di Euclide si applicano ai triangoli rettangoli e sono tra i teoremi più importanti della geometria euclidea.
I teoremi riguardano relazioni che si osservano quando si considera come base del triangolo rettangolo la sua ipotenusa. In questo caso l'altezza, tracciata dal vertice retto alla base, divide l'ipotenusa in due segmenti che sono le proiezioni ortogonali dei due cateti sull'ipotenusa e che chiameremo le proiezioni dei cateti sull'ipotenusa.
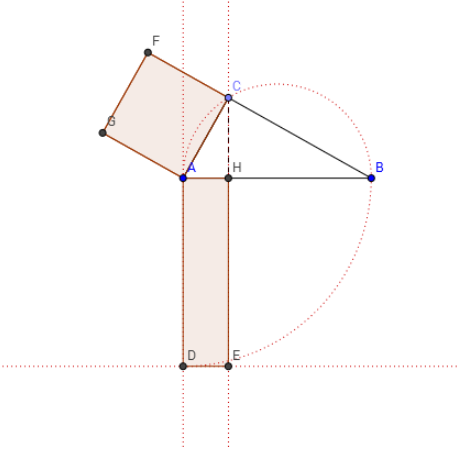
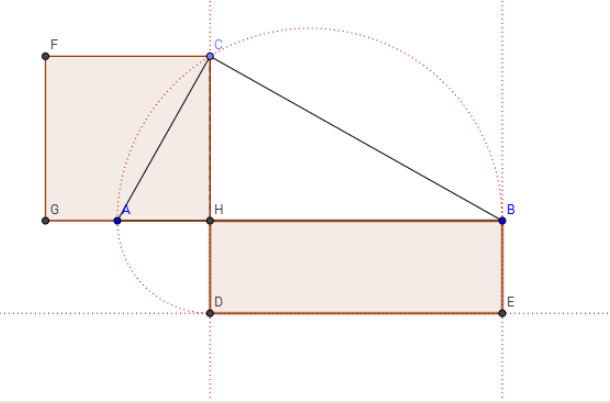
Disegniamo il triangolo rettangolo 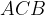 inscrivendolo nella semicirconferenza di diametro coincidente con l'ipotenusa
inscrivendolo nella semicirconferenza di diametro coincidente con l'ipotenusa 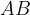 .
.
Il primo teorema di Euclide
In ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l'ipotenusa e la proiezione di quel cateto sull'ipotenusa.
In altre parole, il primo teorema di Euclide afferma che ogni cateto è medio proporzionale tra l'ipotenusa e la proiezione di quel cateto sull'ipotenusa stessa
Primo teorema di Euclide:
In ogni triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l'ipotenusa e la proiezione di quel cateto sull'ipotenusa.
Dimostrazione
Applicando la proprietà delle proporzioni (il prodotto dei medi è pari al prodotto degli estremi) si ottiene l'equivalenza voluta:
Esempi
Il primo teorema di Euclide può essere utilizzato per costruire un triangolo rettangolo di cui sono noti l'ipotenusa e la proiezione di un cateto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il secondo teorema di Euclide
Il secondo teorema di Euclide esprime una relazione tra l'altezza relativa all'ipotenusa e i due segmenti in cui essa taglia l'ipotenusa stessa (ovvero le proiezioni dei cateti sull'ipotenusa):
Il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le due proiezioni dei cateti sull'ipotenusa.
L'altezza relativa all'ipotenusa è media proporzionale tra le proiezioni dei due cateti.
Secondo teorema di Euclide:
Il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull'ipotenusa.
Dimostrazione
Anche il secondo teorema di Euclide si dimostra facilmente applicando la similitudine dei triangoli:, la dimostrazione del primo teorema di Euclide è immediata.
Nel triangolo BCH, l'altezza CH è il cateto omologo al cateto minore del triangolo ABC e la proiezione HB è il cateto omologo al cateto maggiore del triangolo ABC.
Nel triangolo ACH invece, l'altezza CH è il cateto omologo al cateto maggiore di ABC mentre la proiezione AH è omologa al cateto minore di ABC.
Scriveremo quindi la proporzione in questo modo
Applicando la proprietà delle proporzioni (il prodotto dei medi è pari al prodotto degli estremi) si ottiene l'equivalenza voluta:
Esempi
Il secondo teorema di Euclide ha molte interessanti applicazioni: può ad esempio essere usato per costruire un segmento di lunghezza pari alla radice quadrata di un numero a piacere.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




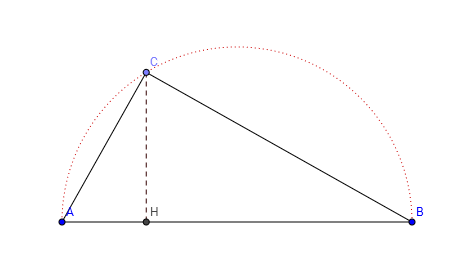
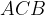 inscrivendolo nella semicirconferenza di diametro coincidente con l'ipotenusa
inscrivendolo nella semicirconferenza di diametro coincidente con l'ipotenusa 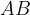 .
.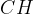 si dice altezza relativa all'ipotenusa. Il segmento
si dice altezza relativa all'ipotenusa. Il segmento 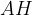 e il segmento
e il segmento 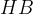 in cui risulta suddivisa l'ipotenusa sono le proiezioni dei cateti sull'ipotenusa.
in cui risulta suddivisa l'ipotenusa sono le proiezioni dei cateti sull'ipotenusa.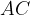 sull'ipotenusa e
sull'ipotenusa e 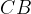 sull'ipotenusa.
sull'ipotenusa.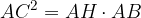
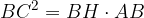
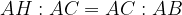
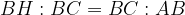
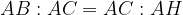
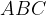 e il triangolo
e il triangolo 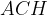 . Essi sono simili in quanto entrambi hanno un
. Essi sono simili in quanto entrambi hanno un  in comune. Gli elementi corrispondenti di ciascun triangolo sono quindi in proporzione tra di loro.
in comune. Gli elementi corrispondenti di ciascun triangolo sono quindi in proporzione tra di loro.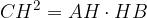
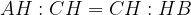
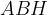 e il triangolo
e il triangolo