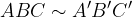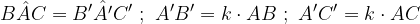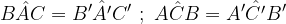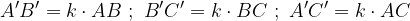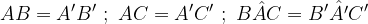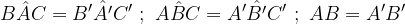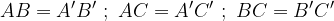Nel linguaggio comune utilizziamo l'aggettivo simili per indicare due cose che abbiano in comune alcune caratteristiche essenziali: ad esempio, se un genitore e un figlio hanno gli stessi lineamenti, diremo che si assomigliano o che i loro volti sono simili. In biologia, chiameremo simili tutti gli esseri appartenenti ad una stessa specie.
In matematica, l'aggettivo simili ha un significato più preciso, che si applica alle figure geometriche: diciamo che due figure sono simili se esiste una trasformazione lineare che permette di passare da una all'altra, conservandone la forma e le proporzioni. In questo caso parliamo di similitudine tra le figure.
Un caso particolare di similitudine è quello in cui la trasformazione è isometrica, ovvero conserva non solo la forma e le proporzioni ma anche le misure. In questo caso parliamo allora di congruenza tra le figure.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In questo capitolo studieremo la similitudine e la congruenza dei triangoli, che sono le figure geometriche più basilari. Per studiare le similitudini utilizzeremo i concetti di rapporto e proporzione.
Similitudine di figure geometriche
Riassumendo quanto visto finora possiamo dire che:
Figure geometriche simili hanno la stessa forma ma diverse dimensioni.
Figure geometriche congruenti hanno la stessa forma e dimensione.
La similitudine è una trasformazione lineare. Questo significa che il rapporto tra le dimensioni degli elementi corrispondenti di figure simili è costante.
il rapporto tra un qualunque segmento appartenente alla figura e la sua immagine è pari ad una costante 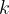 che chiamiamo coefficiente di proporzionalità.
che chiamiamo coefficiente di proporzionalità.
il rapporto tra una qualunque area appartenente alla figura e l'area della sua immagine è pari al quadrato del coefficiente di proporzionalità, ovvero è pari a 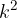 .
.
Vediamo il caso di un triangolo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il coefficiente 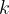 esprime la proporzionalità che si verifica tra qualunque segmento appartenente alla figura e la sua immagine.
esprime la proporzionalità che si verifica tra qualunque segmento appartenente alla figura e la sua immagine.
In particolare quindi esprime anche:
il rapporto tra le altezze
il rapporto tra mediane, bisettrici e corde corrispondenti
Nel prossimo esempio vedremo che il coefficiente 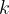 esprime anche il rapporto tra i perimetri di figure simili:
esprime anche il rapporto tra i perimetri di figure simili:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criteri di similitudine dei triangoli
Il triangolo è il poligono più semplice, e ogni poligono può essere scomposto in triangoli: possiamo quindi chiederci se ci sono regole semplici per stabilire se due triangoli sono simili:
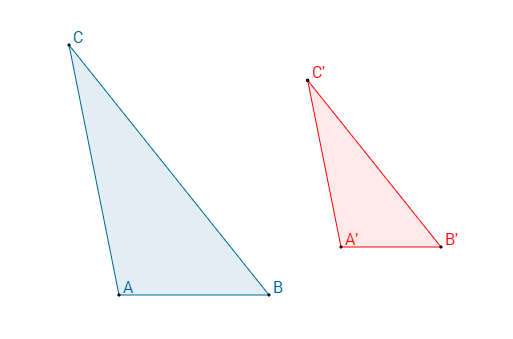
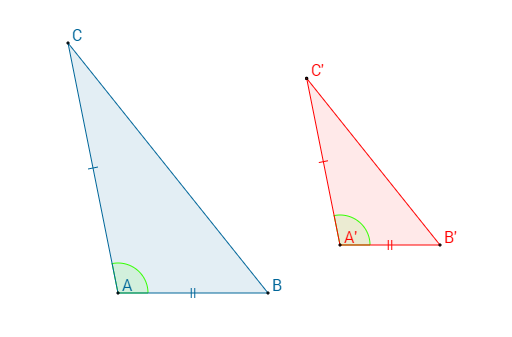
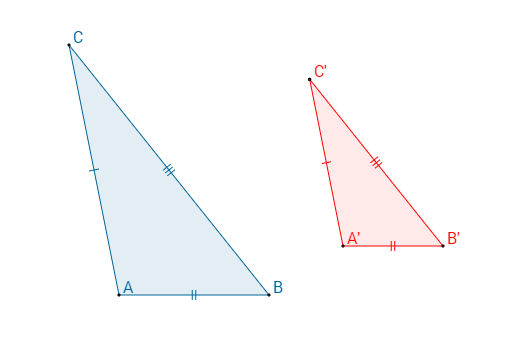
La similitudine di due triangoli ABC e A'B'C' si può esprimere in formule in questo modo:
Prima di ricercare dei criteri di similitudine, osserviamo che:
Due triangoli sono simili se e solo se:
il rapporto tra i lati corrispondenti è costante
gli angoli corrispondenti nella trasformazione sono congruenti (ovvero hanno la stessa ampiezza)
In base a queste due condizioni, dovremmo verificare l'uguaglianza di tre rapporti tra i lati e la congruenza di tre angoli.
In particolare ricordiamo le seguenti proprietà che utilizzeremo:
Somma degli angoli interni di un triangolo
La somma degli angoli interni di un qualunque triangolo è di 180°
Teorema di Talete applicato ai triangoli
Una retta parallela al lato di un triangolo taglia gli altri due lati in segmenti proporzionali tra di loro.
Se una retta determina su due lati di un triangolo segmenti proporzionali, allora è parallela al terzo lato.
Grazie a queste due proprietà, possiamo individuare tre criteri di similitudine dei triangoli:
Primo criterio di similitudine dei triangoli
Due triangoli sono simili se e solo se hanno un angolo congruente e i due lati ad esso adiacenti proporzionali tra di loro secondo una stessa costante k
La dimostrazione di questo criterio è riportata per esteso negli esercizi.
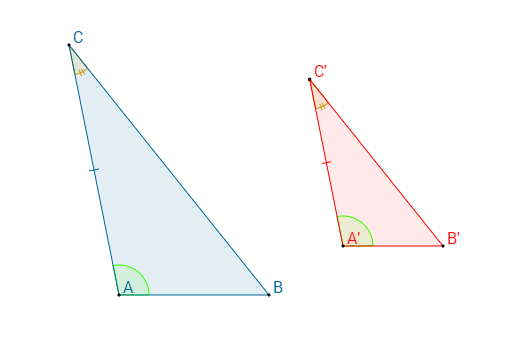
Secondo criterio di similitudine dei triangoli
Due triangoli sono simili se e solo se hanno due angoli congruenti. Il coefficiente di proporzionalità k è dato allora dal rapporto tra le misure dei lati di ciascun triangolo che i due angoli congruenti hanno in comune.
La dimostrazione di questo criterio è riportata per esteso negli esercizi.
Terzo criterio di similitudine dei triangoli
Due triangoli sono simili se e solo se hanno i tre lati a due a due proporzionali tra di loro secondo una stessa costante k.
La dimostrazione è riportata per esteso negli esercizi.
Congruenza di figure geometriche
Come abbiamo visto nel capitolo Trasformazioni lineari nel piano, l'uguaglianza di due figure geometriche, o meglio, per usare un linguaggio corretto, la loro congruenza, può essere considerata un caso particolare di trasformazione lineare dove il coefficiente k di proporzionalità sia tale che
Analogamente a quanto visto prima per le similitudini, potremmo quindi dire che nel caso di due figure congruenti:
la lunghezza di un segmento e quella del suo segmento immagine sono uguali
l'area della figura origine e l'area della sua immagine sono uguali
Nel caso dei triangoli, possiamo individuare nuovamente tre criteri di congruenza che derivano direttamente dai rispettivi criteri di similitudine:
Criteri di congruenza dei triangoli
Applicando a quanto visto per la similitudine la condizione |k| = 1, possiamo formulare la congruenza dei triangoli nel modo seguente:
Due triangoli sono congruenti se e solo se:
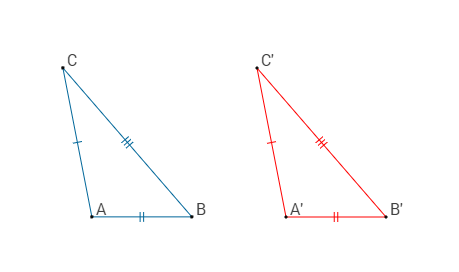
tutti i lati sono congruenti
gli angoli corrispondenti nella trasformazione sono congruenti
Riprendendo i criteri di similitudine visti nei paragrafi precedenti, possiamo allora formulare i seguenti tre criteri di congruenza dei triangoli, la cui dimostrazione si ottiene applicando il rispettivo criterio di similitudine con la condizione |k| = 1:
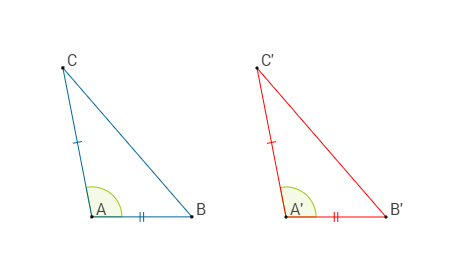
Primo criterio di congruenza dei triangoli
Ricordando il primo criterio di similitudine dei triangoli e applicando la condizione |k| = 1 possiamo scrivere che:
Due triangoli sono congruenti se e solo se hanno un angolo congruente e i due lati ad esso adiacenti congruenti.
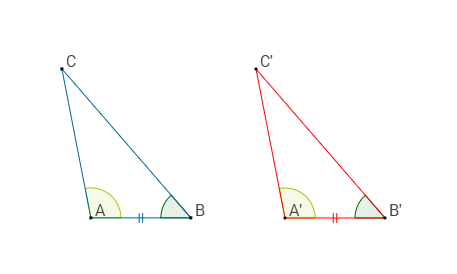
Secondo criterio di congruenza dei triangoli
Ricordando il secondo criterio di similitudine dei triangoli e applicando la condizione |k| = 1 possiamo scrivere che:
Due triangoli sono congruenti se e solo se hanno due angoli e il lato tra essi compreso congruenti.
Terzo criterio di congruenza dei triangoli
Applicando la condizione |k| = 1 al terzo criterio di similitudine, otteniamo infine che:
Due triangoli sono congruenti se e solo se hanno tutti i lati congruenti.




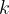 che chiamiamo coefficiente di proporzionalità.
che chiamiamo coefficiente di proporzionalità.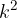 .
.