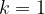Che cosa intendiamo per trasformazione nel piano?
Intuitivamente, possiamo dire che una trasformazione è una regola che permette di passare da una forma geometrica ad un'altra.
In linguaggio matematico, possiamo chiamare con X la forma di partenza e Y la forma di arrivo della trasformazione. Scriveremo quindi:
per indicare una regola che trasforma X in Y.
Definizioni
Per poter studiare le trasformazioni geometriche, definiamo alcuni termini che useremo per descriverle:
la figura di partenza si chiama figura origine; un elemento (punto) della figura origine si chiama elemento (punto) origine;
la figura trasformata si chiama immagine o mappa della trasformazione; un elemento (punto) della figura immagine si chiama elemento (punto) immagine.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà delle trasformazioni lineari
Il concetto di trasformazione è molto ampio. Le trasformazioni che si studiano nella geometria piana sono quelle che:
mantengono il parallelismo tra le rette
mantengono gli angoli tra le rette
mantengono le distanze tra i punti
Le trasformazioni che rispettano la condizione (i) ma non necessariamente le altre due si chiamano trasformazioni affini e non si studiano nella geometria elementare.
Le trasformazioni che rispettano almeno le condizioni (i) e (ii) si chiamano trasformazioni lineari e sono l'oggetto di questo capitolo. Cerchiamo di capire di che cosa si tratta.
Le proprietà (i) e (ii) scritte sopra ci permettono di definire una trasformazione lineare come una trasformazione che mantiene la forma della figura. La proprietà (iii) invece definisce ogni trasformazione che mantenga le dimensioni, ovvero la grandezza, della figura. Questa proprietà è indipendente dalle prime due.
A seconda che valga o no la proprietà (iii) possiamo allora distinguere le trasformazioni lineari in due categorie:
trasformazioni che mantengono soltanto la forma ma non le dimensioni
trasformazioni che mantengono sia la forma sia le dimensioni
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Studiando le trasformazioni lineari, si trova che esse sono sempre una combinazione di alcuni tipi particolari di trasformazione, che verranno approfondite ciascuna in un apposito capitolo:
Di esse, soltanto la trasformazione (I), ovvero l'omotetìa, non mantiene le dimensioni, mentre le trasformazioni (II)-(IV) mantengono sia la forma sia le dimensioni della figura e vengono anche chiamate Isometrie del piano.
Definizione algebrica delle trasformazioni lineari
Abbiamo visto che le trasformazioni lineari si possono distinguere in due diversi tipi, apparentemente molto diversi tra di loro in quanto in un caso la trasformazione non mantiene le dimensioni della figura, mentre nell’altro caso le mantiene.
Dal punto di vista matematico, questi due casi si possono riassumere in un'unica definizione. Per questo si possono riunire in un’unica categoria: quella delle trasformazioni lineari.
Una trasformazione lineare è una trasformazione tale che, se A e B sono due qualunque punti della figura origine e A' e B' le loro immagini nella trasformazione, risulta:
dove 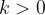 è una costante, ovvero un coefficiente indipendente dalla scelta dei punti A e B, che si dice costante di proporzionalità della trasformazione.
è una costante, ovvero un coefficiente indipendente dalla scelta dei punti A e B, che si dice costante di proporzionalità della trasformazione.
La definizione (2) scritta sopra dice che il rapporto tra la distanza dei punti di partenza e la distanza delle loro immagini nell'insieme d'arrivo è costante, pari al coefficiente k di proporzionalità della trasformazione.
Classificazione algebrica delle trasformazioni lineari
A seconda del valore del coefficiente k, possiamo distinguere i diversi tipi di trasformazioni lineari:
per 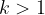 (dilatazioni)
(dilatazioni)
per  (contrazioni)
(contrazioni)
Le omotetie mantengono la forma ma non le dimensioni.
per 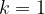
Le isometrie mantengono sia la forma sia le dimensioni della figura.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




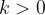 è una costante, ovvero un coefficiente indipendente dalla scelta dei punti A e B, che si dice costante di proporzionalità della trasformazione.
è una costante, ovvero un coefficiente indipendente dalla scelta dei punti A e B, che si dice costante di proporzionalità della trasformazione.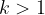 (dilatazioni)
(dilatazioni) (contrazioni)
(contrazioni)