Nel capitolo Isometrie nel piano abbiamo definito una simmetria assiale 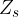 rispetto ad una retta s come un'isometria che
rispetto ad una retta s come un'isometria che
ribalta l'orientazione della figura (ad esempio se i vertici della figura origine sono ordinati in senso antiorario, le loro immagini risultano ordinate in senso orario)
ha come punti fissi i punti dell'asse di simmetria s.
Abbiamo quindi dato la definizione di simmetria assiale in questo modo:
Data una retta  del piano, l'isometria
del piano, l'isometria
è una simmetria assiale se e solo se ha le seguenti proprietà:
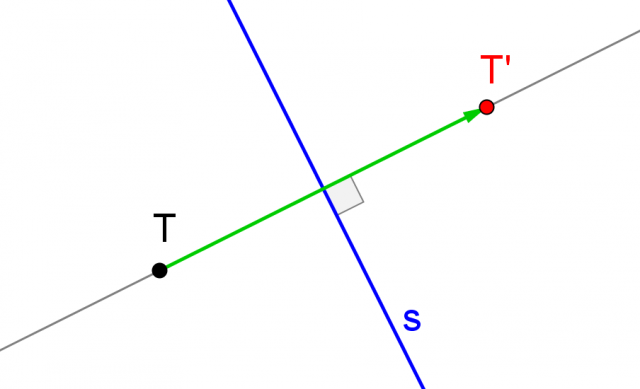
il segmento TT' è perpendicolare ad 
La distanza di  dal punto T' è pari alla distanza di
dal punto T' è pari alla distanza di  dal punto T
dal punto T
Costruire una simmetria assiale
Quando ci guardiamo allo specchio, l'impressione che abbiamo è che la nostra immagine riflessa abbia la stessa distanza dalla superficie dello specchio come quella che abbiamo noi. Anche gli altri oggetti attorno a noi ci sembrano riflessi alla stessa distanza dallo specchio come quella che hanno nella realtà.
Per costruire una simmetria assiale nel piano bisogna quindi collocare l'immagine di ogni punto alla stessa distanza dall'asse di simmetria come quella del punto considerato, ma dall'altra parte della retta ovvero, per usare i termini matematici, nel semipiano opposto.
Trovare l'asse di una simmetria
Supponiamo di avere due figure isometriche che non hanno la stessa orientazione: come possiamo sapere se sono una la simmetrica dell'altra rispetto ad una simmetria assiale?
La nostra definizione di simmetria assiale prevede che:
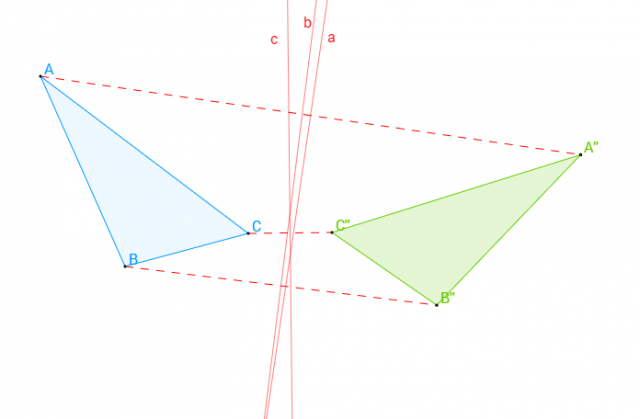
l'asse di simmetria sia perpendicolare al segmento che congiunge ciascun punto con la sua immagine
l'asse di simmetria passi nel punto medio tra ciascun punto e la sua immagine
In definitiva l'asse di simmetria dev'essere l'asse di ogni segmento che congiunge un punto con la sua immagine.
Questo vuol dire che ciascuno dei segmenti così costruiti dev'essere parallelo a tutti gli altri, in quanto devono essere tutti perpendicolari alla stessa retta. I loro punti medi inoltre devono essere tutti allineati.
Se questo avviene, per trovare l'asse di simmetria basterà costruire l'asse del segmento che congiunge un qualsiasi punto della figura origine con il suo punto corrispondente nella figura immagine.
Nel caso dei poligoni, è sufficiente lavorare ad esempio sui vertici. Vediamo il caso dei triangoli con qualche esempio.
La prima cosa da fare, è di congiungere ciascun vertice con la sua immagine. Otterremo così tre segmenti e osservando le loro posizioni reciproche possiamo distinguere due diversi casi:
i tre segmenti sono tutti paralleli tra di loro
i tre segmenti non sono tutti paralleli tra di loro
Vediamo cosa succede in ciascuno dei due casi:
Caso 1: I segmenti che congiungono ogni vertice con la sua immagine sono tutti paralleli tra di loro
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Caso 2: i segmenti che congiungono ogni vertice con la sua immagine non sono tutti paralleli tra di loro
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Glissosimmetrie
Consideriamo un'isometria inversa che non sia una semplice simmetria:
Gli assi dei segmenti che congiungono i vertici corrispondenti non sono paralleli tra di loro, quindi l'isometria non è una simmetria assiale. Questo secondo tipo di isometria inversa può essere pensato come la composizione di una traslazione e di una simmetria assiale, per questo prende il nome di glissosimmetria o di antitraslazione.
Figure invarianti per simmetria assiale
Se prendiamo carta e forbici e ritagliamo alcune figure, possiamo notare che:
alcune figure si possono piegare a metà in modo che le due parti si sovrappongano esattamente, seguendo alcune linee di piegatura particolari
alcune figure non si possono mai piegare a metà in modo che le due parti si sovrappongano esattamente, qualunque sia la linea di piegatura che scegliamo
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le simmetrie assiali possono essere usate per classificare alcune figure:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In generale, indicando con n un numero intero maggiore o uguale a zero, possiamo dire che:
Una figura geometrica ha n assi di simmetria se esistono n corde distinte rispetto alle quali una simmetria assiale trasforma la figura in se stessa.
Se n = 0, la figura non ha assi di simmetria.
Se n > 0 si può dire che la figura ha n assi di simmetria.
Tutte le isometrie nascono dalle simmetrie assiali
Un risultato interessante che si dimostra nella matematica avanzata è il seguente:
tutte le isometrie del piano possono essere generate da una composizione di una, due o tre simmetrie assiali opportunamente scelte
Naturalmente, se si applica una sola simmetria assiale si ottiene ... proprio quella simmetria assiale!
Possiamo quindi immaginare che le traslazioni, le rotazioni e le glissosimmetrie (e persino l'identità, ovvero l'isometria che lascia immobile la figura) vengano generate da due o più simmetrie assiali.
Per verificare con qualche esempio intuitivo questo sorprendente risultato, verifichiamolo con qualche esempio nei seguenti casi:
identità (2 simmetrie assiali)
traslazione (2 simmetrie assiali)
rotazione (2 simmetrie assiali)
La glissosimmetria è una composizione di una traslazione e di una simmetria assiale, quindi le simmetrie assiali necessarie per generarla saranno 2 + 1 = 3.
Identità
Ricordiamo che l'isometria identica o identità è quella isometria che manda ogni punto in se stesso.
Possiamo dire con parole semplici che l'isometria identica è quella che lascia "immobile" la figura.
l'isometria identica può essere ottenuta applicando due volte la simmetria assiale rispetto a uno stesso asse di simmetria scelto a piacere.
Vediamolo con un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Traslazione
Ricordiamo che una traslazione è definita da un vettore costante che definisce il modulo, la direzione e il verso della traslazione per ciascun punto dell'insieme a cui è applicata.
Vediamo con un esempio come si può ottenere una traslazione applicando consecutivamente due simmetrie assiali:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Rotazione
Ricordiamo che una rotazione è definita da un punto fisso (il centro della rotazione) e da un angolo di rotazione che è costante per tutti i punti.
Vediamo con un esempio come la rotazione può essere ottenuta applicando consecutivamente due simmetrie assiali:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il modo in cui possiamo scegliere i due assi di simmetria non è unico, tuttavia possiamo intuire (e si può dimostrare) la seguente proprietà degli assi di simmetria che compongono una rotazione:
Una rotazione di centro C e angolo 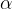 si può scomporre in due simmetrie assiali con gli assi passanti per il punto C e tali che l'angolo da essi formato sia pari alla metà di
si può scomporre in due simmetrie assiali con gli assi passanti per il punto C e tali che l'angolo da essi formato sia pari alla metà di 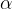


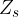 rispetto ad una retta s come un'isometria che
rispetto ad una retta s come un'isometria che del piano, l'isometria
del piano, l'isometria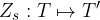
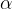 si può scomporre in due simmetrie assiali con gli assi passanti per il punto C e tali che l'angolo da essi formato sia pari alla metà di
si può scomporre in due simmetrie assiali con gli assi passanti per il punto C e tali che l'angolo da essi formato sia pari alla metà di 


