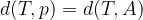Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti


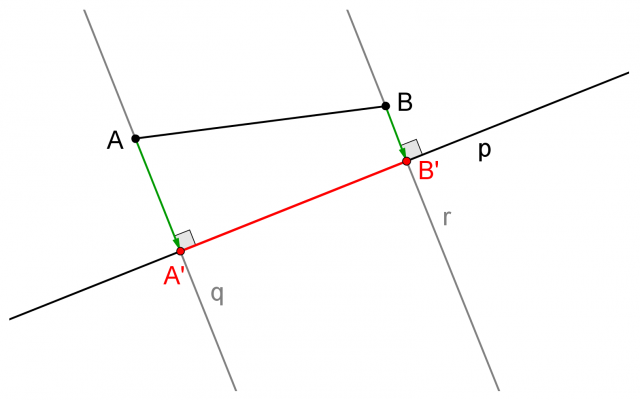
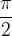 se esprimiamo la misura in radianti):
se esprimiamo la misura in radianti):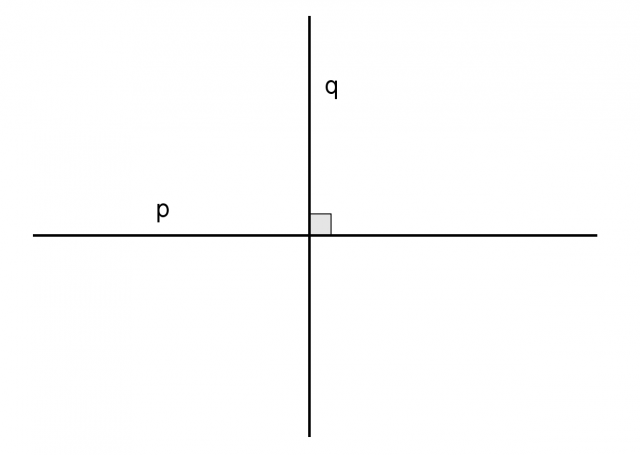
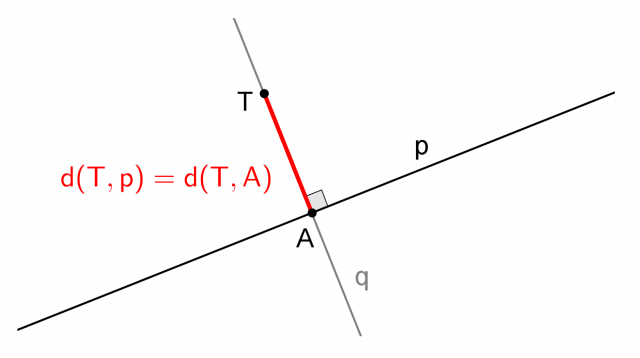
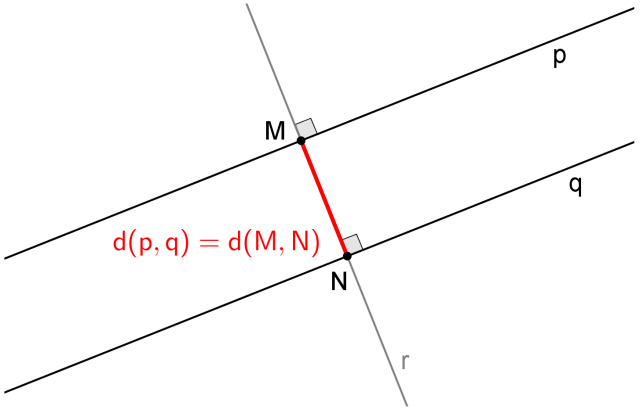
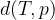 la distanza tra il punto T e la retta p e con
la distanza tra il punto T e la retta p e con 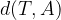 la lunghezza del segmento TA.
la lunghezza del segmento TA.