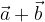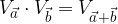Nel capitolo Isometrie nel piano abbiamo definito una traslazione come uno spostamento rigido di tutti i punti della figura in una stessa direzione per una determinata lunghezza.
Utilizzando i vettori abbiamo quindi definito la traslazione in questo modo:
Una traslazione è una trasformazione del piano caratterizzata da un vettore 
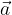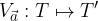
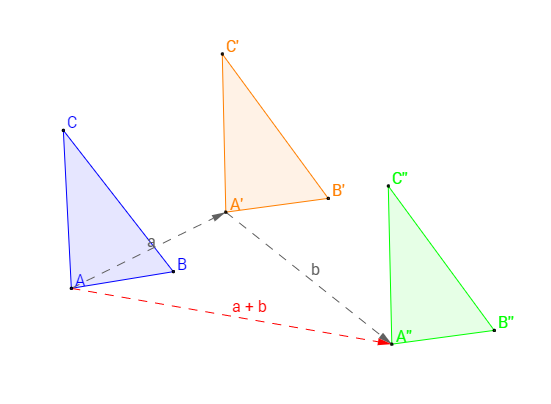
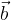tale che ad ogni punto T dell'insieme origine corrisponde il punto immagine T' ottenuto applicando a T. In formule:
Abbiamo visto che una traslazione ha le seguenti proprietà:
A ogni punto al quale viene applicato il vettore nell'insieme di partenza corrisponde uno ed un solo punto immagine nell'insieme di arrivo e viceversa (è una corrispondenza biunivoca)
Conserva l'inclinazione di ogni linea rispetto a un riferimento fisso
Mantiene invariate le misure degli angoli (è una trasformazione lineare)
Mantiene invariate le distanze tra i punti (è una isometria)
Mantiene l' orientazione
Vediamo ora alcuni approfondimenti e qualche esempio di traslazioni.
Ci possiamo chiedere cosa succede se applichiamo una dopo l'altra due traslazioni allo stesso oggetto. Avremo ancora una traslazione?
Aiutiamoci con una figura per capire cosa succede:
Applicando successivamente al triangolo ABC le traslazioni di vettore e 
otteniamo la stessa traslazione che avremmo applicando il vettore somma 
Se applichiamo una dopo l'altra due traslazioni, avremo fatto due movimenti rigidi che mantengono la forma e le dimensioni della figura, la sua orientazione e l'inclinazione rispetto ad un riferimento fisso.
Se confrontiamo la figura di partenza e quella di arrivo dopo le due traslazioni successive, anch'esse avranno quindi la stessa forma e dimensione, la stessa orientazione e la stessa inclinazione rispetto ad un riferimento fisso.
Possiamo quindi dire che:
Applicando successivamente due traslazioni otteniamo ancora una traslazione.
Ricordando le regole per la somma di due vettori, possiamo precisare ancora meglio la definizione della composizione di due traslazioni osservando che:
Il vettore della nuova traslazione ottenuta componendo due traslazioni successive, è il vettore somma ottenuto sommando i vettori delle due traslazioni di partenza.
In formule:
Molti motivi ornamentali sono ottenuti a partire da una figura base che viene ripetutamente traslata di uno stesso vettore. Alcuni tipi di "cornicette" con figure ripetute senza ribaltamenti ne sono un esempio:
Se osserviamo ad esempio le piastrelle di un pavimento, possiamo trovare altri esempi di figure ripetute che si possono sovrapporre su se stesse attraverso una o più traslazioni. Nel caso delle pavimentazioni, l'intera figura viene generata a partire dalla figura base attraverso due distinte traslazioni non parallele tra di loro.
