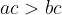L'insieme dei numeri reali è l'insieme di tutti i numeri con decimali illimitati.
I numeri decimali illimitati sono i numeri la cui parte decimale ha infinite cifre. E' importante notare che tra questi è possibile includere, come caso particolare, anche i numeri interi se li consideriamo formati da una parte decimale costituita da zeri infiniti.
L'insieme dei numeri reali
L'insieme dei numeri reali è costituito dai seguenti sottoinsiemi:
insieme dei numeri razionali
insieme dei numeri irrazionali
Diamo una definizione di questi due insiemi:
Numeri razionali
I numeri razionali sono i numeri che possono essere scritti sotto forma di frazione. L'insieme dei numeri razionali viene indicato con il simbolo 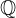
Numeri irrazionali
I numeri irrazionali sono, per definizione, tutti i numeri reali che non possono essere scritti sotto forma di frazione. Sono numeri irrazionali, ad esempio, tutte le radici quadrate di numeri interi positivi che non sono quadrati perfetti, tutte le radici cubiche di numeri interi che non sono cubi perfetti, ecc.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'insieme dei numeri irrazionali è un insieme infinito.
Tra due numeri razionali qualsiasi ci sono infiniti numeri razionali ed infiniti numeri irrazionali.
Da questo presupposto possiamo introdurre l'insieme dei numeri reali:
I numeri reali
Se l'insieme dei numeri razionali viene esteso in modo da includere anche i numeri irrazionali, otteniamo un nuovo insieme, denominato insieme dei numeri reali.
Si presume che ogni numero reale corrisponde ad un punto su una retta, detta retta reale (o retta numerica), e che, viceversa, ogni punto sulla retta reale sia rappresentativo di un numero reale. Esiste quindi una corrispondenza biunivoca tra i numeri reali e i punti della retta.
Per gli insiemi numerici vale la seguente gerarchia:
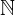 ... insieme dei numeri naturali
... insieme dei numeri naturali
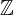 ... insieme dei numeri interi
... insieme dei numeri interi
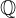 ... insieme dei numeri razionali
... insieme dei numeri razionali
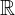 ... insieme dei numeri reali
... insieme dei numeri reali
Per comprendere meglio tale gerarchia, consideriamo la seguente rappresentazione grafica:
Qui di seguito vedremo le operazioni aritmetiche che si possono compiere sull'insieme dei numeri reali:
Operazioni aritmetiche
Nell'insieme dei numeri reali si possono compiere le seguenti operazioni aritmetiche:
tenendo presenti le seguenti proprietà:
Proprietà delle operazioni aritmetiche fondamentali
Considerati tre numeri reali arbitrari a, b e c, vale:
Proprietà commutativa dell'addizione:
Proprietà associativa dell'addizione:
0 è un elemento neutro per l'addizione:
Proprietà commutativa della moltiplicazione:
Proprietà associativa della moltiplicazione:
1 è l'elemento neutro per la moltiplicazione:
Proprietà distributiva della moltiplicazione
moltiplicazione di numeri inversi:
Vediamo ora più nel dettaglio la divisione di numeri reali:
Divisione di numeri reali
La divisione di numeri reali può essere definita nel seguente modo:
Siano a e c due numeri reali arbitrari e b un numero reale arbitrario diverso da zero, l'operazione di divisione può essere scritta in uno dei seguenti modi:
Da ciò possiamo evincere che esiste una relazione di equivalenza tra moltiplicazione e divisione:
Per l'operazione di divisione di numeri numeri reali valgono le seguenti proprietà:
Sottoinsiemi dei numeri reali
L'insieme dei numeri reali può essere considerato come l'unione dei seguenti sottoinsiemi disgiunti:
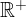 ... insieme dei numeri reali positivi
... insieme dei numeri reali positivi
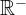 ... insieme dei numeri reali negativi
... insieme dei numeri reali negativi
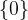 ... insieme contenente il numero zero
... insieme contenente il numero zero
L'unione dei tre insiemi si può rappresentare nel seguente modo:
Come abbiamo visto precedentemente, i numeri reali possono essere rappresentati su una retta numerica:
La retta numerica
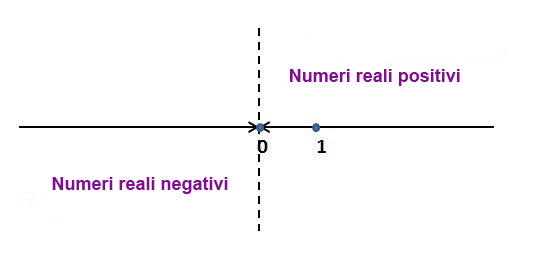
Disegniamo la retta numerica:
I punti della retta rappresentano:
i numeri reali positivi a (a>0) che si trovano a destra dello 0
i numeri reali negativi a (a<0) che si trovano a sinistra dello 0
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Ordinamento dei numeri reali
L'insieme dei numeri reali è un insieme ordinato. Dati due numeri reali arbitrari a e b, valgono le seguenti condizioni:
Un numero a è maggiore di un numero b (ovvero: 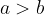 ) quando
) quando  è un numero positivo:
è un numero positivo:
Sulla retta numerica il punto che rappresenta il numero a si trova a destra del punto che rappresenta il numero b.
Rappresentazione grafica:
Un numero a è minore di un numero b (ovvero: 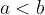 ) quando
) quando  è un numero negativo:
è un numero negativo:
Sulla retta numerica il punto che rappresenta il numero a si trova a sinistra del punto che rappresenta il numero b.
Rappresentazione grafica:
Un numero a è uguale a un numero b (ovvero: 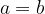 ) quando
) quando  è zero:
è zero:
Sulla retta numerica il punto che rappresenta il numero a coincide esattamente con il punto che rappresenta il numero b.
Rappresentazione grafica:
Possiamo combinare tra loro le condizioni appena viste e definire in modo più generico l'ordinamento dei numeri reali:
Un numero a è maggiore o uguale a un numero b (ovvero: 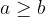 ) quando
) quando  è un numero non negativo:
è un numero non negativo:
Sulla retta numerica il punto che rappresenta il numero a si trova a destra o coincide esattamente con il punto che rappresenta il numero b.
Un numero a è minore o uguale a un numero b (ovvero: 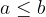 ) quando
) quando  è un numero non positivo:
è un numero non positivo:
Sulla retta numerica il punto che rappresenta il numero a si trova a sinistra o coincide esattamente con il punto che rappresenta il numero b.
Dalle condizioni viste possiamo dedurre la seguente relazione di equivalenza (principio di asimmetria):
Dati due numeri reali arbitrari a e b. Sia a maggiore o uguale a b e sia a minore uguale a b, ne consegue che a è uguale a b:
Qui di seguito vediamo le proprietà che scaturiscono dalle condizioni appena viste:
Proprietà delle disuguaglianze
Dati tre numeri reali arbitrari a, b e c, valgono le seguenti proprietà:
se 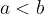 allora
allora 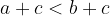
Se si aggiunge uno stesso numero ad entrambi i membri di una disuguaglianza, la disuguaglianza conserva lo stesso verso (monotonia dell'addizione).
Proprietà transitiva della disuguaglianza.
Se si moltiplicano entrambi i membri di una disuguaglianza per uno stesso numero positivo, la disuguaglianza conserva lo stesso verso
Se si moltiplicano entrambi i membri di una disuguaglianza per uno stesso numero negativo, la disuguaglianza cambia di verso





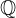
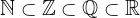
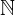 ... insieme dei numeri naturali
... insieme dei numeri naturali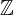 ... insieme dei numeri interi
... insieme dei numeri interi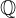 ... insieme dei numeri razionali
... insieme dei numeri razionali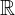 ... insieme dei numeri reali
... insieme dei numeri reali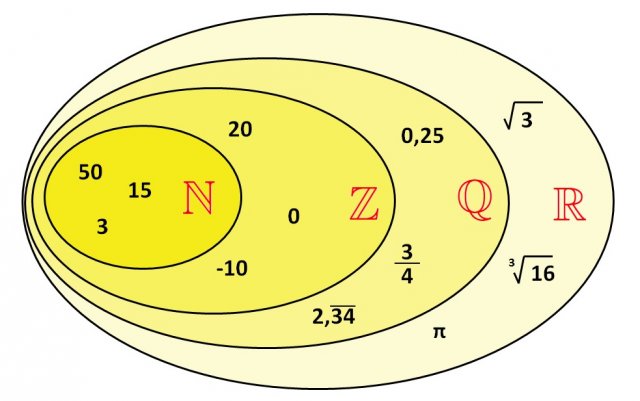
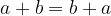
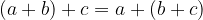
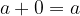
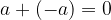
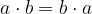
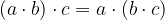
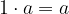
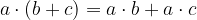
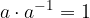
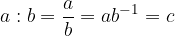
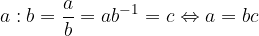
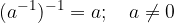
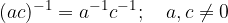
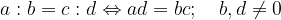
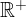 ... insieme dei numeri reali positivi
... insieme dei numeri reali positivi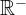 ... insieme dei numeri reali negativi
... insieme dei numeri reali negativi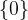 ... insieme contenente il numero zero
... insieme contenente il numero zero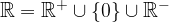
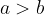 ) quando
) quando  è un numero positivo:
è un numero positivo: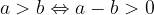

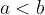 ) quando
) quando 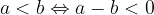

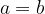 ) quando
) quando 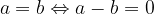

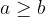 ) quando
) quando  è un numero non negativo:
è un numero non negativo: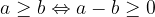
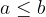 ) quando
) quando 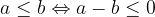
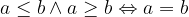
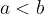 allora
allora 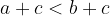
 , allora
, allora 
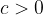 , allora
, allora 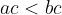
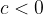 , allora
, allora