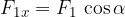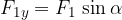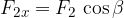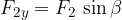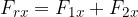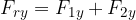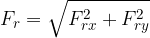Consideriamo un ragazzo che tira una carrucola lungo un pendio, applicando una forza tale da permettere a questa di muoversi. A causa del peso eccessivo della carrucola, il ragazzo chiede l'aiuto di un amico. In questo modo, alla carrucola viene applicata una forza doppia, dal momento che la forza esercitata da entrambi i ragazzi presenta lo stesso punto di applicazione e la stessa direzione.
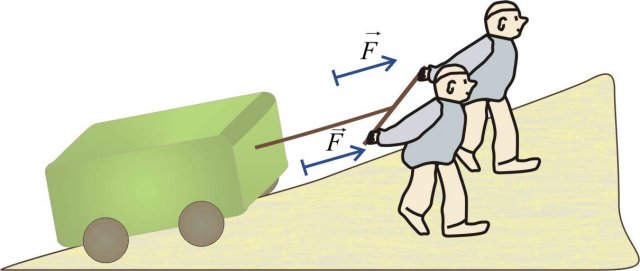
Esempio di due forze uguali applicate ad un corpo
Consideriamo un ragazzo che calcia un pallone. In questo caso, la forza esercitata dalle gambe determina il volo del pallone. Inoltre, pensiamo ad un corpo, dotato di una certa massa, appeso ad una corda elastica. In questo caso, la corda viene allungata dalla forza peso. Oppure, possiamo considerare una pietra che cade sul terreno. Tutti questi fenomeni e molti altri sono il risultato dall'azione di una forza.
Tuttavia, le forze possono agire in modo che il corpo sia in uno stato stazionario (ad esempio: una penna ferma su un tavolo). Questo non implica l'assenza di forze, bensì un bilanciamento delle forze agenti sul corpo. Quindi, l'effetto complessivo su questo risulta essere pari a zero. In questo caso, è possibile affermare che la somma, o risultante, delle forze agenti è pari a zero e quindi il corpo si trova in una condizione stabile, ovvero in equilibrio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il concetto di forza viene introdotto in diversi argomenti:
Gravità, la quale viene espressa dalla legge di gravitazione di Newton e dalle leggi di Keplero, che descrivono i movimenti dei corpi celesti.
In questa sezione ci focalizzeremo sui principali concetti relativi alle forze: mostreremo che una forza è un vettore e consolideremo alcune conoscenze matematiche su questi ultimi.
Che cosa è una forza?
Una forza è una grandezza fisica vettoriale. Generalmente una forza viene indicata con F, e la relativa unità di misura nel SI (Sistema Internazionale) è il newton (N).
In fisica l'esistenza di una forza si manifesta tramite l'effetto che esercita sul corpo su cui agisce. L'azione di una forza può determinare:
una variazione della velocità del corpo
una variazione della direzione del moto del corpo
una deformazione del corpo
L'azione di una forza su un secondo corpo può avvenire mediante:
contatto diretto con il corpo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
effetto a distanza. Consideriamo la forza gravitazionale 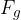 . Questa agisce a distanza ed è il risultato di una forza attrattiva tra la terra ed un dato corpo.
. Questa agisce a distanza ed è il risultato di una forza attrattiva tra la terra ed un dato corpo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La forza come vettore
Come tutti i vettori, il vettore forza è caratterizzato da (vedi figura 1):
un punto di applicazione, in cui la forza viene applicata al corpo, ed una direzione;
un modulo, il quale è rappresentato graficamente dalla lunghezza di un segmento orientato, proporzionale alla intensità della forza;
un verso, indicato da una freccia.
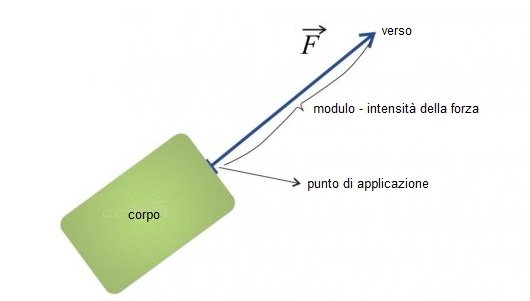
Figura 1: Rappresentazione grafica di una forza F
L'azione di una forza su un corpo può avere lo stesso effetto nonostante agisca su punti di applicazione differenti. Consideriamo il seguente esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Data la natura vettoriale delle forze, è fondamentale approfondire ulteriormente le proprietà matematiche di base dei vettori. In particolare, tratteremo:
Che cosa è uno spostamento parallelo di un vettore e perchè viene usato nei grafici e nelle operazioni tra vettori.
Come si sommano le forze (vettori).
Che cosa è una forza opposta e come viene usata nel caso di differenze tra vettori.
Come scomporre una forza nelle sue componenti.
Cosa si intende per equilibrio delle forze.
il vettore forza è definito da:
Il punto di applicazione è il punto attraverso cui una forza è applicata su un secondo corpo.
L'azione di una forza su un corpo si manifesta con una variazione della velocità o con una deformazione del corpo.
Una forza può agire su un corpo tramite:
Somma e sottrazione di forze
Quando sommiamo (o sottraiamo) delle forze otteniamo il vettore somma delle forze, denominato anche come risultante.
Per il calcolo del vettore somma (o risultante) delle forze è possibile utilizzare un approccio grafico o vettoriale.
Spostamento parallelo di forze
Il vettore somma di due forze può essere calcolato effettuando il cosidetto spostamento parallelo. Questa regola afferma che la lunghezza, la direzione ed il verso di un vettore rimangono inalterate qualora questo subisca uno spostamento parallalelo al piano o allo spazio. Si tratta di uno strumento matematico utilizzato per facilitare la somma di vettori, a seguito della quale questi vengono considerati nuovamente nella loro posizione iniziale.
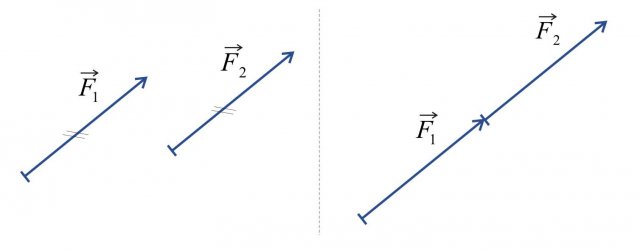
Figura 3: i due vettori nell'immagine a sinistra (o solo uno dei due) possono essere spostati in modo che questi siano disposti lungo lo stesso asse (come mostrato a destra) .
la loro uguaglianza viene evidenziata da due trattini paralleli (Figura 3, sinistra). In questo caso:
Forze opposte
Due forze si dicono opposte se possiedono lo stesso modulo e direzione opposta. Ciò implica che la loro risultante è nulla e, di conseguenza, non ha alcuna influenza sul sistema fisico in questione, come accennato all'inizio del capitolo.

Figura 4: forze opposte con lo stesso punto di applicazione.
Le forze mostrate in Figura 4 hanno lo stesso modulo ma sono dirette in verso opposto. Quindi la loro somma è pari a zero:
La forza negativa è ottenuta mantenendone intalterata la dimensione e invertendone la direzione. Di conseguenza, la somma di due forze opposte è pari a 0.
Nel capitolo sul moto uniformemente accelerato sarà mostrato che se un corpo è sottoposto all'azione di due forze opposte si trova in uno stato stazionario.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma di forze
La somma di due o più forze, chiamate componenti, dà origine ad una nuova forza, chiamata risultante. Questa, determina sul corpo, lo stesso effetto che determinerebbero tutte le componenti insieme.
Per il calcolo della risultante, è utile utilizzare un disegno, tramite il quale il problema risulterà notevolmente semplificato.
La somma di due o più forze può essere effettuata utilizzando i seguenti metodi grafici:
regola del parallelogramma;
Regola del parallelogramma
Consideriamo due forze caratterizzate dallo stesso punto di applicazione, come mostrato in Figura 5:
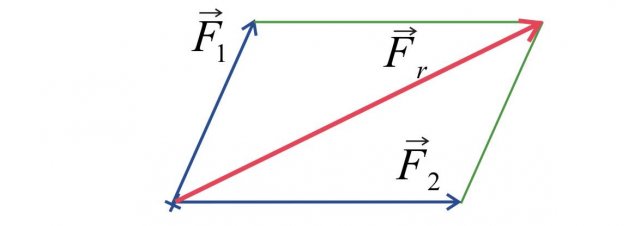
Figura 5: Esempio della regola del parallelogramma.
La somma di due forze, tramite la regola del parallelogramma, si basa sulla seguente procedura:
Si effettua uno spostamento parallelo delle forze che si vogliono sommare in modo che abbiano lo stesso punto di applicazione (frecce blu).
Si disegna un vettore parallelo alla prima forza e lo si posiziona alla fine della seconda forza (segmento verde).
Analogamente, si disegna un vettore parallelo alla seconda forza e lo si posiziona alla fine della prima (segmento verde).
I vettori disegnati costituiscono un parallelogramma. La risultante è determinata dalla diagonale maggiore del parallelogramma (freccia rossa).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Poligono delle forze
Consideriamo un sistema fisico caratterizzato da più forze. Queste possono essere sommate nel seguente modo:
Si disegni la prima forza (l'ordine scelto è ininfluente);
Si posizioni il punto di applicazione della seconda forza nel punto finale della prima forza (anche in questo caso l'ordine con cui si sceglie la seconda forza non conta);
Si prenda un'arbitraria terza forza e la si posizioni con uno spostamento parallelo al termine della seconda forza.
Si ripeta questa opeazione fino al termine delle forze.
La risultante, pari alla somma di tutte le forze, è ottenuta congiungendo il punto di applicazione della prima forza con il punto finale dell'ultima forza.
La risultante può essere nuovamente spostata in modo parallelo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La somma di due o più forze può essere effettutata graficamente utilizzando la regola del parallelogramma o tramite il poligono delle forze.
Regola del parallelogramma
Tramite questa regola è possibile sommare simultaneamente solo due vettori (dopo aver fatto coincidere il punto di applicazione). Si disegna un vettore parallelo al primo e lo si posiziona al termine del secondo vettore. Si procede analogamente per l'altro vettore. La risultante è determinata dalla diagonale maggione del parallelogramma formato.
Supponiamo di avere tutte le forze con lo stesso punto di applicazione rispetto al sistema di coordinate. Si muove la seconda forza in modo che il punto di applicazione di questa termini sul punto finale della prima, e cosi via. La risultante è determinata dalla congiungente tra il punto di applicazione della prima forza e il punto finale dell'ultima.
Differenza di due vettori
Spostiamo (in modo parallelo) la forza 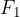 nel punto in cui vogliamo rappresentare l'operazione.
nel punto in cui vogliamo rappresentare l'operazione.
Facendo precedere la forza 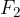 dal segno meno (-
dal segno meno (- 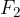 ), questa diventa caratterizzata da verso opposto.
), questa diventa caratterizzata da verso opposto.
Congiungendo l'inizio del primo vettore e la fine del secondo vettore, otteniamo il risultato:
Operazione di sottrazione tra due vettori:
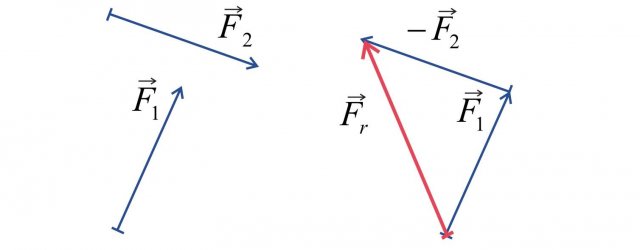
Figura 8: differenza di due vettori.
Addizione e sottrazione di forze parallele
Le forze parallele si sommano insieme analogamente al caso del poligono delle forze. Infatti, queste si spostano, parallelamente, in modo che il loro punto di partenza sia sempre coincidente con il punto terminale della forza precedente (si noti che una forza negativa cambia verso). Dunque, la risultante delle forze è ottenuta congiungendo l'inizio della prima forza e la fine dell'ultima.

Figura 9: addizione e sottrazione di forze parallele.
Scomposizione della forza nelle sue componenti
Il processo di scomposizione di una forza F nelle sue componenti rappresenta l'operazione inversa rispetto alla regola del parallelogramma, precedentemente utilizzata per il calcolo delle risultante di più forze. Se consideriamo la scomposizione di una forza in due componenti (nel piano), è necessario definire le direzioni di queste ultime (nel medesimo piano).
Prendiamo in esame il seguente esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equilibrio di forze
Le forze agenti su un corpo risultano essere in equilibrio quando la relativa risultante è pari a zero. In questo caso il corpo non subisce variazioni di velocità, ovvero resta in quiete oppure si muove di moto rettilineo uniforme. Ogni qualvolta osserviamo in natura un corpo fermo, possiamo dedurre che tutte le forze agenti su quel corpo sono in equilibrio, ossia che la loro risultante è pari a zero.
Come abbiamo precedentemente discusso, due forze opposte ed eguali in modulo possiedono risultante nulla. Quindi, un corpo soggetto ad una coppia di forze di questo tipo risulta essere in quiete.
Inoltre, consideriamo la condizione di equilibrio tramite il poligono delle forze. In questo caso, le forze sono in equilibrio se il punto finale dell'ultima forza del poligono ed il punto iniziale della prima forza coincidono (vedi Figura 11).
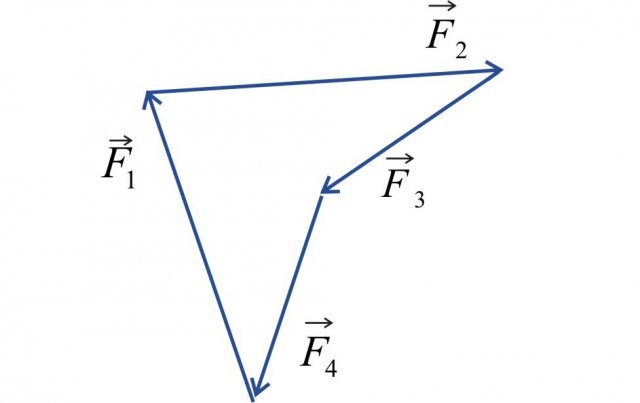
Figura 11: la condizione di equilibrio si manifesta con la chiusura del poligono delle forze, la cui risultante è pari a zero.
Le forze, agenti su un dato corpo, sono in equilibrio, se la loro risultante è nulla. In questo caso il corpo è in quiete oppure si muove di moto rettilineo uniforme.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma di vettori utilizzando le componenti x ed y
la componente lungo la direzione dell'asse x, 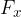 ;
;
la componente lungo la direzione dell'asse y, 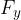 ;
;
Per comodità, prendiamo ad esempio due vettori; analogamente, è possibile estendere la procedura al caso di più vettori.
I vettori (frecce nella Figura 13) possono essere sommati insieme nel sistema di coordinate Cartesiane in modo che siano prima scomposti nelle componenti lungo la direzione dell'asse x e y (linee tratteggiate in Figura 13).
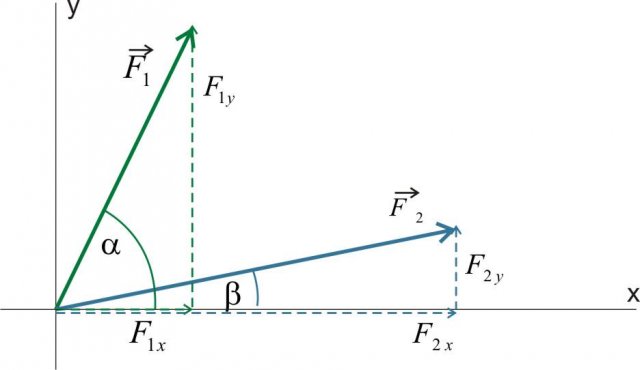
Figura 13: disponiamo i vettori nel sistema di riferimento Cartesiano.
La componente x del vettore risultante è costituita dalla somma delle componenti x di ciascun vettore, mentre la componente y del vettore risultante è costituita dalla somma delle componenti y di ciascun vettore:
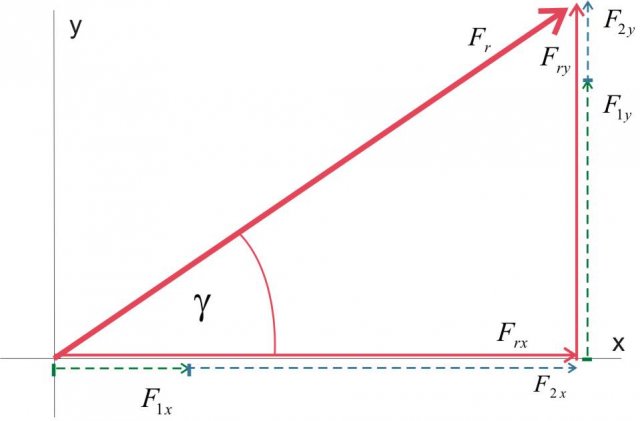
Figura 14: vettore risultante.
Le componenti del vettore risultante possono essere scritte come la somma delle relative componenti dei vettori da sommare:
Il vettore assoluto del vettore risultante è ottenuto tramite il teorema di Pitagora:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





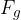 . Questa agisce a distanza ed è il risultato di una forza attrattiva tra la terra ed un dato corpo.
. Questa agisce a distanza ed è il risultato di una forza attrattiva tra la terra ed un dato corpo.

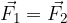

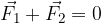
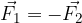

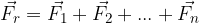
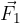 ed
ed 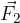 può essere interpretata come la somma tra la forza
può essere interpretata come la somma tra la forza 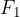 nel punto in cui vogliamo rappresentare l'operazione.
nel punto in cui vogliamo rappresentare l'operazione.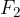 dal segno meno (-
dal segno meno (- 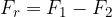


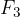 . Collegando l'inizio di
. Collegando l'inizio di 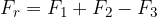

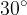 ,
, 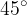 e
e 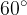 . In questo caso è possibile usare conoscenze geometriche di base, come quelle relative a
. In questo caso è possibile usare conoscenze geometriche di base, come quelle relative a 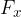 ;
;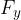 ;
;