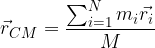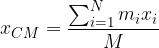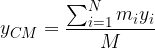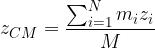Fino ad ora abbiamo considerato sempre punti materiali. Ora ci chiediamo cosa accade se i corpi sono estesi. Pensiamo ad esempio al volante di un'auto. Su di esso è applicato una forza F che agisce nella direzione di rotazione del volante (vedere Figura 1). La direzione della forza è quindi tangente alla circonferenza, che è rappresentata dal volante. Il volante ruota intorno al'asse centrale, chiamato anche asse di rotazione o fulcro. La distanza tra la forza e il fulcro è detta braccio della forza b.
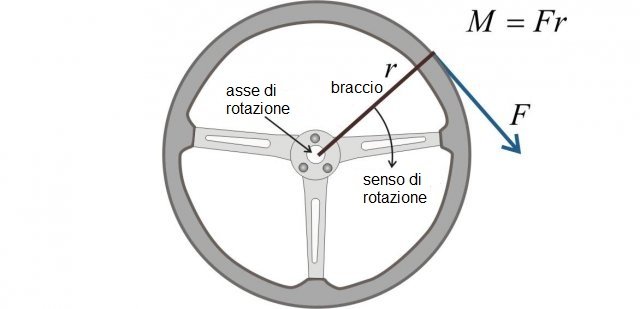
Figura 1: La forza sul volante di un'auto.
Il prodotto della forza esercitata sul volante e il braccio, che in questo caso è uguale al raggio r della circonferenza, è chiamato momento della forza:
L'equazione scritta si applica solo se la forza e il braccio sono perpendicolari.
Il risultato di un momento è la rotazione. Esso infatti in termini più tecnici descrive l'attitudine di una forza a imprimere la rotazione ad un oggetto attorno al fulcro.
Il momento sarà maggiore, tanto maggiore sarà la forza e/o il braccio.
Per dare un segno positivo o negativo, dobbiamo scegliere un senso di rotazione. Convenzionalmente viene scelto il verso antiorario come positivo.
L'unità del momento è Nm (Newton per metro).
Il momento è il prodotto tra la forza e il braccio se la forza e il braccio sono ortogonali:
Può essere positivo o negativo a seconda della rotazione, solitamente positivo se antiorario.
In questo documento impareremo:
come calcolare il momento anche se la forza e la leva non sono ortogonali;
come il momento agisce sul corpo;
cosa accade quando ci sono più forze;
quando i momenti sono in equilibrio;
Calcolo del momento
Il momento è un vettore, quindi ha un modulo, una direzione e un verso. Il momento è dato dalla seguente equazione:
Dalle proprietà del prodotto vettoriali sappiamo che:
il modulo è dato dall'equazione
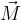 è diretto lungo la retta ortogonale al piano contenente i due vettori.
è diretto lungo la retta ortogonale al piano contenente i due vettori.
il verso viene ricavato dalla regola della mano destra. Si mette l'indice lungo il primo vettore e il medio lungo secondo, il pollice ci darà il verso del vettore risultante, se entrante nel piano dei vettori è negativo mentre se uscente positivo. Aiutiamoci con l'immagine:
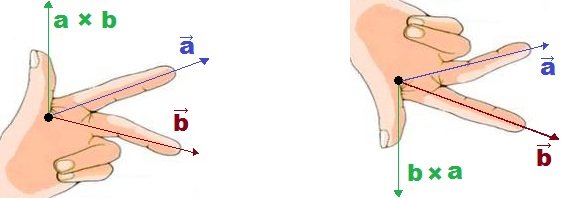
Figura 5: Direzione e verso di un prodotto vettoriale
Il verso ci indica in quale verso ruota il corpo, sui è applicata la forza.
Il modulo nel caso 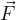 e
e 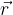 siano ortogonali è proprio:
siano ortogonali è proprio:
Per comodità di scrittura molte volte invece di 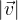 si usa semplicemente
si usa semplicemente 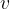 senza la freccetta.
senza la freccetta.
Il momento è un vettore dato dall'equazione:
direzione:lungo la retta ortogonale al piano contenente i due vettori.
verso: il verso viene ricavato dalla regola della mano destra.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma di momenti
Su un corpo possono agire più momenti. La risultante dei momenti si ottiene sommando tra loro i singoli momenti, cioè la somma di n momenti è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'equilibrio di forze e momenti
Nei capitoli precedenti abbiamo appreso che un corpo è in equilibrio se la somma delle forze agenti sul corpo è nulla. In questo caso, il corpo è fermo o si muove in modo uniforme e rettilineo.
E se la somma delle forze è zero, la somma dei momenti come è? Sulla somma dei momenti non possiamo dire nulla a partire dalla somma delle forze (approfondiremo l'argomento nel capitolo sul momento angolare).
In questo capitolo ci limiteremo al caso in cui la somma di tutte le forze e la somma di tutti i momenti sono uguali a zero. Il corpo si dice che è quindi in equilibrio meccanico. Ciò significa che non accelera e non ruota.
Se il corpo è in equilibrio meccanico non accelera e non ruota. La condizione per l'equilibrio meccanico è che la somma di tutte le forze che agiscono sul corpo, e la somma di tutti i momenti siano:
Queste due equazioni vettoriali sono indipendenti, cioè non possiamo ricavare l'una dall'altra.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il centro di massa
Definiamo adesso il centro di massa, che ci semplificherà sia in termini di calcoli che di intuizione del problema per la fisica dei corpi estesi e anche dei sistemi a più particelle.
Immaginiamo di avere N particelle e ciascuna di queste abbia massa 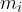 posizione nello spazio
posizione nello spazio 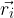 rispetto a un arbitrario sistema di coordinate. Definiamo centro di massa il punto di posizione:
rispetto a un arbitrario sistema di coordinate. Definiamo centro di massa il punto di posizione:
Indicando con M la massa totale del sistema:
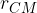 diventa:
diventa:
Questa equazione può essere scomposta nelle tre componenti:
Per i corpi estesi l'argomento è matematicamente più complicato, perciò prendiamo solo alcuni casi notevoli, quali:
per un rettangolo o un quadrato, il centro di massa si trova al centro - cioè, all'intersezione delle diagonali.
per una sfera o una circonferenza il CM è nel centro della sfera o della circonferenza.
per un cilindro il CM si trova sull'asse di rotazione a meta dell'altezza.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





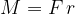
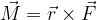
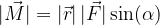
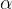 è l'angolo tra i vettori
è l'angolo tra i vettori 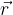 e
e 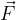 .
.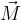 è diretto lungo la retta ortogonale al piano contenente i due vettori.
è diretto lungo la retta ortogonale al piano contenente i due vettori.
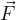 e
e 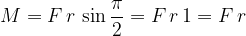
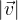 si usa semplicemente
si usa semplicemente 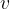 senza la freccetta.
senza la freccetta.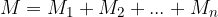
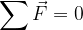
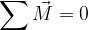
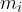 posizione nello spazio
posizione nello spazio 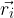 rispetto a un arbitrario sistema di coordinate. Definiamo centro di massa il punto di posizione:
rispetto a un arbitrario sistema di coordinate. Definiamo centro di massa il punto di posizione: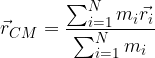
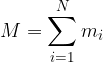
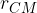 diventa:
diventa: