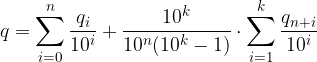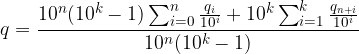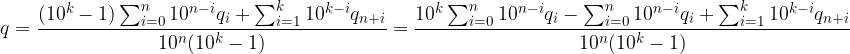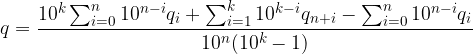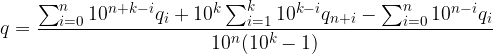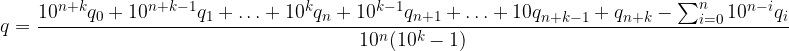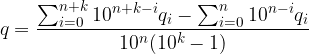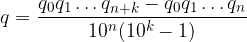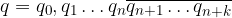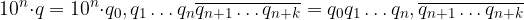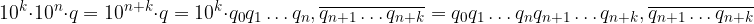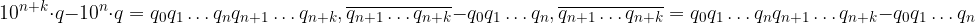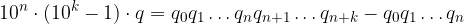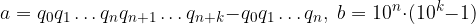Nel capitolo Numeri Decimali abbiamo introdotto una scrittura equivalente alle frazioni, dei metodi per convertire l'una nelle altre e alcune operazioni senza fornire una giustificazione precisa. In questo capitolo - avendo la nozione di Successione e di Serie - riprendiamo le espansioni decimali e qualche operazione. Dedichiamo gli ultimi capitoli alle espansioni in una base qualunque.
Definizione
Il primo termine della serie si chiama Parte Intera:
Il resto della serie si chiama Parte Frazionaria:
I termini di tale successione sono le cifre dell'espansione decimale e quelle della parte frazionaria sono comprese tra 0 e 9:
Al posto del simbolo di serie useremo la notazione abituale con la virgola o il punto dopo il primo termine:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Osservazione
È una buona definizione? Ovvero - data la successione delle cifre dell'espansione decimale 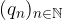 - la serie converge?
- la serie converge?
La risposta è affermativa.
Consideriamo la parte frazionaria:
Ogni termine generico è maggiorato dalla frazione 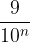 :
:
Riconduciamo la serie di termine generale 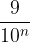 ad una serie geometrica di ragione
ad una serie geometrica di ragione 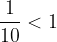 che è convergente:
che è convergente:
L'espansione decimale è un numero reale perché dato dalla somma della sua parte intera (un numero intero) con la sua parte frazionaria (un numero reale):
Espansioni Decimali Generate da Razionali
Nel capitolo Numeri Decimali abbiamo introdotto l'algoritmo esteso di Euclide che permette di convertire una frazione nella sua espansione decimale:
Formalizziamo tale algoritmo.
Dividere il numeratore per il denominatore con l'usuale algoritmo. Il quoziente è la parte intera.
Moltiplicare per 10 il resto ottenuto:
Spostarsi di una cifra decimale a destra. Nel caso in cui si calcoli la prima cifra decimale si frappone un punto (virgola) tra esso e la parte intera:
Dividere il nuovo resto per il denominatore con l' usuale algoritmo. Il quoziente è la cifra decimale:
Una condizione di terminazione per l'algoritmo naturale è quando si giunge ad un resto nullo (numero decimale finito). Tuttavia dato che esistono espansioni decimali periodiche segue che:
L'algoritmo precedente potrebbe non terminare!
Una soluzione a questo problema è di indebolire la condizione di terminazione:
L'algoritmo termina se si ripresenta un resto già apparso prima.
In questo modo comprendiamo anche le espansioni decimali periodiche.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un'interpretazione dell' algoritmo esteso di Euclide è quella di approssimare un numero razionale tramite suddivisioni di potenze di 10.
Cominciamo con l'approfondire le espansioni decimali più semplici: espansioni decimali finite o limitate.
Espansioni Limitate
è Limitata o Finita se la parte frazionaria è definitivamente nulla:
Per non appesantire la scrittura omettiamo tali cifre:
Un'espansione decimale è limitata se nell'algoritmo appare un resto nullo:
Dimostriamolo per induzione.
Supponiamo di essere all'n+1-esimo passo dell'algoritmo:
Supposto che il resto n-esimo sia nulla deduciamo che anche il resto successivo è nullo:
Torniamo all'n+1-esimo passo dell'algoritmo:
Sostituiamo i resti nulli:
Per la legge di annullamento di un prodotto - dato che b non è nullo - il quoziente n+1-esimo è nullo:
Vedremo più avanti una condizione sul denominatore di una frazione affinché la sua espansione decimale sia finita.
Espansioni Illimitate Periodiche
è Illimitata Periodica se la parte frazionaria è definitivamente periodica:
Per non appesantire la scrittura disegniamo una linea sopra le cifre che si ripetono e le omettiamo dalla II volta in poi :
Il Periodo è l'insieme delle cifre che si ripetono:
k è Lunghezza del periodo.
L'Anti-periodo è l'insieme delle cifre decimali che non si ripetono:
n è la Lunghezza dell'anti-periodo.
Espansioni Illimitate Periodiche Semplici
Un' Espansione Illimitata Periodica è Semplice se l'anti-periodo è lungo 0 (non vi sono cifre anti-periodiche).
Tale espansione sarà della forma:
La prima condizione naturale che possiamo immaginare affinché un numero decimale sia periodico semplice è che le cifre dopo la virgola si ripropongano spostandosi di k posizioni:
In realtà una condizione sufficiente è che i resti si ripetano ciclicamente dopo k passi:
Un'espansione decimale è periodica semplice se nell'algoritmo riappaiono ciclicamente i resti a partire dal primo:
L'ipotesi è che per ogni indice n, il resto non cambia dopo k cifre:
Applichiamo a tali resti l'algoritmo di Euclide:
Sottraiamo la I equazione alla II e raccogliamo dove possibile:
Per ipotesi resti che differiscono di k cifre sono uguali, quindi la loro differenza è nulla:
Per la legge di annullamento di un prodotto - dato che b non è nullo - la differenza è nulla, ovvero minuendo e sottraendo sono uguali:
Vedremo più avanti una condizione sul denominatore di una frazione affinché la sua espansione decimale sia periodica semplice.
Espansioni Illimitate Periodiche Miste
Un'espansione Illimitata Periodica è Mista se l'anti-periodo ha lunghezza maggiore di 0 (vi è almeno una cifra anti-periodica).
Tale espansione sarà della forma:
Tale espansione generalizza quella limitata in quanto si ha per k = 0 e quella periodica semplice nel caso n = 0.
La dimostrazione che le cifre si ripetono solo se i resti sono ciclici è del tutto analoga ai decimali periodici semplici.
Vedremo più avanti una condizione sul denominatore di una frazione affinché la sua espansione decimale sia periodica semplice.
Operazioni con le Espansioni Decimali
In questo capitolo svolgeremo alcune operazioni con le espansioni decimali per studiarne gli effetti sulla loro scrittura.
Moltiplicazione per potenza di 10
Consideriamo un'espansione decimale:
Moltiplichiamola per una potenza di 10:
Applichiamo la proprietà distributiva:
Ricordiamo la scrittura polinomiale di un numero intero con n+1 cifre in base 10:
Notiamo che la prima parte dell'espansione decimale è la scrittura polinomiale di un numero intero con k+1 cifre, mentre la seconda è la sua parte frazionaria:
La virgola si è spostata di k posti a destra.
Moltiplicare k volte un'espansione decimale per 10 sposta la virgola a destra di k posti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione per potenza di 10
Per i numeri razionali la divisione tra due numeri è il prodotto tra il primo ed il reciproco del secondo, quindi dividere un'espansione decimale per una potenza positiva di 10 equivale a moltiplicare tale espansione decimale per una potenza negativa di 10.
Consideriamo un'espansione decimale:
Moltiplichiamola per una potenza negativa di 10:
Applichiamo la proprietà distributiva:
Tale scrittura non sembra essere un'espansione decimale in quanto se proviamo a scriverla come serie numerica non partiamo dall'indice n = 0, ma dall'indice n = k:
Tuttavia l'espansione decimale non cambia se aggiungiamo un numero finito di addendi nulli:
In questo modo, però, riusciamo a scrivere la serie numerica come espansione decimale:
La nuova successione di cifre è nulla per i primi k termini e coincide con quella vecchia dal k+1-esimo:
Concludiamo scrivendo il risultato della divisione:
La virgola si è spostata di k posti a sinistra.
Dividere k volte un'espansione decimale per 10 sposta la virgola a sinistra di k posti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma e Sottrazione
Non possiamo sommare o sottrarre due espansioni decimali come numeri decimali finiti partendo dalla cifra più a destra in quanto generalmente vi sono infinite cifre a destra della virgola.
Procediamo, invece, come per i numeri decimali periodici, dove ripetevamo più volte la medesima operazione approssimando sempre meglio (coinvolgendo sempre più cifre) il risultato.
Consideriamo due espansioni decimali:
Per determinare quali sono le cifre incerte dobbiamo stimare l'errore commesso, ovvero il modulo della differenza tra la somma e quella approssimata.
Chiamiamo x la loro somma e 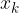 la somma approssimata con k cifre decimali:
la somma approssimata con k cifre decimali:
Il modulo della differenza è dell'ordine di 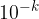 :
:
Applichiamo la disuguaglianza triangolare:
Possiamo considerare le serie numeriche dentro i moduli come parti frazionarie di un'opportuna espansione decimale:
Quando abbiamo controllato la bontà della definizione delle espansioni decimali abbiamo visto che la parte frazionaria è sempre minore o uguale a 1:
Nella nostro caso ci permette di maggiorare l'errore:
La somma tra due espansioni decimali approssimate è incerta sulla cifra più a destra.
Consideriamo meglio la frazione 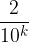 .
.
Essa ci dice non solo la cifra incerta (ordine di grandezza dell'errore), ma anche il suo allontanamento massimo: 1 cifra.
Dato che siamo in base 10 - le cifre "critiche" sono 0 e 9 - in quanto influenzano la cifra vicina - quindi per calcolare esattamente alcune cifre di una somma è necessario capire se la cifra incerta è 0 o 9 e come influenza quelle vicine.
La somma approssimata tra due espansioni decimali coincide con quella esatta se la cifra incerta non è 0 né 9.
Vediamo un esempio in cui la cifra incerta non è 0 né 9.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo un esempio in cui la cifra incerta è 0 o 9.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Numeri Razionali Generanti Espansioni Decimali
Nel capitolo Numeri Decimali abbiamo fornito alcuni modi eqivalenti per convertire un'espansione decimale periodica in una frazione che lo genera:
Dettagliamo meglio questi metodi e dimostriamo che sono equivalenti.
Conversione di Decimali Finiti
Ci sono 3 modi equivalenti per convertire un decimale finito in frazione:
Metodo Elementare. Consideriamo un espansione decimale finita:
Le cifre sono definitivamente nulle e la serie si riduce ad una sommatoria:
Otteniamo la frazione generatrice sommando tutte queste frazioni:
Metodo Posizionale. Partiamo dall'ultima uguaglianza del punto precedente:
Scriviamo la sommatoria come un'unica frazione:
La sommatoria è un numero scritto in base 10 con le cifre dell'espansione decimale:
Metodo Operativo. Consideriamo un espansione decimale finita:
Moltiplichiamo l'espansione per 10 alla numero di cifre decimali:
Il II membro è un numero intero scritto in base 10. Diamo un nome al coefficiente di q ed al termine noto:
Sostituiamo. L'uguaglianza diventa:
Concludiamo per la definizione di frazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Conversione di Decimali Periodici Semplici
Ci sono 3 modi equivalenti per convertire un decimale periodico semplice in frazione:
Metodo Elementare. Consideriamo un espansione decimale periodica semplice:
Raccogliamo parzialmente le frazioni comuni:
Raccogliamo la serie comune:
La serie presente è geometrica di ragione 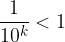 per k > 1. Calcoliamone la somma:
per k > 1. Calcoliamone la somma:
Otteniamo la frazione generatrice svolgendo tutti i calcoli:
Metodo Posizionale. Partiamo dall'ultima uguaglianza del punto precedente:
Scriviamo una sola frazione:
Inglobiamo il primo addendo nella sommatoria:
La sommatoria è un numero scritto in base 10 con le cifre dell'espansione decimale:
Metodo Operativo. Consideriamo un espansione decimale periodica semplice:
Moltiplichiamo l'espansione per 10 alla numero di cifre periodiche:
Sottraiamo a tale numero quello iniziale:
Raccogliamo q al I membro:
Il II membro è un numero intero perché differenza di interi. Diamo un nome al coefficiente di q ed alla differenza:
Sostituiamo. L'uguaglianza diventa:
Concludiamo per la definizione di frazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Conversione di Decimali Periodici Misti
Ci sono 3 modi equivalenti per convertire un decimale periodico misto in frazione:
Metodo Elementare. Consideriamo un espansione decimale periodica mista:
Raccogliamo parzialmente le frazioni comuni con le cifre periodiche:
Raccogliamo la serie comune:
La serie presente è geometrica di ragione 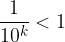 per k > 1. Calcoliamone la somma:
per k > 1. Calcoliamone la somma:
Otteniamo la frazione generatrice svolgendo tutti i calcoli:
Metodo Posizionale. Partiamo dall'ultima uguaglianza del punto precedente:
Raccogliamo 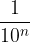 dalla seconda sommatoria:
dalla seconda sommatoria:
Scriviamo una sola frazione:
Riordiniamo le sommatorie:
Scriviamo per esteso le prime due sommatorie:
Sintetizziamo la prime n + k somme:
Le due sommatorie sono numeri scritti in base 10 con le cifre dell'espansione decimale:
Metodo Operativo. Consideriamo un espansione decimale periodica mista:
Moltiplichiamo l'espansione per 10 al numero di cifre non periodiche:
Ci siamo ricondotti al caso delle espansioni decimali periodiche semplici. Moltiplichiamo l'ultima espansione per 10 al numero di cifre periodiche:
Sottraiamo a tale numero il prodotto precedente:
Fattorizziamo il I membro:
Il II membro è un numero intero perché differenza di interi. Diamo un nome al coefficiente di q ed alla differenza:
Sostituiamo. L'uguaglianza diventa:
Concludiamo per la definizione di frazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Conclusione
Per una frazione l'algoritmo di Euclide termina in quanto le cifre a disposizione nella base decimale sono 0, ... , 9 e continuando a dividere sempre con il medesimo numero (il denominatore) prima o poi riapparirà un resto già precedentemente calcolato.
Con questo abbiamo dimostrato che ogni numero razionale genera un'unica espansione decimale periodica.
Tuttavia in seguito siamo partiti da un'espansione decimale periodica e siamo arrivati alla sua frazione generatrice operando unicamente sulle cifre che la compongono.
Con questo abbiamo dimostrato che ogni espansione decimale periodica è generato da un unico numero razionale.
In conclusione le frazioni e le espansioni decimali periodiche sono descrizioni equivalenti dei numeri razionali.


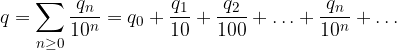
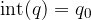
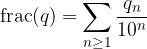
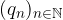 è una successione di
è una successione di 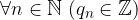
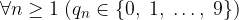

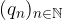 - la
- la 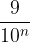 :
: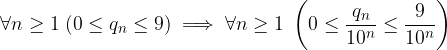
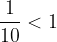 che è convergente:
che è convergente: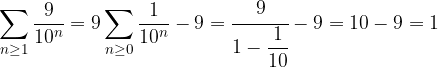
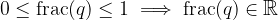
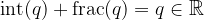
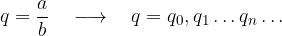
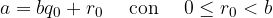
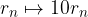

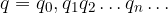
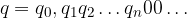
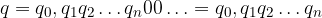
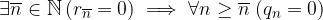
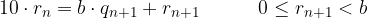
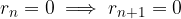
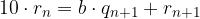
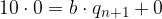
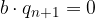
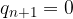
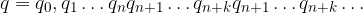
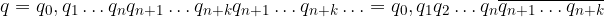
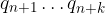
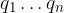
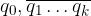
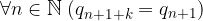
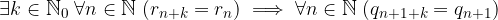
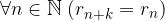
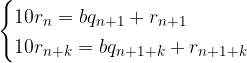
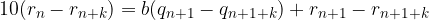
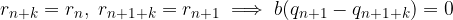
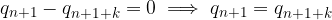
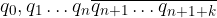
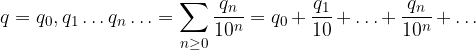
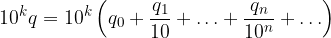
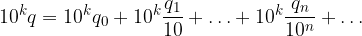
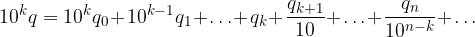
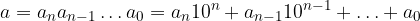
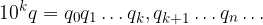
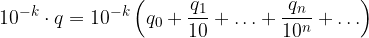
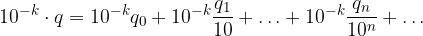
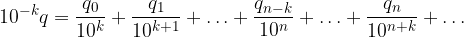
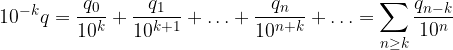
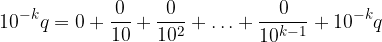
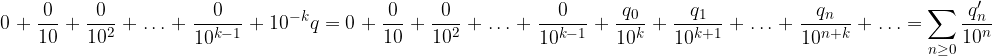
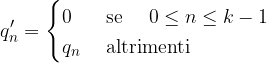
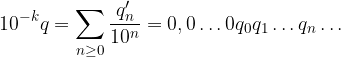
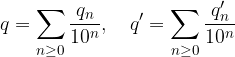
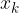 la somma approssimata con k cifre decimali:
la somma approssimata con k cifre decimali: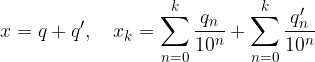
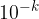 :
: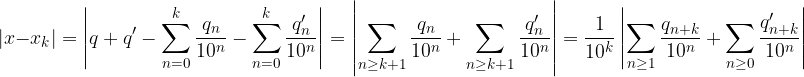
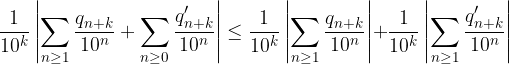
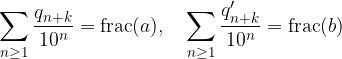
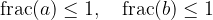
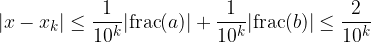
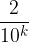 .
.
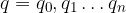
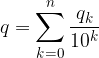
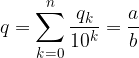
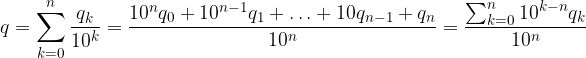
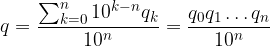
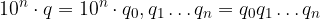
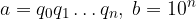
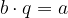
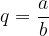
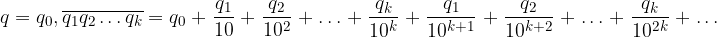
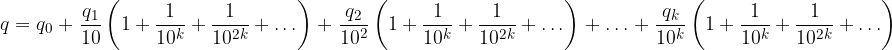
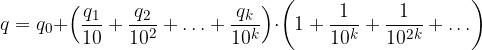
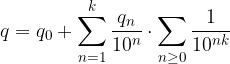
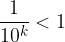 per k > 1. Calcoliamone la somma:
per k > 1. Calcoliamone la somma: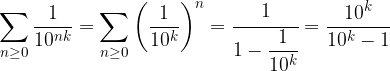
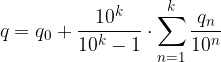
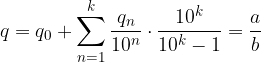
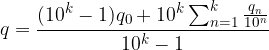
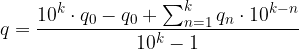
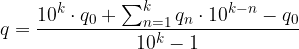
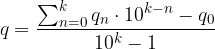
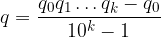
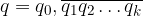
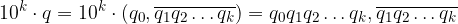
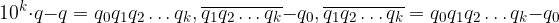
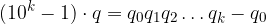
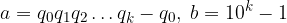
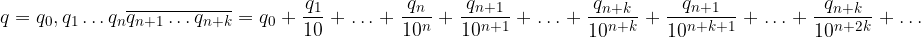
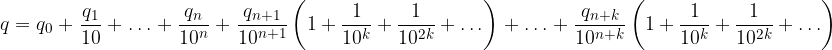
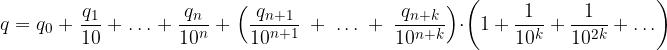
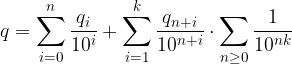
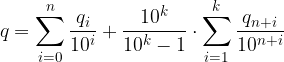
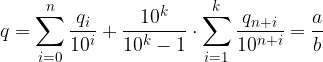
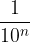 dalla seconda sommatoria:
dalla seconda sommatoria: