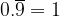In questa sezione vedremo da vicino come le frazioni si possano scrivere come numeri decimali e viceversa.
Una frazione decimale è una frazione che ha come denominatore una potenza di 10 (1, 10, 100, 1000, ...). Questa scelta è dettata dal fatto che la base in cui scrivono solitamente i numeri è quella decimale e perché risulta particolarmente semplice moltiplicare tali frazioni per potenze di 10.
Un numero decimale è un numero intero seguito da una virgola (o un punto) e da altre cifre. Le cifre dopo la virgola (punto) si chiamano cifre decimali ed le prime tre posizioni dopo la virgola hanno dei nomi propri, a seconda della loro posizione prendono nomi diversi:
Il primo posto dopo la virgola (punto) è occupato dai decimi
Il secondo posto dopo la virgola (punto) è occupato dai centesimi
Il terzo posto dopo la virgola (punto) è occupato dai millesimi
Scriviamo alcune corrispondenze tra frazioni decimali e numeri decimali
Se una frazione ha denominatore prodotti di potenze di 2 o 5 allora esso si può scrivere come frazione decimale e convertire infine a numero decimale. Vediamo alcuni esempi.
Applicando il procedimento inverso è possibile passare da numeri decimali a frazioni eventualmente riducibili.
Abbiamo trattato nei paragrafi precedenti con numeri decimali finiti (le cifre decimali erano in numero finito) e frazioni i cui denominatori sono prodotti di potenze di 2 o 5 e ne abbiamo scoperto una corrispondenza.
Tuttavia esistono sia numeri decimali che non hanno un numero finito di cifre decimali sia frazioni i cui denominatori non sono (solo) prodotti di potenze di 2 o 5.
Vedremo che vi sarà una corrispondenza tra tali frazioni e particolari decimali illimitati: i numeri decimali periodici.
Un numero decimale periodico è un numero decimale in cui da una certa cifra decimale iniziano a ripetersi un numero finito di cifre nel medesimo ordine.
In un numero decimale periodico si chiama periodo l' insieme delle cifre decimali che si ripetono, anti-periodo quello delle cifre decimali che non si ripetono. La loro lunghezza è data dal numero di elementi di tali insiemi.
Un numero decimale periodico privo di anti-periodo si dice semplice, altrimenti è chiamato misto.
Una scrittura comoda per i numeri decimali periodici sta nel porre una linea sopra le cifre che si ripetono.
Se una frazione ha come denominatore un prodotto con fattori (anche) diversi da potenze di 2 o 5 allora esso si può convertire a decimale periodico. Per fare ciò estendiamo l' algoritmo di Euclide per la divisione tra numeri interi.
Algoritmo esteso di Euclide:
Dividere il numeratore per il denominatore con l' usuale algoritmo. Il quoziente è la parte intera.
Moltiplicare per 10 il resto ottenuto.
Spostarsi di una cifra decimale a destra. Nel caso in cui si calcoli la prima cifra decimale si frappone un punto (virgola) tra esso e la parte intera.
Dividere il nuovo resto per il denominatore con l' usuale algoritmo. Il quoziente è la cifra decimale.
Tornare all'istruzione 2.
Vediamo un esempio.
Esibiamo senza dimostrazione un criterio per poter prevedere il tipo di decimale associato ad una frazione ridotta:
Una frazione ridotta genera un numero decimale:
Limitato (o finito) se il denominatore è prodotto di potenze di 2 o 5
Periodico semplice se il denominatore è prodotto di potenze di primi diversi da 2 e 5
Periodico misto se il denominatore è prodotto di potenze di primi e di potenze di 2 o 5.
Qui si anticipano alcune operazioni tra numeri decimali che verranno spiegate nei paragrafi successivi.
La strategia si basa sul fatto di moltiplicare il decimale periodico per opportune potenze di 10 e sottrazioni.
Vediamo alcuni esempi.
Calcoliamo la frazione generatrice di un decimale periodico semplice.
Un frazione generatrice di un decimale periodico semplice ha per numeratore la differenza tra il decimale pensato senza virgole né linee e la parte intera, ed ha per denominatore un numero formato da cifre 9 tanti quanto la lunghezza del periodo.
Calcoliamo la frazione generatrice di un decimale periodico misto.
Un frazione generatrice di un decimale periodico misto ha per numeratore la differenza tra il decimale pensato senza virgole né linee e il numero intero formato dalle cifre non periodiche, ed ha per denominatore un numero formato da cifre 9 tanti quanto la lunghezza del periodo e tanti 0 quanto la lunghezza dell' anti-periodo.
Ampliamo le quattro operazioni aritmetiche ai decimali e moltiplichiamoli o dividiamoli per potenze di 10.
I decimali finiti sono i più facili da trattare perché funzionano allo stesso modo degli interi con qualche accortezza.
Per sommare o sottrarre due decimali finiti è sufficiente sommare le cifre sommando quelle più a destra e procedendo verso sinistra.
Nel caso il numero di cifre decimali non fosse lo stesso è sufficiente aggiungere tanti 0 in coda a quello che ne ha meno fino ad equipararli.
Vediamo alcuni esempi.
Moltiplicare decimali finiti è come la moltiplicazione di interi a più cifre, solo che il punto del prodotto va scritto partendo da destra la somma del numero di cifre decimali dei fattori.
Vediamo un esempio:
Moltiplicare o dividere un decimale finito è molto semplice: le cifre rimangono inalterate, ma il punto si sposta a destra o a sinistra un numero di posti uguale all'esponente.
Vediamo alcuni esempi.
Dividere decimali finiti è come la dividere interi a più cifre, infatti applicando la proprietà invariantiva della divisione si può moltiplicare dividendo e divisore per 10 al numero di cifre del decimale che ne possiede di più.
Operare con decimali periodici è possibile senza convertirli in frazioni, anche se il risultato si ottiene per approssimazioni successive e può risultare contro-intuitivo.
Prima di procedere con le operazioni vogliamo ricordare l' uguaglianza fondamentale tra numeri decimali:
Se un decimale periodico ha un periodo formato solo da 9 allora è possibile eliminarlo sommando 1 all' ultima cifra dell' anti-periodo.
Sommare o sottrarre decimali periodici si avvale delle stesse regole introdotte con i decimali finiti, ma si tratta di ripeterle più volte per capire la forma del risultato.
In generale è sufficiente calcolare tante somme o sottrazioni due volte quanto le cifre del periodo più lungo più una.
Vediamo un esempio.
Moltiplicare o dividere un decimale periodico è molto semplice: si scrive il numero per esteso e si sposta il punto come per i decimali finiti, poi si riscrive il decimale periodico in notazione compatta.
Vediamo alcuni esempi.
