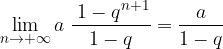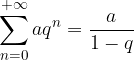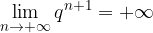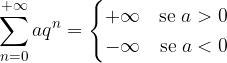Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





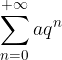
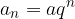
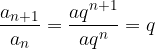
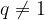 ) allora
) allora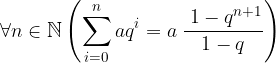
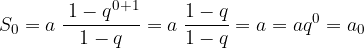 , quindi è verificato.
, quindi è verificato.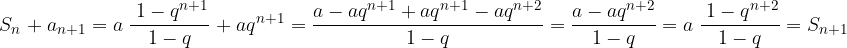
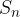 è la successione delle somme parziali di
è la successione delle somme parziali di 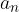 :
: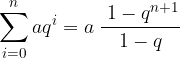
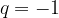
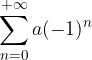
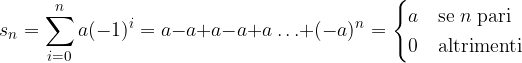
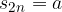
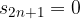
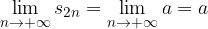
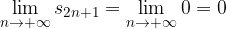
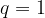
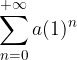
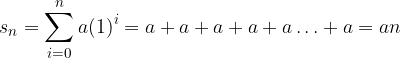
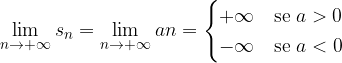
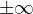 a seconda del segno di a.
a seconda del segno di a.
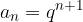 è infinitesima
è infinitesima