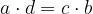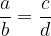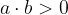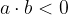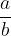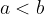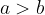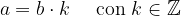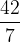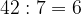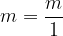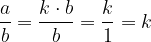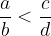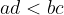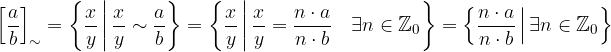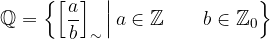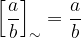L'operazione di divisione tra numeri interi non dà come risultato sempre un numero intero. Per questo motivo, ci serve introdurre i numeri frazionari, detti anche razionali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nella vita di tutti i giorni, usiamo spesso numeri interi e naturali. Ad esempio per:
contare le penne in un astuccio;
stilare un rendiconto finanziario elementare (spesa, ricavo, guadagno, perdita);
distribuire caramelle equamente ad un gruppo di persone;
Possiamo facilmente dividerci 20 caramelle quando siamo in 10. Ma cosa succede se siamo in 11? Per semplificare separiamo gli oggetti spezzabili, che sono utili anche quando vengono tagliati, da quelli che non lo sono.
Dobbiamo immaginare i numeri come oggetti spezzabili, per poter capire le frazioni.
Definizione di frazione
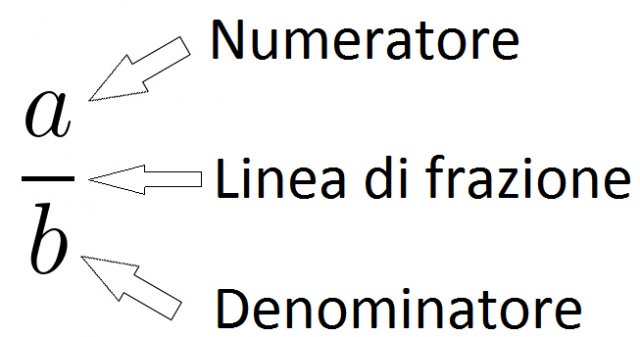
Una frazione è un numero della forma:
Altri modi per indicare una frazione sono a/b oppure a:b.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Possiamo pensare così: il denominatore indica in quante parti uguali un oggetto è stato diviso, mentre il numeratore quante di queste sono presenti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazioni equivalenti
Due frazioni 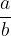 e
e 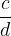 sono equivalenti se:
sono equivalenti se:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà invariantiva
Le frazioni godono di una proprietà fondamentale chiamata invariantiva. Tale proprietà è una generalizzazione della proprietà invariantiva della divisione tra numeri interi e ci permetterà di confrontare, sommare o sottrarre due frazioni.
Abbiamo visto quando due frazioni sono equivalenti o meno. Data una frazione 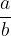 esiste un metodo per trovare altre frazioni equivalenti a quella data? Se sì, quante sono?
esiste un metodo per trovare altre frazioni equivalenti a quella data? Se sì, quante sono?
Data una frazione, è possibile ottenerne una equivalente moltiplicando o dividendo numeratore e denominatore per uno stesso numero intero non nullo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
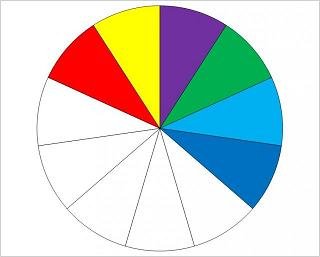
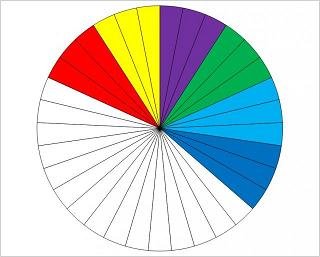
Un modo facile per capire la proprietà invariantiva è immaginarsi un oggetto spezzabile diviso in b parti uguali di cui ne abbiamo a.
Rappresentiamo la frazione:
Suddividiamo ogni settore (colorato o meno) in m parti:
Dato che la quantità non è variata le frazioni sono equivalenti.
Segno di una frazione
Come per i numeri interi, una frazione ha un segno: può essere positiva o negativa; tale segno è determinato dalla regola dei segni per il prodotto tra numeri interi.
Una frazione 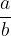 è positiva se
è positiva se 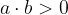
Una frazione 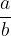 è negativa se
è negativa se 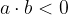
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Altri tipi di frazioni
Illustriamo alcuni insiemi di frazioni particolari.
Frazioni irriducibili
Una frazione 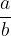 è irriducibile o ridotta ai minimi termini se MCD(a, b) = 1 ovvero il numeratore ed il denominatore sono coprimi.
è irriducibile o ridotta ai minimi termini se MCD(a, b) = 1 ovvero il numeratore ed il denominatore sono coprimi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Enunciamo una proprietà importante delle frazioni irriducibili.
Per ogni numero razionale esiste un'unica frazione irriducibile che lo rappresenti. In altre parole, di tutte le frazioni che rappresentano uno stesso numero razionale, ce n'è solo una irriducibile.
Cerchiamo di capire meglio con un esempio più concreto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazioni proprie
Una frazione si dice propria quando il numeratore è minore del denominatore.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazioni improprie
Una frazione si dice impropria se il numeratore è maggiore del denominatore.
Si dice impropria quando:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazioni apparenti
Una frazione si dice apparente se il numeratore è un multiplo del denominatore.
Si dice apparente quando:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
in realtà è una semplice divisione
il cui risultato è uguale a 6.
Interi come frazioni
I numeri razionali sono un'estensione dei numeri interi: per ogni intero dobbiamo trovare una frazione che lo identifichi.
Ogni numero intero m può essere identificato con una frazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per la proprietà invariantiva una frazione apparente:
si identifica con un numero intero.
Riassunto delle tipologie di frazioni
Dato che per due numeri interi distinti a e b si ha a < b oppure a > b concludiamo che:
frazioni che non sono proprie sono improprie;
frazioni che non sono improprie sono proprie;
frazioni apparenti sono improprie;
Confronto di numeri razionali
Come facciamo con i numeri interi, possiamo confrontare anche i numeri razionali; ovvero possiamo stabile se un numero razionale è maggiore o minore di un altro.
Date due frazioni 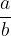 e
e 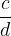 diciamo che:
diciamo che:
che assomiglia molto alla condizione di equivalenza, eccetto il simbolo di relazione.
Esiste un altro metodo per confrontare due frazioni:
Date due frazioni con il medesimo denominatore:
la prima frazione è minore della seconda se sono entrambe positive e il numeratore della prima frazione è minore del numeratore della seconda;
la prima frazione è minore della seconda se sono entrambe negative e il numeratore della prima frazione è maggiore del numeratore della seconda;
come per i numeri interi, frazioni positive sono sempre maggiori di quelle negative;
Per confrontare due frazioni è indifferente quale metodo si usa.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Retta razionale
Abbiamo visto in precedenza che i numeri razionali possono essere rappresentati tramite un cerchio (oggetto spezzabile) diviso in parti uguali tante quante il denominatore e prese in considerazione quante il numeratore.
Introduciamo qui un' altro tipo di rappresentazione.
Anche i numeri razionali, come i numeri interi, possono essere rappresentati su una retta numerica.
Tale retta includente i numeri razionali è chiamata retta razionale e può essere usata come metodo grafico per confrontare frazioni.
Ogni frazione corrisponde ad un solo punto sulla retta razionale.
Definizione di numero razionale
Questo paragrafo è destinato agli studenti che desiderano approfondire la teoria che sta alla base del concetto di numero razionale.
L' insieme delle sue frazioni equivalenti è:
che chiamiamo classe di equivalenza della frazione. La frazione 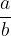 si chiama rappresentante della classe.
si chiama rappresentante della classe.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Abbiamo visto che - data una frazione - la quantità che essa rappresenta rimane invariata se applichiamo la proprietà invariantiva. Data una classe di equivalenza non è importante quale rappresentante si prenda in quanto varieranno solamente le suddivisioni in cui la quantità è stata divisa.
L'insieme di tali quantità a meno della proprietà invariantiva compongono l'insieme dei numeri razionali**
A questo punto sorgono alcune lecite domande:
Tale insieme è ben definito?
Ci possono essere due frazioni non equivalenti che rappresentano lo stesso numero razionale?
Due classi di equivalenza diverse sono disgiunte?
Due classi di equivalenza sono uguali se e solo se i rappresentanti sono equivalenti?
Per rispondere affermativamente a tutte queste domande logicamente equivalenti è sufficiente prendere due classi di equivalenza uguali con diverso rappresentante e mostrare che i rappresentanti sono equivalenti.
Per non appesantire la notazione scriveremo con un abuso di linguaggio
Quindi quando diremo che due frazioni sono uguali in realtà stiamo uguagliando le loro classi di equivalenza ovvero stiamo omettendo che i due rappresentanti sono equivalenti.





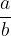 e
e 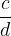 sono equivalenti se:
sono equivalenti se: