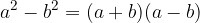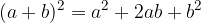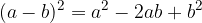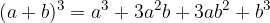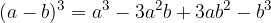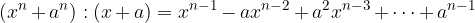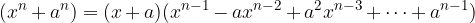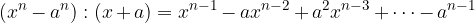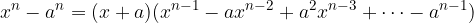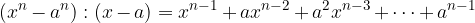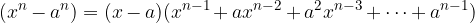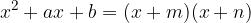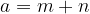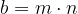La scomposizione si può considerare come il procedimento inverso alla moltiplicazione: leggiamo i numeri e le lettere che compongono un polinomio come i risultati di moltiplicazioni già fatte.
Dobbiamo imparare a percorrere a rovescio le moltiplicazioni.
La scomposizione di un polinomio in fattori è quindi la procedura attraverso cui riusciamo ad abbassare il grado di un polinomio, senza cambiare il suo valore.
Facciamo un esempio semplice:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Raccoglimento a fattor comune
Se i monomi che fanno parte di un polinomio sono divisibili per lo stesso monomio, possiamo raccogliere a fattor comune o mettere in evidenza tale monomio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Differenza di due quadrati
Differenza di due quadrati
Possiamo scomporre in fattori un polinomio che sia la differenza di due quadrati.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trinomio equivalente al quadrato di un binomio
Quadrato di un binomio somma
Quadrato di un binomio differenza
il quadrato del primo monomio;
il quadrato del secondo monomio;
il doppio prodotto dei due monomi;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quadrinomio equivalente al cubo di un binomio
Cubo di un binomio differenza
due monomi che sono cubi;
da altri due monomi che sono ognuno il triplo prodotto del quadrato dell'uno per l'altro;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma e differenza di potenze di uguale grado
Per n dispari
Quoziente tra la somma di due potenze di grado n e il corrispondente binomio somma di primo grado:
E quindi vale anche l'uguaglianza:
Svolgimento della somma di due potenze di grado n, con n dispari:
Possiamo scomporre in questo modo la somma di potenze uguali con esponente dispari.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per n pari
Quoziente tra la differenza di due potenze di grado n e il corrispondente binomio somma di primo grado
E quindi vale anche l'uguaglianza:
Svolgimento della differenza di due potenze di grado n, con n pari:
Possiamo scomporre in questo modo la differenza di potenze uguali con esponente pari.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per qualsiasi n
Quoziente tra la differenza di due potenze di grado n e il corrispondente binomio differenza di primo grado
per qualunque valore di n
E quindi possiamo anche scrivere:
Svolgimento della differenza di due potenze di grado n, con n qualsiasi
Possiamo scomporre in questo modo la differenza di potenze uguali, qualunque sia il valore dell'esponente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trinomio di secondo grado
Se in un trinomio di secondo grado nella variabile x:
il secondo coefficiente è uguale alla somma di due numeri relativi;
il terzo coefficiente è uguale al prodotto tra quei due stessi numeri;
Allora il trinomio di secondo grado è uguale al prodotto (x + 1° numero) (x + 2° numero)
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Scomposizione di un trinomio di secondo grado
Un trinomio di secondo grado è scomponibile come segue:
Scomposizione tramite la Regola di Ruffini
Possiamo vedere qui che, se un polinomio viene annullato sostituendo alla sua variabile un numero relativo k, tale polinomio è divisibile per il binomio (x - k).
Se tale polinomio ha più zeri o radici, ovvero più numeri che lo rendono uguale a zero, allora tale polinomio è divisibile per tanti binomi (x - k) in cui possiamo sostituire di volta in volta a k ognuno dei numeri che annullano il polinomio dato.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Come possiamo notare dall'esempio, 3 e -5 sono anche entrambi divisori del termine noto del polinomio iniziale, ovvero di -15. Ne deduciamo che:
Regola per la ricerca degli zeri di un polinomio
Gli zeri di un polinomio sono divisori del suo termine di grado zero.
Possiamo dunque cercare gli zeri di un polinomio tra tutti i divisori del termine noto per poi scartare quelli che non annullano il polinomio.
Infatti, nell'esempio, divisori di -15 sono +3, -3, +5 e -5, ma come abbiamo visto solo +3 e -5 annullano il polinomio e quindi sono suoi zeri.
Dividendo così un polinomio per ognuno dei binomi per cui esso è divisibile, possiamo ottenere via via dei polinomi più semplici, il cui prodotto ci dà proprio il polinomio di partenza. Se svolgiamo quindi divisioni successive con la Regola di Ruffini, possiamo scomporre in fattori un polinomio complesso.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Utilizzo di artifici
Nel processo di scomposizione in fattori di un polinomio, a volte dobbiamo ricorrere a degli artifici. Consideriamo i seguenti esempi:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per differenze di potenze di ugual grado e superiori a 2, procediamo considerandole differenze di quadrati come mostrato nell'esempio seguente:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per somme di potenze di ugual grado con esponente divisibile per 3, possiamo procedere considerandole somme di cubi come mostrato nell'esempio seguente:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
M.C.D. e m.c.m. di polinomi
Il Massimo Comun Divisore o M.C.D. di polinomi scomposti in fattori e non ulteriormente scomponibili è dato dal prodotto dei fattori comuni, ciascuno preso col minor esponente.
Il minimo comune multiplo o m.c.m. di polinomi scomposti in fattori e non ulteriormente scomponibili è dato dal prodotto dei fattori comuni e non comuni, ciascuno preso una sola volta e col maggior esponente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il M.C.D. e il m.c.m di due o più polinomi interi in una stessa variabile si possono calcolare con il cosiddetto metodo Euclideo delle divisioni successive:
Per il M.C.D. di due polinomi interi nella stessa variabile, procediamo dividendo il polinomio di grado maggiore per quello di grado minore. Dividiamo poi il polinomio di grado minore per il resto della prima divisione. Dividiamo il primo resto per il secondo resto e così via fino ad ottenere per resto zero o un'espressione di grado zero rispetto alla variabile.
Quando il resto finale è zero, il M.C.D. è dato dal penultimo resto. Quando il resto finale è un'espressione di grado zero rispetto alla variabile, allora i due polinomi iniziali sono primi fra loro.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per il m.c.m. di due polinomi interi nella stessa variabile, procediamo moltiplicando uno di essi per il quoziente della divisione tra l'altro polinomio e il loro M.C.D.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »