Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





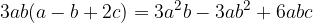
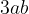 , nell'esempio), tale polinomio equivale al prodotto del divisore comune per il polinomio i cui monomi sono dati dal quoziente dei suoi termini per il divisore comune.
, nell'esempio), tale polinomio equivale al prodotto del divisore comune per il polinomio i cui monomi sono dati dal quoziente dei suoi termini per il divisore comune.