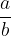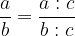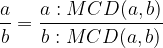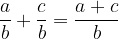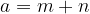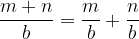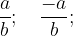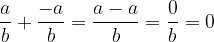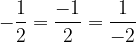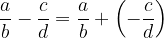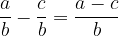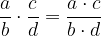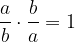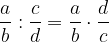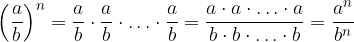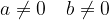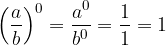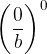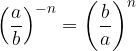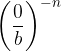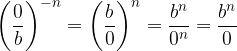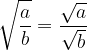Come tra i numeri interi, possiamo fare una serie di operazioni matematiche tra i numeri razionali. Oltre alle operazioni di base come somma, sottrazione, moltiplicazione, divisione e potenze, ci sono alcune operazioni particolari dei numeri razionali. Cominciamo con una di queste, la semplificazione.
Semplificazione
La semplificazione ci permette di trasformare una frazione con numeratore e denominatore grandi, in una frazione equivalente con numeratore e denominatore più piccoli.
Consideriamo una frazione:
Senza che cambi il valore della frazione possiamo dividere il numeratore e il denominatore per un loro divisore comune, grazie alla proprietà invariantiva:
Per semplificare una frazione, dividiamo il numeratore ed il denominatore per il loro divisore comune più grande, il massimo comun divisore. Otteniamo una frazione equivalente a quella data, ma più semplice:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Addizione
Eseguiamo la somma tra due frazione in modo diverso se hanno lo stesso denominatore o se hanno due denominatori diversi. Vediamo i due casi.
Stesso denominatore
La somma di due frazioni con lo stesso denominatore è uguale a:
La somma di due frazioni con lo stesso denominatore è uguale ad una frazione con:
Il numeratore è la somma dei numeratori dati.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Denominatore diverso
Nel caso di frazioni con denominatori diversi, dobbiamo trasformarle in frazioni con lo stesso denominatore, sfruttando la proprietà invariantiva. Le frazioni con denominatore comune devono essere equivalenti a quelle di partenza. Per convenienza, prendiamo il minimo comune multiplo tra i denominatori, chiamato minimo comune denominatore. Può essere abbreviato con m.c.d.
Vediamo come funziona tramite un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dissociazione
Dissociare una frazione significa scriverla come somma di due o più frazioni.
Esprimiamo il numeratore come somma di due numeri interi:
Sostituiamo ed applichiamo la definizione di addizione tra frazioni
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazione opposta
Introduciamo il concetto di frazione opposta, che è legato alla somma. La somma tra una frazione e la sua opposta risulta zero.
Due frazioni opposte sono:
Infatti se le sommiamo otteniamo 0:
L'opposta di una frazione è una frazione con numeratore e denominatore uguali a quelli dati, a meno del segno di uno dei due.
Possiamo mettere il segno meno in tre posizioni, senza cambiare il significato di una frazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sottrazione
Definiamo la sottrazione a partire dalla sottrazione, come per i numeri interi. Possiamo pensare alla sottrazione tra due frazioni come alla somma tra la prima frazione e l'opposta della seconda.
La sottrazione tra frazioni è quindi uguale alla somma tra frazioni. Anche qui dobbiamo fare attenzione al denominatore delle frazioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Moltiplicazione
Il loro prodotto di due frazioni è:
Il prodotto di due frazioni è una frazione che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denominatori.
Il segno segue la regola dei segni introdotta con i numeri interi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nella moltiplicazione è possibile semplificare una frazione con l'altra.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Frazione reciproca o inversa
Nell'ambito della moltiplicazione tra frazioni, introduciamo il concetto di frazione reciproca. Il prodotto tra una frazione e la sua reciproca risulta uno.
Consideriamo una frazione:
La reciproca di una frazione è una frazione che ha numeratore e denominatore scambiati.
Infatti se le moltiplichiamo otteniamo 1:
Una frazione che ammetta reciproca si dice invertibile.
Non è invertibile perché la sua reciproca:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione
Possiamo definire la divisione tra frazioni a partire dalla moltiplicazione. La divisione tra due frazioni è infatti una moltiplicazione, ma dobbiamo moltiplicare la prima frazione con il reciproco della seconda frazione.
La divisione tra due frazioni è il prodotto della prima con il reciproco della seconda. La regola per i segni è la stessa della moltiplicazione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Potenze di Frazioni
In questo capitolo cercheremo di definire le potenze di frazioni cercando di mantenere ed estendere le proprietà che esse avevano per i numeri interi.
Esponente intero positivo
Calcoliamo la potenza n-esima di una frazione, con n intero positivo:
Applichiamo la regola di moltiplicazione per frazioni n volte:
La potenza di una frazione con esponente intero positivo è una frazione che ha per numeratore la potenza n-esima del numeratore dato e per denominatore la potenza n-esima del denominatore dato.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esponente nullo
Merita una discussione a parte la frazione non nulla elevata alla 0:
La potenza di esponente 0 di una frazione non nulla è 1.
Non ha significato in quanto:
Esponente intero negativo
La potenza n-esima di una frazione con n intero negativo è una frazione che ha per base l'inversa della frazione di partenza ed esponente opposto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La frazione con numeratore nullo elevata ad esponente negativo:
Non ha significato, perché equivale ad una frazione con denominatore nullo:
Radice di una frazione
Per la radice della frazioni rimandiamo alla sezione sui radicali. In generale, vale la regola:
Espressioni con Frazioni
Abbiamo già visto con i numeri interi quali sono le regole per calcolare il risultato di più operazioni tra di essi. Tali regole rimangono valide per le frazioni.
In un'espressione con frazioni l'ordine delle operazioni è:
moltiplicazioni e divisioni;
L'ordine delle parentesi è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »