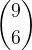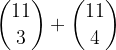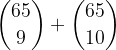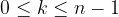Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





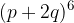
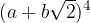
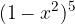
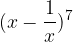
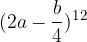
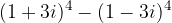
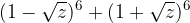
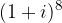
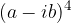
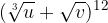
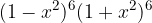

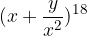
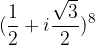
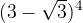
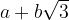 , con
, con 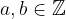 .
.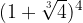
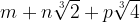 , dove
, dove 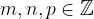 .
.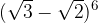
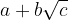 , dove
, dove 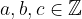 .
.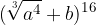
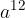
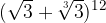
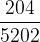
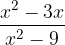
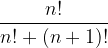
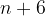 ,
,  ,
,  costituiscano una progressione geometrica ?
costituiscano una progressione geometrica ?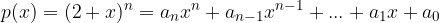 . Che valore deve assumere n (n > 1) perché i coefficienti
. Che valore deve assumere n (n > 1) perché i coefficienti 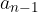 e
e 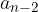 del polinomio siano uguali tra loro ?
del polinomio siano uguali tra loro ?