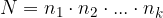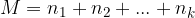Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





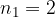 (nera o blu),
(nera o blu),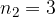 (nera, bianca o rossa)
(nera, bianca o rossa)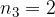 (nere o rosse).
(nere o rosse).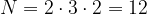
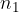 elementi a disposizione,
elementi a disposizione,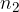 elementi a disposizione,
elementi a disposizione,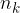 elementi a disposizione.
elementi a disposizione. ) che abbiamo a disposizione ad ogni fase:
) che abbiamo a disposizione ad ogni fase: