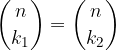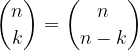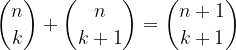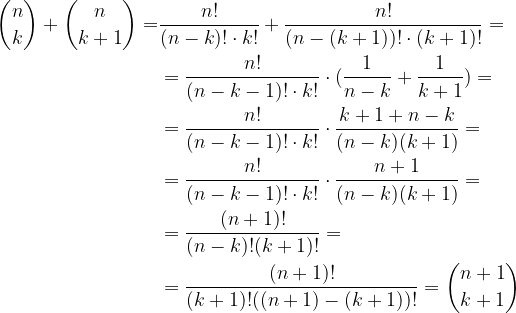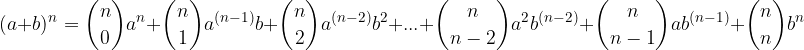Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





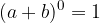
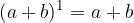
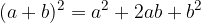
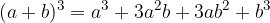
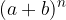
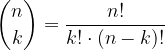
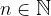 vale:
vale: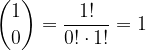
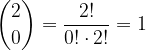
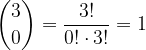

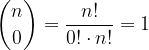
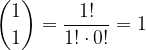
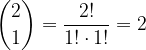
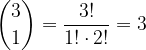
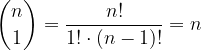
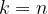 :
: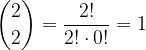
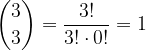
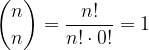
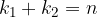 , da cui:
, da cui: