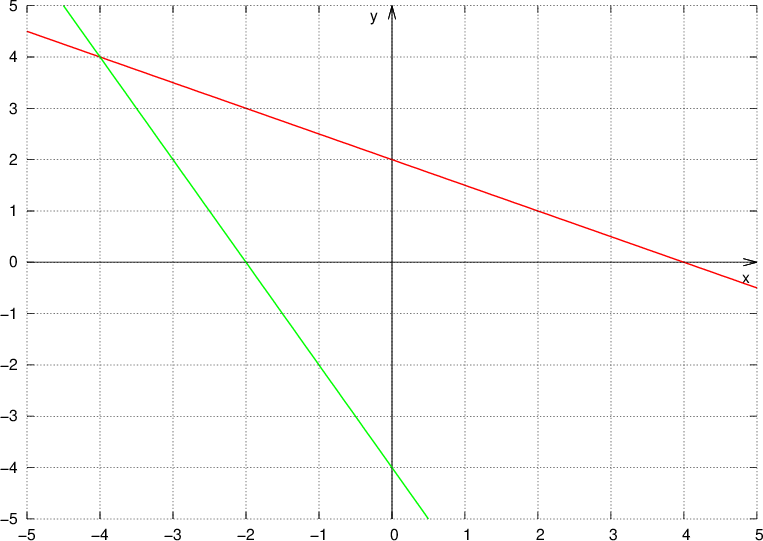
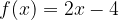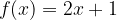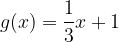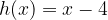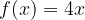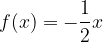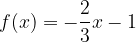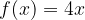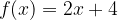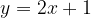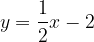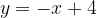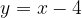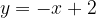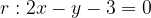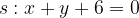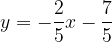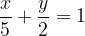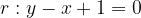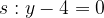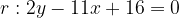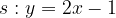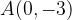Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




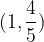 e
e 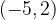
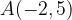 e
e 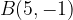
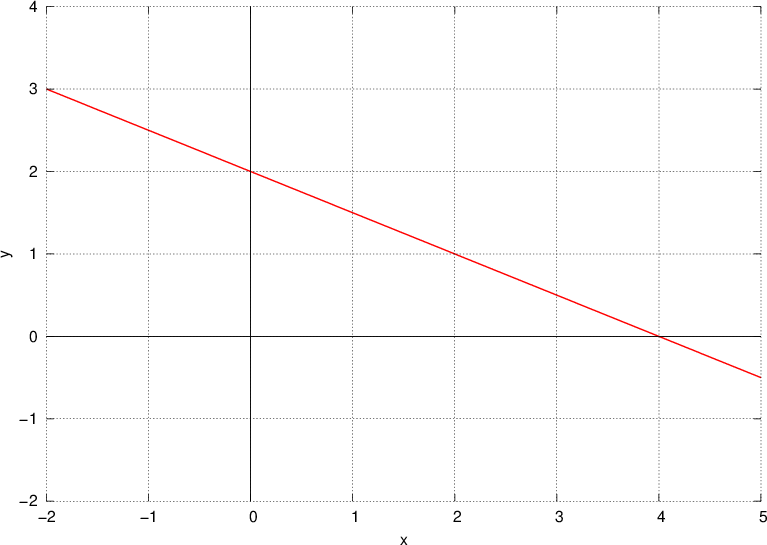
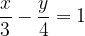
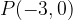 e che ha intercetta
e che ha intercetta 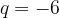 .
.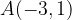 ,
, 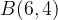 e
e 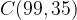 si trovano sulla stessa retta. Giustificare la risposta.
si trovano sulla stessa retta. Giustificare la risposta.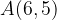
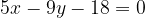
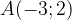 e
e 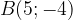 , calcolare:
, calcolare: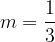 e che passa per il punto T(3,-1).
e che passa per il punto T(3,-1).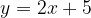
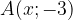
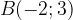
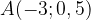 ,
, 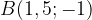 ,
, 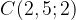
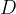 .
.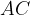 del rettangolo.
del rettangolo.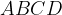 .
.