Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




 e
e  , per stabilire la loro posizione reciproca possiamo procedere in due modi:
, per stabilire la loro posizione reciproca possiamo procedere in due modi: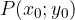 devono essere soluzione di entrambe le equazioni, quindi per ottenerle risolviamo il seguente sistema:
devono essere soluzione di entrambe le equazioni, quindi per ottenerle risolviamo il seguente sistema: