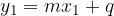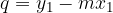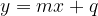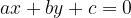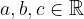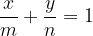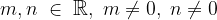Richiamiamo innanzitutto questi concetti:
la retta è un ente geometrico fondamentale, del quale abbiamo un'idea intuitiva; una proprietà caratteristica di tutti e soli i punti del piano cartesiano che appartengono a una retta è il fatto che sono infiniti punti allineati.
Per disegnare le rette sul piano cartesiano consideriamo equazioni in due variabili, indicate generalmente come x e y:
Le soluzioni di un'equazione lineare nelle variabili x e y sono delle coppie di numeri reali 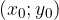 che la soddisfano, ossia tali che
che la soddisfano, ossia tali che 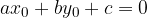 .
.
Possiamo vedere tali coppie di numeri come punti del piano cartesiano.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un importante teorema afferma che:
le soluzioni di ogni equazione lineare in due variabili sono le coordinate dei punti di una retta;
ogni retta nel piano cartesiano si può scrivere come luogo geometrico dei punti che soddisfano un'equazione lineare in due variabili.
Corrispondenza tra rette sul piano cartesiano e equazioni lineari.
A ogni retta del piano cartesiano corrisponde un'equazione lineare in due variabili e, viceversa, a ogni equazione lineare in due variabili corrisponde una retta del piano cartesiano.
Vediamo alcuni casi di retta sul piano cartesiano e ne determiniamo l'equazione lineare corrispondente.
Rette parallele agli assi
Vediamo il caso di una retta parallela all'asse x e di una parallela all'asse y.
Asse x
Vediamo l'equazione di una retta parallela all'asse delle ascisse, partendo da un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Possiamo fare le stesse considerazioni per una qualsiasi retta parallela all'asse x passante per un punto 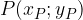 : essa avrà equazione della forma
: essa avrà equazione della forma
dove k è una costante, uguale a 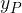 .
.
Asse y
Vediamo ora un esempio di retta parallela all'asse y.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Possiamo fare le stesse considerazioni per una qualsiasi retta parallela all'asse y passante per un punto 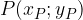 : essa avrà equazione della forma
: essa avrà equazione della forma
dove h è una costante, uguale a 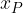 .
.
Rette passanti per l'origine
Vediamo ora quale equazione è associata a una retta passante per l'origine.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nell'esempio precedente osserviamo che il coefficiente della x, 2, è ottenuto come rapporto fra l'ordinata e l'ascissa del punto P. Questo rapporto rappresenta la pendenza della retta passante per P e per O.
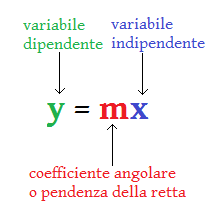
L'equazione di una retta passante per l'origine è della forma
dove m è un numero reale che viene chiamato coefficiente angolare.
Il numero m rappresenta la pendenza della retta.
Equazione di una retta generica
Per trovare l'equazione di una generica retta ci rifacciamo al caso della retta passante per l'origine, alla quale applichiamo una traslazione.
Il procedimento consiste nel traslare la retta passante per due punti 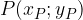 e
e 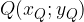 spostandola in alto o in basso fino a farla passare per l'origine. Una volta scritta l'equazione di questa retta, la si riporta alla posizione originale con la traslazione inversa.
spostandola in alto o in basso fino a farla passare per l'origine. Una volta scritta l'equazione di questa retta, la si riporta alla posizione originale con la traslazione inversa.
Vediamolo in pratica, con un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
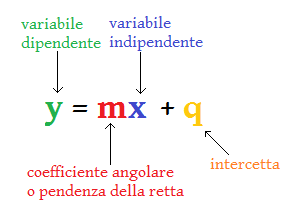
Una retta generica, non verticale, ha un'equazione della forma
dove m e q sono due parametri reali.
Questa si chiama retta scritta in forma esplicita.
m è il coefficiente angolare della retta, che ne quantifica la pendenza.
m si ottiene a partire dalle coordinate di due punti qualsiasi appartenenti alla retta 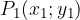 e
e 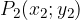 , calcolando
, calcolando
q è l'intercetta, ossia l'ordinata del punto di intersezione della retta con l'asse y.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazione implicita di una retta
Possiamo riscrivere l'equazione
in un altra forma più generale, che ci consente di considerare anche le rette verticali, che restavano escluse nel paragrafo precedente.
Una retta in forma implicita è descritta da un'equazione della forma:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Forma segmentaria della retta
Le equazioni di rette non parallele ad uno dei due assi e non passanti per l'origine, possono essere scritte in un altro modo.
La retta interseca l'ascissa nel punto A(m; 0) e l'asse delle ordinate nel punto B(0; n). Conoscendo questi due punti, siamo in grado di scrivere l'equazione nella forma segmentaria della retta.
Forma segmentaria della retta:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




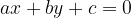
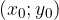 che la soddisfano, ossia tali che
che la soddisfano, ossia tali che 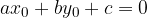 .
.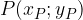 : essa avrà equazione della forma
: essa avrà equazione della forma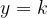
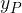 .
.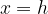
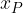 .
.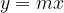
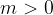 la retta è crescente: all'aumentare dell'ascissa x aumenta anche il valore dell'ordinata y. In questo caso (vedi per esempio il caso
la retta è crescente: all'aumentare dell'ascissa x aumenta anche il valore dell'ordinata y. In questo caso (vedi per esempio il caso 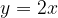 svolto prima) la retta passa per il primo e il terzo quadrante.
svolto prima) la retta passa per il primo e il terzo quadrante.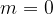 ritroviamo l'equazione
ritroviamo l'equazione 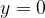 , che rappresenta l'asse x.
, che rappresenta l'asse x.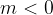 la retta è decrescente: all'aumentare di x il valore dell'ordinata y diminuisce. In questo caso la retta passa per il secondo e il quarto quadrante.
la retta è decrescente: all'aumentare di x il valore dell'ordinata y diminuisce. In questo caso la retta passa per il secondo e il quarto quadrante.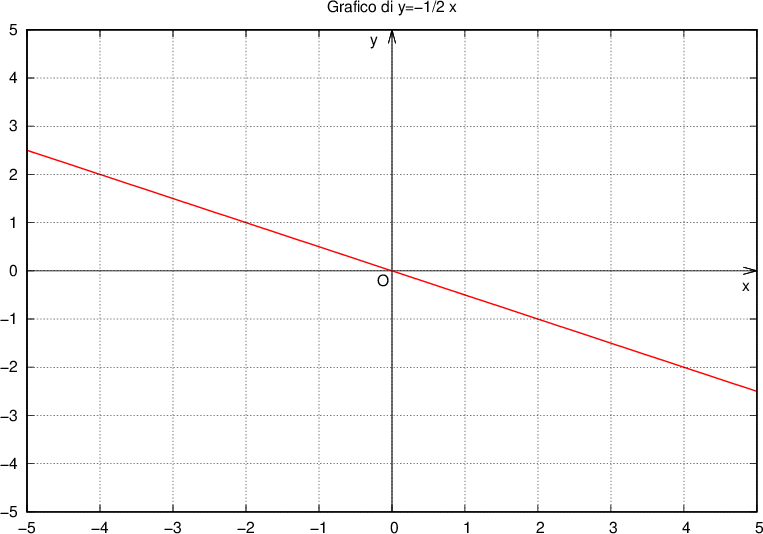
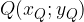 spostandola in alto o in basso fino a farla passare per l'origine. Una volta scritta l'equazione di questa retta, la si riporta alla posizione originale con la traslazione inversa.
spostandola in alto o in basso fino a farla passare per l'origine. Una volta scritta l'equazione di questa retta, la si riporta alla posizione originale con la traslazione inversa.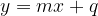
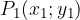 e
e 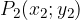 , calcolando
, calcolando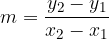
 o
o 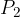 : ad esempio
: ad esempio