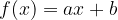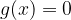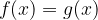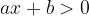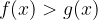Tutte le equazioni di primo grado si possono risolvere anche in modo grafico! Un'equazione di primo grado è in realtà una retta sul piano cartesiano.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il piano cartesiano
Il piano cartesiano è un sistema di riferimento formato da due rette ortogonali (asse 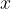 e asse
e asse 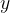 ) che si intersecano in un punto chiamato origine. Su ciascuna retta si fissa un orientamento ed un'unità di misura.
) che si intersecano in un punto chiamato origine. Su ciascuna retta si fissa un orientamento ed un'unità di misura.
La rappresentazione grafica di rette sul piano cartesiano segue alcune precise proprietà:
Retta verticale
La rappresentazione grafica di una funzione del tipo
dove 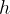 è una costante, è una retta parallela all’asse delle
è una costante, è una retta parallela all’asse delle 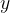 ;
;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Retta orizzontale
La rappresentazione grafica di una funzione del tipo
dove 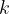 è una costante, è una retta parallela all’asse delle
è una costante, è una retta parallela all’asse delle 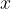 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Retta generica
La rappresentazione grafica di una funzione del tipo
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Rappresentazione grafica delle equazioni di primo grado
Abbiamo due membri dell'equazione, uno a sinistra e uno a destra dell'uguale. Andiamo disegnarli sul piano cartesiano. 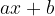 è una funzione e
è una funzione e 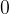 è un'altra funzione.
è un'altra funzione.
Andiamo quindi a vedere quando le due funzioni si incrociano sul piano cartesiano e troviamo il corrispondente valore di x. Troviamo dunque quando:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
E’ interessante considerare i casi delle equazioni impossibili e indeterminate:
Per le equazioni impossibili il grafico sarà formato da due rette parallele, che non si incontrano mai.
Per le equazioni indeterminate invece avremo due rette coincidenti.
Equazione impossibile
Vediamo il caso di un'equazione impossibile tramite un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dunque nessun valore della x soddisfa l'uguaglianza, quindi l'equazione è IMPOSSIBILE.
Equazione indeterminata
Vediamo il caso di un'equazione indeterminate tramite un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dunque qualsiasi valore della x soddisfa l'uguaglianza, quindi l'equazione è INDETERMINATA.
Rappresentazione grafica delle disequazioni di primo grado
Abbiamo due membri dell'equazione, uno a sinistra e uno a destra dell'uguale. Andiamo disegnarli sul piano cartesiano. 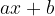 è una funzione e
è una funzione e 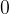 è un'altra funzione.
è un'altra funzione.
Andiamo quindi a vedere quando la prima funzione è maggiore della seconda e troviamo il corrispondente valore di x. Troviamo dunque quando:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





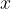 e asse
e asse 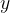 ) che si intersecano in un punto chiamato origine. Su ciascuna retta si fissa un orientamento ed un'unità di misura.
) che si intersecano in un punto chiamato origine. Su ciascuna retta si fissa un orientamento ed un'unità di misura.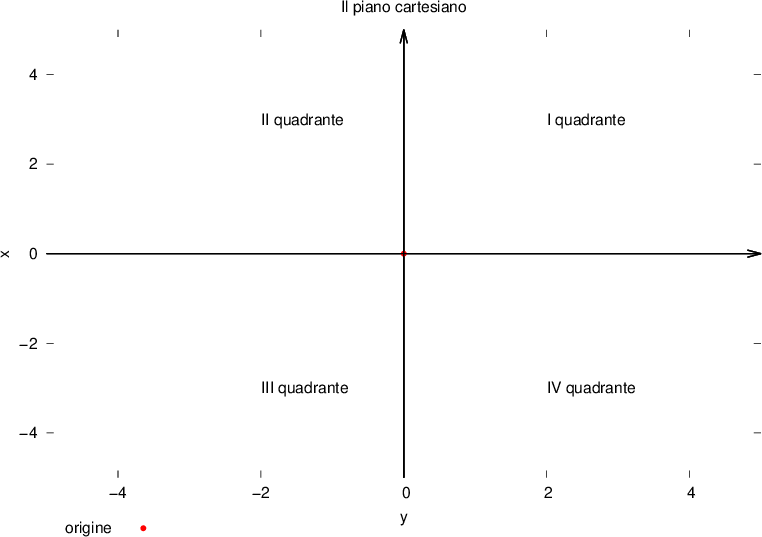
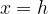
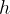 è una costante, è una retta parallela all’asse delle
è una costante, è una retta parallela all’asse delle 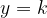
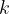 è una costante, è una retta parallela all’asse delle
è una costante, è una retta parallela all’asse delle 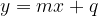
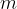 rappresenta il coefficiente angolare ed esprime la pendenza della mentre
rappresenta il coefficiente angolare ed esprime la pendenza della mentre 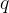 viene detta intercetta e rappresenta l’ordinata del punto di intersezione della retta con l’asse
viene detta intercetta e rappresenta l’ordinata del punto di intersezione della retta con l’asse 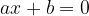
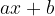 è una funzione e
è una funzione e 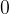 è un'altra funzione.
è un'altra funzione.