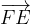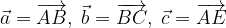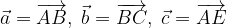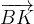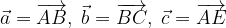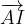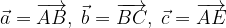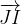Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





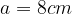 e
e 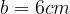 . Sia E un punto del lato AD tale che
. Sia E un punto del lato AD tale che  .
. in funzione del vettore
in funzione del vettore 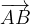 .
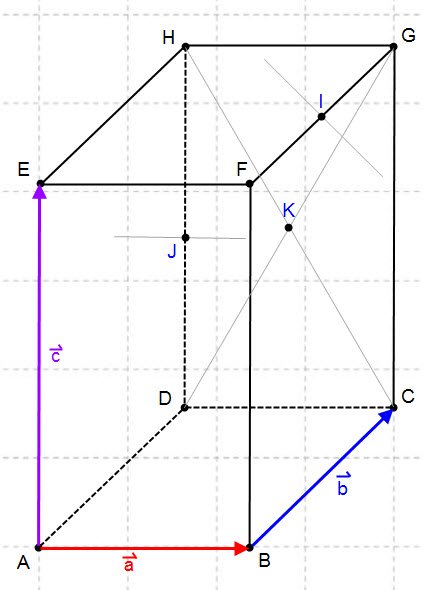
.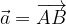 e
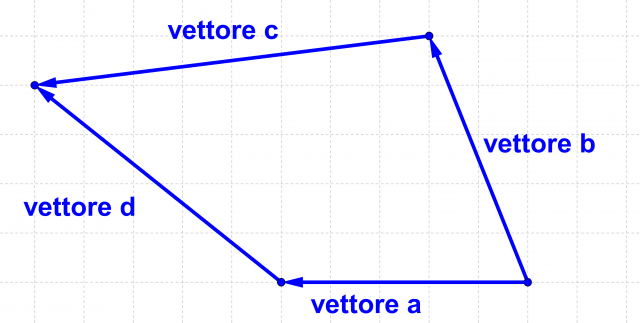
e 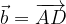 calcolare i vettori:
calcolare i vettori: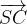
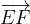
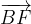
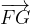
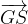
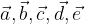 ed
ed 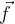 scriverli tutti in funzione di
scriverli tutti in funzione di 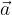 e
e 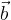 .
.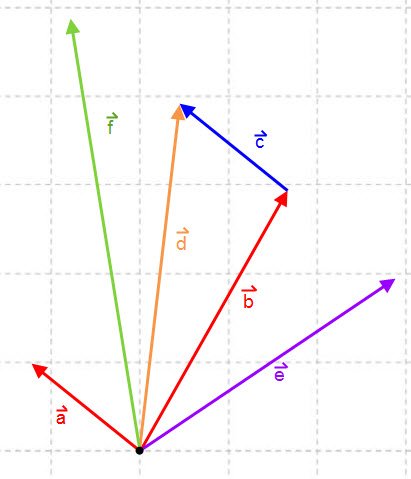
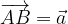 e
e  calcolare i vettori:
calcolare i vettori:
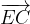
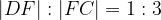 . Noti i vettori:
. Noti i vettori: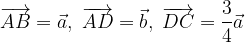
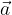 e
e 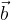 i vettori:
i vettori: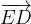
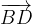
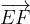
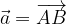
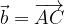
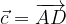
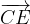
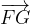
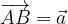 ed
ed 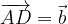 , dimostrare che il vettore
, dimostrare che il vettore 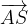 corrisponde a metà della diagonale
corrisponde a metà della diagonale 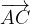 .
.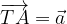 e
e 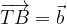 , dimostrare che
, dimostrare che 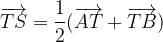 .
.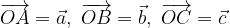 .
. .
.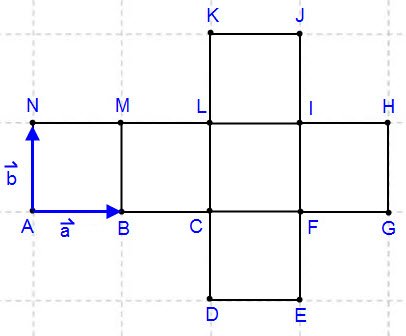
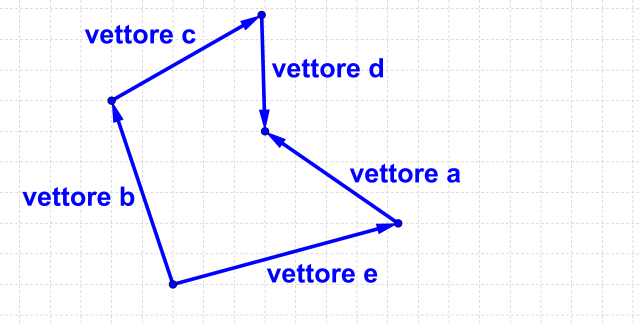
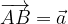 e
e 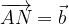 trovare i seguenti vettori:
trovare i seguenti vettori: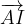
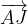
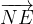
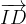
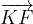
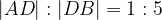 , mentre E è un punto del lato BC tale che
, mentre E è un punto del lato BC tale che 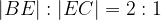 . Sia F il punto in cui si intersecano i lati AE e DC. Trovare il rapporto
. Sia F il punto in cui si intersecano i lati AE e DC. Trovare il rapporto 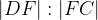 .
.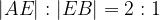
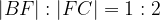

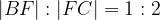
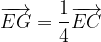
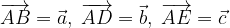
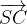
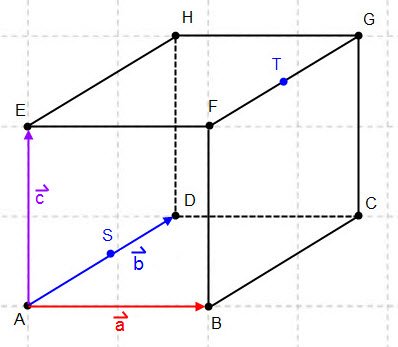
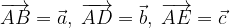
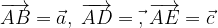
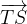

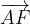
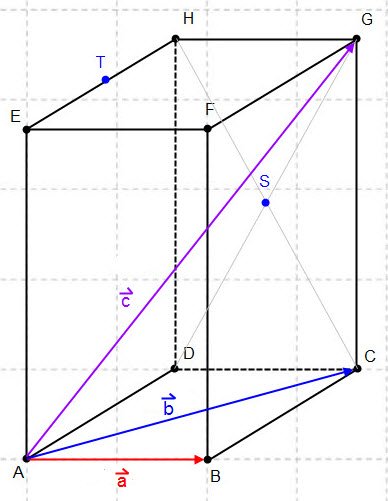
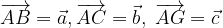
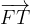
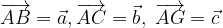
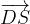
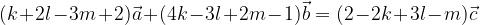
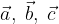
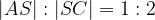
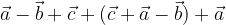
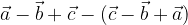
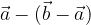
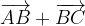
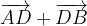
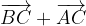
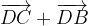
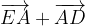
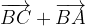
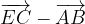
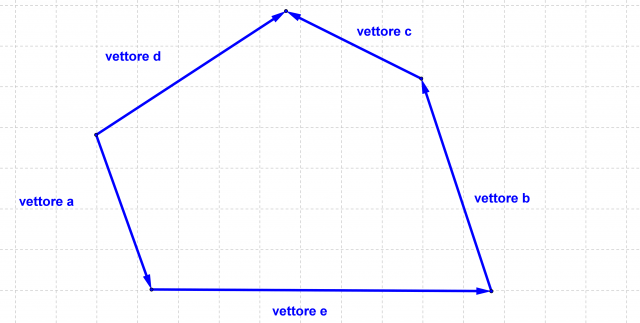
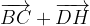
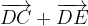
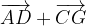
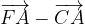
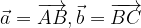 e
e 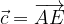 scrivere il vettore
scrivere il vettore 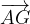 .
.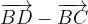

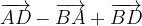
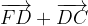
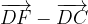
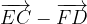
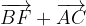
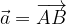
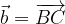
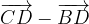
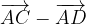

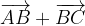
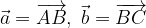
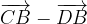
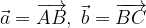
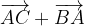
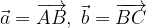
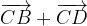
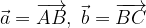
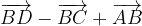
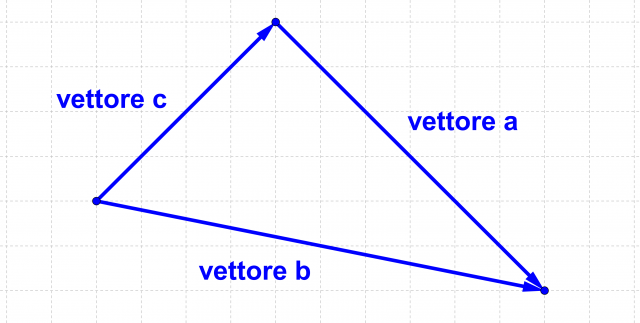
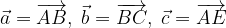
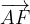
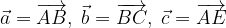
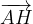
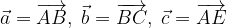
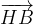
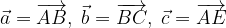
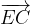
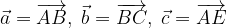
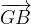
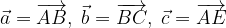
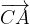

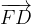
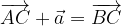
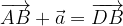
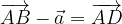
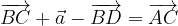
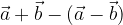 .
.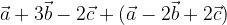
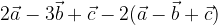
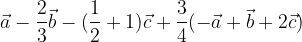
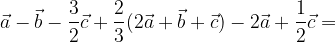
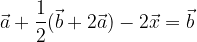
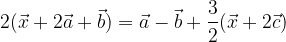
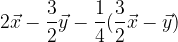
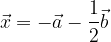
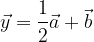
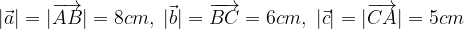
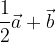
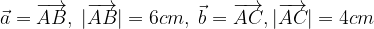
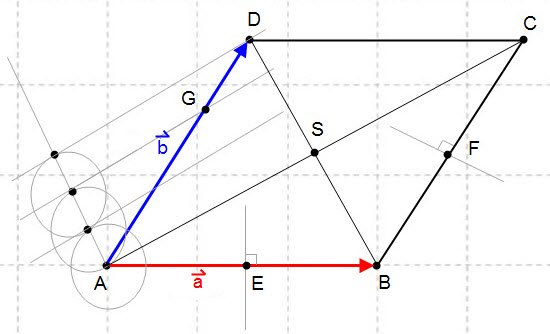
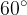 . Trovare i punti D, E ed S in modo che:
. Trovare i punti D, E ed S in modo che:
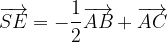
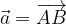 e
e 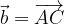 . Dimostrare che il segmento DE è la metà di AB.
. Dimostrare che il segmento DE è la metà di AB.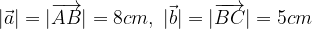
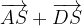 e
e 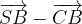 , esprimendo tutto in funzione dei vettori
, esprimendo tutto in funzione dei vettori 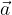 e
e 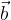
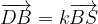
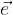 relativo al vettore
relativo al vettore 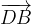
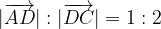
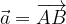 e
e 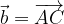 esprimere i vettori:
esprimere i vettori: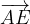
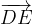
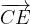
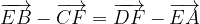
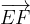 in funzione degli altri vettori e dimostrare che è parallelo alle basi e passante per il punto medio dei lati obliqui.
in funzione degli altri vettori e dimostrare che è parallelo alle basi e passante per il punto medio dei lati obliqui.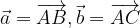 e
e 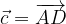 esprimere il vettore
esprimere il vettore