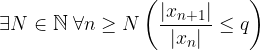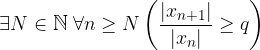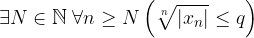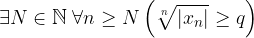Uno dei più noti paradossi dell'antichità era Achille e la Tartaruga ideato da Zenone di Elea (489 - 431 A.C.).
Achille - simbolo della rapidità greca - deve raggiungere la tartaruga - sinonimo di lentezza. Achille corre più svelto della tartaruga e le concede dieci metri di vantaggio. Achille - percorsi i dieci metri - raggiunge la posizione iniziale della tartaruga, ma essa nel frattempo s'è mossa - per quanto lentamente - e si trova un po' più avanti di Achille. Ogniqualvolta Achille provi a colmare la distanza tra lui e la tartaruga, essa - per quanto poco - avanza. Concludiamo che Achille non raggiungerà mai la Tartaruga.
La nascita di questo paradosso è dovuta al modo di pensare greco: sommando un'infinita di numeri si ottiene infinito. In questo capitolo introdurremmo gli strumenti matematici necessari per comprendere e risolvere il problema suddetto.
Definizione
Prima di arrivare alla definizione, introduciamo le seguenti scritture intuitive per indicare una somma con infiniti addendi:
Chiameremo tali oggetti matematici serie numeriche.
Riprendiamo con la definizione.
Siamo capaci di sommare solo un numero finito di volte, quindi la strada più intuitiva e semplice per poter "sommare" un numero infinito di volte è definire una successione che mappa il numero degli addendi nella loro somma:
Man mano che l'indice - il numero degli addendi - aumenterà arbitrariamente, saremo sempre più vicini al "valore" della serie:
Le successioni 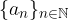 e
e 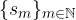 sono strettamente legate tra di loro e non vanno invertite (la seconda si deduce a partire dalla prima!) perciò formano una coppia ordinata:
sono strettamente legate tra di loro e non vanno invertite (la seconda si deduce a partire dalla prima!) perciò formano una coppia ordinata:
Dato che 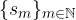 è composta da somme finite che approssimano parzialmente la serie
è composta da somme finite che approssimano parzialmente la serie 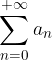 , tale successione è chiamata successione delle somme parziali (o ridotte).
, tale successione è chiamata successione delle somme parziali (o ridotte).
Il termine n-esimo 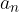 della successione originale che compare a fianco del simbolo di sommatoria
della successione originale che compare a fianco del simbolo di sommatoria  si chiama termine generale della serie.
si chiama termine generale della serie.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Carattere di una serie
Data una serie 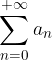 , la successione delle somme parziali (o ridotte)
, la successione delle somme parziali (o ridotte) 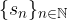 può essere:
può essere:
Convergente: 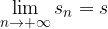 finito allora si dice che la serie converge ed il limite s si chiama somma della serie.
finito allora si dice che la serie converge ed il limite s si chiama somma della serie.
Divergente: 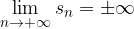 allora si dice che la serie diverge (a più o meno infinito).
allora si dice che la serie diverge (a più o meno infinito).
Indeterminata o Irregolare: la successione delle somme parziali (o ridotte) 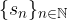 non ha limite (né finito né infinito) allora si dice che la serie è indeterminata.
non ha limite (né finito né infinito) allora si dice che la serie è indeterminata.
Vediamo un esempio di serie divergente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo un esempio di serie indeterminata.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo un esempio di serie convergente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Serie geometrica
Un esempio importante è la serie geometrica associata alla successione geometrica (di ragione q) 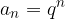 .
.
Riassumiamo qui gli aspetti fondamentali:
La serie geometrica 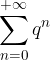 ha tre possibili caratteri:
ha tre possibili caratteri:
Convergente se 
Divergente se  oppure
oppure 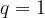
Indeterminata se 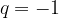
Serie armonica
Un esempio importante è la serie armonica associata alla successione armonica (di esponente p) 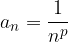 .
.
Riassumiamo qui gli aspetti fondamentali:
La serie armonica 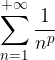 ha due possibili caratteri:
ha due possibili caratteri:
Convergente se 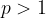 .
.
Divergente se 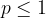 .
.
Criteri di convergenza
Spesso non è possibile scrivere esplicitamente la ridotta n-esima di una serie numerica in funzione di n e calcolarne il limite: per ottenere la somma della serie. In questo capitolo introdurremmo alcuni strumenti elementari per determinare il carattere di una serie numerica senza calcolarne esplicitamente la ridotta n-esima.
Criterio del termine generale
Serie convergenti hanno termine generale infinitesimo.
A prima vista non pare un criterio di convergenza in quanto se sappiamo già che la serie è convergente abbiamo già determinato il suo carattere, infatti di questa proposizione si usa la contro-nominale.
Serie con termine generale non infinitesimo non sono convergenti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Purtroppo non vale il teorema inverso - una serie con termine generale infinitesimo è convergente - come illustra il seguente esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criterio del confronto
Serie a termini positivi definitivamente maggiorate da serie convergenti sono convergenti. Serie definitivamente minorate da serie a termini positivi divergenti sono divergenti.
Vediamo un esempio di serie convergente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo un esempio di serie divergente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Convergenza assoluta
Il criterio precedente è troppo restrittivo in quanto pretende che le serie siano a termini positivi. Introduciamo qui un nuovo tipo di serie numerica ed un risultato particolarmente utile ad esso legato.
Una serie numerica 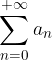 si dice assolutamente convergente se la serie dei moduli dei suoi termini generali
si dice assolutamente convergente se la serie dei moduli dei suoi termini generali 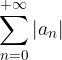 risulta convergente.
risulta convergente.
Le serie assolutamente convergenti godono di un'importante proprietà.
Ogni serie assolutamente convergente è convergente.
Ora possiamo - data una serie numerica arbitraria - vedere se essa è convergente se è assolutamente convergente, applicando alla serie dei moduli dei termini il criterio del confronto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criterio del rapporto
Similmente ai limiti di successioni reali, per determinare il carattere di una serie numerica è sufficiente applicare il criterio del rapporto alla successione dei termini delle serie.
Sia 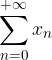 serie numerica a termini mai nulli.
serie numerica a termini mai nulli.
Se esiste q < 1 tale che:
Allora la serie converge assolutamente.
Se invece esiste q > 1 tale che:
Allora la serie diverge assolutamente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criterio della radice
Similmente ai limiti di successioni reali, per determinare il carattere di una serie numerica è sufficiente applicare il criterio della radice alla successione dei termini delle serie.
Sia 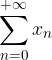 serie numerica.
serie numerica.
Se esiste q < 1 tale che:
Allora la serie converge assolutamente.
Se invece esiste q > 1 tale che:
Allora la serie diverge assolutamente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criterio di Leibniz
I criteri precedenti concludevano l'assoluta convergenza di una serie numerica - proprietà molto forte - e viene spontaneo chiedersi se vi sono serie numeriche che convergono, ma non assolutamente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dall'esempio precedente evinciamo che per una serie a segni alterni la sua convergenza (non assoluta) necessita di condizioni meno restrittive.





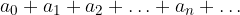
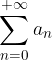
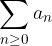
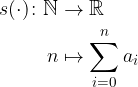
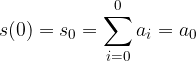
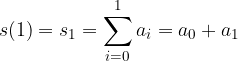
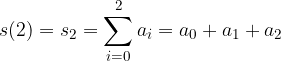
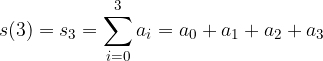
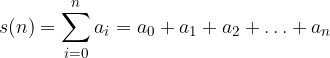
 - la loro somma
- la loro somma 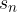 è unica.
è unica.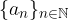 e
e 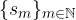 sono strettamente legate tra di loro e non vanno invertite (la seconda si deduce a partire dalla prima!) perciò formano una coppia ordinata:
sono strettamente legate tra di loro e non vanno invertite (la seconda si deduce a partire dalla prima!) perciò formano una coppia ordinata: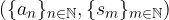
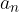 della
della  si chiama termine generale della serie.
si chiama termine generale della serie.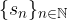 può essere:
può essere: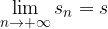 finito allora si dice che la serie converge ed il limite s si chiama somma della serie.
finito allora si dice che la serie converge ed il limite s si chiama somma della serie.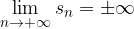 allora si dice che la serie diverge (a più o meno infinito).
allora si dice che la serie diverge (a più o meno infinito).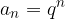 .
.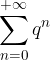 ha tre possibili caratteri:
ha tre possibili caratteri:
 oppure
oppure 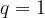
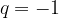
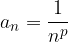 .
.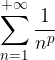 ha due possibili caratteri:
ha due possibili caratteri: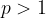 .
.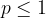 .
.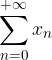 è
è 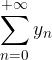 se il termine generale della prima è
se il termine generale della prima è 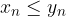 .
.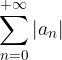 risulta convergente.
risulta convergente.