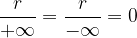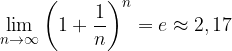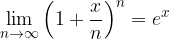Prima del calcolo del limite di una funzione reale di variabile reale, risulta più facile ed intuitivo il calcolo del limite di una successione reale in quanto lo studio è limitato al comportamento della successione per indici arbitrariamente grandi.
Intorno completo
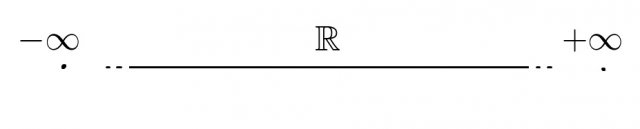
Per poter parlare di limite di una successione reale dobbiamo introdurre un oggetto che ci permetta di poter quantificare il concetto di "vicinanza" tra due punti nella retta reale.
dove il parametro  è strettamente positivo.
è strettamente positivo.
Se immaginiamo tali intorni completi come circonferenze degeneri, gli elementi che li costituiscono hanno nomi propri ereditati dalla geometria:
x è il centro dell' intorno;
 è il raggio dell' intorno;
è il raggio dell' intorno;
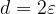 è il diametro o l'ampiezza dell' intorno;
è il diametro o l'ampiezza dell' intorno;
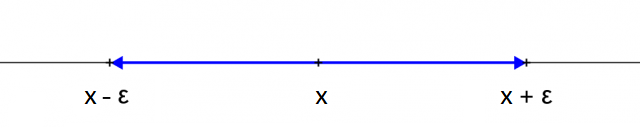
Un intorno completo centrato in x e raggio 
Una proprietà importante è che intersezioni finite di intorni completi sono intorni completi, ovvero:
Scriveremo spesso per semplicità:
per indicare un intorno completo centrato in x di raggio  .
.
Vediamo un esempio per familiarizzare con la nuova terminologia.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La definizione di intorno completo per un numero reale non è sufficiente per spiegare appieno i limiti di successioni reali, in quanto mancherebbe il concetto di "lontananza" in un senso o nell'altro da un punto.
Per fare ciò introduciamo l'insieme dei numeri reali estesi:
L'insieme dei numeri reali estesi è l'insieme dei numeri reali più 2 nuovi elementi 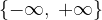
e l'ordine usuale è esteso come segue:
Ora possiamo includere nella definizione di intorno completo anche i nuovi elementi 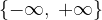
dove il parametro  è strettamente positivo.
è strettamente positivo.
Per questi nuovi tipi di intorno completo, però, essendo intervalli illimitati, non si può parlare di centro o raggio.
Continueremo a indicare per semplicità:
un intorno completo di x e parametro  anche quando x è un numero reale esteso.
anche quando x è un numero reale esteso.
Punti aderenti
Dato un sottoinsieme dei reali estesi, possiamo distinguere i punti della retta reale estesa in due tipologie grazie alla definizione di intorno completo. Vogliamo specificare se un numero reale esteso è "per conto suo" rispetto agli elementi di un insieme oppure se ne è "a stretto contatto".
Tra queste tipologie di punti saranno importanti quelli "per conto loro" appartenenti all'insieme ed i numeri reali estesi (non necessariamente nell'insieme) "a stretto contatto". Sono chiamati di aderenza o aderenti per l'insieme. Vediamo i primi: i punti isolati.
Punti isolati
Dato un sottoinsieme dei reali estesi, i punti nell'insieme si dicono isolati se "guardando attorno" ad esso non vi sono altri elementi dell'insieme:
Sia 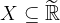 . Un elemento
. Un elemento 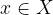 si dice isolato se:
si dice isolato se:
ovvero se esiste un intorno di x non contenente altri elementi di X eccetto lui.

Punto isolato x per un insieme X
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Insiemi discreti
Un insieme dei numeri reali estesi in cui i suoi elementi siano "distanti" tra di loro - ovvero i cui punti sono tutti isolati - è chiamato discreto.
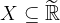 si dice discreto se ha solo punti isolati:
si dice discreto se ha solo punti isolati:
Un esempio molto importante di insieme discreto è il supporto di una successione reale non contenente il proprio limite.
Ciò conferma la nostra intuizione che una successione reale sia un elenco di numeri reali "staccati tra loro" e giustifica la rappresentazione sulla retta reale con singoli punti.
Punti di accumulazione
Dato un sottoinsieme dei reali estesi, un numero reale esteso (non necessariamente nell'insieme) si dice di accumulazione se ha "vicino" molti altri elementi dell'insieme:
Dato un sottoinsieme X di 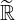 , gli elementi di X che hanno "vicino" molti altri elementi dell'insieme si dicono di accumulazione.
, gli elementi di X che hanno "vicino" molti altri elementi dell'insieme si dicono di accumulazione.
Ci sembra ragionevole proporre tale definizione:
Sia 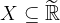 . Un elemento
. Un elemento 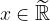 si dice di accumulazione se:
si dice di accumulazione se:
ovvero se ogni intorno di x ha almeno un altro elemento diverso di X.
Possiamo riscrivere la precedente definizione senza coinvolgere y:
Sia  . Un elemento
. Un elemento  si dice di accumulazione se:
si dice di accumulazione se:
ovvero se ogni intorno di x ha almeno un altro elemento diverso di X.
Punto di accumulazione x per un insieme X
Osserviamo che se x è un numero reale non appartenente all'insieme X, allora la sottrazione diventa X - {x} = X.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Insiemi Chiusi
Un insieme dei numeri reali estesi in cui punti "vicini" all'insieme sono contenuti - ovvero contiene tutti i suoi punti di accumulazione - è chiamato chiuso.
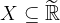 si dice chiuso se contiene tutti i suoi punti di accumulazione:
si dice chiuso se contiene tutti i suoi punti di accumulazione:
ovvero se ogni numero reale esteso per cui ogni suo intorno interseca l'insieme in un punto distinto da lui appartiene all'insieme.
Ciò conferma la nostra intuizione che un intervallo chiuso sia un insieme di numeri reali "vicini tra loro" e che tutti i numeri reali "vicini" all'insieme appartengono all'insieme e giustifica la rappresentazione sulla retta reale con un segmento con estremi inclusi.
Successioni definitivamente
Nel capitolo successioni reali abbiamo introdotto molte proprietà (monotonia, definitezza, ecc.), ma tali proprietà erano molto restrittive in quanto venivano coinvolti tutti i termini.
Data una successione che gode di qualche proprietà interessante, vi sono un sacco di successioni che le "assomigliano", ma che non godono più di tale proprietà.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nell'esempio precedente abbiamo visto come sia sufficiente modificare un numero finito di termini di una successione reale che gode di alcune proprietà per ottenerne un'altra molto simile, ma priva di esse.
Tuttavia non tutto è perduto: è sufficiente escludere i "pochi" termini che non soddisfano la proprietà.
Per ricordarci di tale operazione aggiungiamo la parola definitivamente prima di una proprietà che equivale a eccetto un numero finito di termini.
Sia 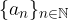 una successione reale e
una successione reale e 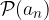 una proprietà delle successioni reali (monotona, definita, ecc.).
una proprietà delle successioni reali (monotona, definita, ecc.).
La successione reale gode definitivamente di tale proprietà se da un certo indice in poi i termini soddisfano tale proprietà - ovvero se tale proprietà non è soddisfatta per un numero finito di termini:
Limite di una successione reale
Prima di enunciare la definizione che può risultare ostica e contro-intuitiva, vediamo con un esempio la ragionevolezza di essa.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dall'esempio precedente non siamo ancora giunti alla definizione di limite di una successione reale, in quanto vi sono successioni che hanno termini sempre più grandi positivi o negativi, ma è sufficiente passare all'insieme dei reali estesi per ovviare al problema.
Sia 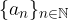 una successione reale. Essa ammette limite
una successione reale. Essa ammette limite 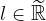 se è verificata la proposizione:
se è verificata la proposizione:
In tal caso scriviamo semplicemente
Alla luce della terminologia precedente (punti isolati, di accumulazione, definitivamente) semplifichiamo la definizione di limite:
Sia 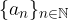 una successione reale. Essa ammette limite
una successione reale. Essa ammette limite 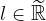 solo se il suo supporto:
solo se il suo supporto:
Ha definitivamente come (unico) punto di aderenza l.
L'aggettivo unico sarà oggetto di un teorema molto importante che illustreremo più avanti.
Successioni reali convergenti
Nel caso particolare in cui una successione reale 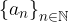 ammetta per limite un numero reale l, la successione si dice convergente (o che converge a l). In tale caso semplifichiamo ulteriormente la notazione data di limite:
ammetta per limite un numero reale l, la successione si dice convergente (o che converge a l). In tale caso semplifichiamo ulteriormente la notazione data di limite:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se il limite di una successione è 0 allora la successione è detta anche infinitesima.
Successioni reali divergenti
In tale caso semplifichiamo ulteriormente la notazione data di limite:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali indeterminate
Un caso che si può presentare per una successione reale è che essa non ammetta limite: in tal caso la successione è chiamata indeterminata.
Quando una successione 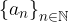 non ammetterà limite scriveremo:
non ammetterà limite scriveremo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Teoremi sui limiti
Vi sono alcuni risultati importanti riguardanti la nozione di limite. Prima fra tutte se esso sia unico, poi se possiamo dedurre qualche proprietà della successione conoscendo il limite ed infine di determinare limiti di successioni "complicate" da altre più "semplici". Partiamo con l'unicità.
Unicità del limite
Abbiamo già accennato nella definizione di limite che esso - se esiste - è unico.
Vedremo più avanti un'immediata conseguenza di tale teorema riguardante limiti di sotto-successioni.
Permanenza del segno
Se sappiamo che una successione reale 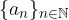 ammette limite l e tale limite non è nullo (l > 0 o l < 0) allora possiamo dedurre che la successione è definitivamente strettamente positiva (negativa).
ammette limite l e tale limite non è nullo (l > 0 o l < 0) allora possiamo dedurre che la successione è definitivamente strettamente positiva (negativa).
Se per una successione reale 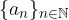 abbiamo:
abbiamo:
allora essa è definitivamente strettamente positiva:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il teorema si può generalizzare con due successioni reali che ammettono limiti distinti.
Se per due successioni reali 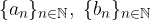 ammettono limiti distinti (ad esempio il primo minore del secondo):
ammettono limiti distinti (ad esempio il primo minore del secondo):
allora anche i termini della I successione sono definitivamente minori dei termini della II:
Teorema del confronto
Questo teorema è il contro-nominale del precedente: se date due successioni reali una minore o uguale dell'altra definitivamente allora anche i limiti sono uno minore o uguale dell'altro - se esistono.
Siano 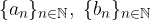 due successioni reali una minore o uguale dell'altra definitivamente:
due successioni reali una minore o uguale dell'altra definitivamente:
allora anche i limiti - se esistono - hanno il medesimo ordine:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Teorema dei carabinieri
Questo teorema è molto importante perché è diretta conseguenza dei precedenti e permette di dedurre il limite di una successione compresa definitivamente tra altre due di cui sappiamo che hanno il medesimo limite, in quanto coincide con esso.
Siano 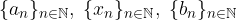 tre successioni reali tali che la II sia definitivamente compresa fra le altre due:
tre successioni reali tali che la II sia definitivamente compresa fra le altre due:
Se la I e la III successione ammettono medesimo limite l allora anche la rimante ammette limite e coincide con esso:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il teorema funziona anche per successioni divergenti, ma è sufficiente una sola successione delle due nell'enunciato iniziale. In effetti è un caso particolare del teorema del confronto:
Siano 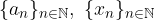 due successioni reali tali che siano definitivamente una minore o uguale all'altra:
due successioni reali tali che siano definitivamente una minore o uguale all'altra:
Criteri di convergenza
Non è sempre possibile calcolare semplicemente il limite di una successione reale. In questo capitolo introdurremmo alcuni strumenti elementari per determinarne il carattere (convergente, divergente, indeterminata) semplificando la successione da studiare.
I vari criteri si basano su un fatto fondamentale riguardante successioni monotone.
Successioni reali monotone hanno sempre limite. In particolare:
successioni crescenti hanno per limite l'estremo superiore (minimo dei maggioranti) del supporto ;
successioni decrescenti hanno per limite l'estremo inferiore (massimo dei maggioranti) del supporto;
L'enunciato può essere esteso a successioni reali definitivamente monotone:
Successioni reali definitivamente monotone hanno sempre limite.
Limiti di sotto-successioni
Data una successione reali, possiamo estrarre da essa molte sotto-successioni. Se quella data ammette limite è ragionevole supporre che anche tutte le sue sotto-successioni ammettano il medesimo limite.
Se 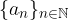 è una successione reale che ammette limite l, allora ogni sotto-successione estratta ha limite l:
è una successione reale che ammette limite l, allora ogni sotto-successione estratta ha limite l:
A prima vista non pare un criterio di convergenza in quanto, se sappiamo il limite della successione, allora abbiamo già determinato il suo carattere, infatti di questa proposizione si usa la contro-nominale.
Successioni reali con sotto-successioni estratte convergenti (o divergenti) a limiti differenti non hanno limite:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Criterio del rapporto
Un metodo utile per determinare rapidamente se una successione reale strettamente positiva è infinitesima o meno è quello di studiare come si comporta il rapporto tra un termine ed il suo precedente.
Sia 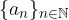 è una successione reale strettamente positiva. A seconda che il rapporto tra un termine ed il suo precedente:
è una successione reale strettamente positiva. A seconda che il rapporto tra un termine ed il suo precedente:
Converga ad un numero l maggiore o minore di 1 allora la successione data diverge a 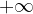 o è infinitesima.
o è infinitesima.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in cui il rapporto tenda a 1, in quanto in tale situazione non è possibile concludere.
Consideriamo le successioni reali:
Conosciamo già i loro limiti:
Per il criterio del rapporto abbiamo:
Otteniamo che entrambi i rapporti hanno il medesimo comportamento, ma le successioni di partenza hanno carattere completamente differente (una convergente, l'altra divergente!).
Il medesimo criterio può essere applicato alle serie numeriche per studiarne la convergenza.
Criterio della radice
Un metodo utile per determinare rapidamente se una successione reale positiva è infinitesima o meno è quello di studiare come si comporta la radice n-esima del termine n-esimo.
Sia 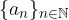 è una successione reale positiva. A seconda che la radice n-esima del termine n-esimo:
è una successione reale positiva. A seconda che la radice n-esima del termine n-esimo:
Converga ad un numero l maggiore o minore di 1 allora la successione data diverge a 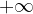 o è infinitesima.
o è infinitesima.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in la radice tenda a 1, in quanto in tale situazione non è possibile concludere.
Consideriamo le successioni reali:
La prima converge al numero di Nepero, ma la seconda a 1:
Per il criterio del rapporto abbiamo:
Otteniamo che entrambi le radici hanno il medesimo comportamento, ma le successioni di partenza sono convergenti a due limiti distinti non nulli.
Il medesimo criterio può essere applicato alle serie numeriche per studiarne la convergenza.
Operazioni con i limiti
Vedremo nei prossimi capitoli che con la nozione di limite potremmo estendere alcune operazioni tra numeri reali ai numeri reali estesi. Cominciamo dalla somma.
Somma di limiti
Date due successioni reali, se esse hanno un particolare andamento allora possiamo dedurre l'andamento della successione somma.
Date due successioni reali 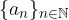 e
e 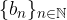 tali che:
tali che:
la prima diverge a 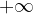 (a
(a 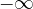 ) e la seconda è definitivamente limitata a sinistra (a destra);
) e la seconda è definitivamente limitata a sinistra (a destra);
allora la successione somma 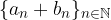 ammette limite ed in particolare:
ammette limite ed in particolare:
converge alla somma dei limiti;
diverge a 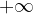 (a
(a 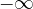 );
);
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in cui le successioni divergono a due limiti diversi, in quanto in tale situazione non è possibile concludere (forma indeterminata  ).
).
Consideriamo le seguenti successioni reali:
Conosciamo il limite per ognuna di loro:
Possiamo scrivere ognuna come somma non banale di due successioni reali.
Otteniamo che tutti gli addendi hanno il medesimo comportamento, ma le successioni di partenza hanno carattere completamente differente (una convergente, e due divergenti a limiti diversi!).
Con il risultato precedente possiamo estendere parzialmente la somma tra numeri reali a quelli estesi:
Se 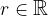 allora valgono le seguenti uguaglianze:
allora valgono le seguenti uguaglianze:
Prodotto di limiti
Date due successioni reali, se esse hanno un particolare andamento allora possiamo dedurre l'andamento della successione prodotto.
Date due successioni reali 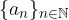 e
e 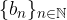 tali che:
tali che:
allora la successione prodotto 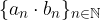 ammette limite ed in particolare:
ammette limite ed in particolare:
converge al prodotto dei limiti;
diverge a 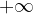 (a
(a 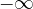 );
);
diverge a 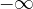 (a
(a 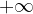 );
);
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in cui una successione è infinitesima e l'altra diverge, in quanto in tale situazione non è possibile concludere (forma indeterminata 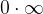 ).
).
Consideriamo le seguenti successioni reali:
Conosciamo il limite per ognuna di loro:
Possiamo scrivere ognuna come prodotto non banale di due successioni reali.
Otteniamo che tutti i fattori hanno il medesimo comportamento, ma le successioni di partenza hanno carattere completamente differente (una convergente, e due divergenti a limiti diversi!).
Con il risultato precedente possiamo estendere parzialmente il prodotto tra numeri reali a quelli estesi:
Se 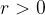 allora valgono le seguenti uguaglianze:
allora valgono le seguenti uguaglianze:
Reciproci di limiti
Date una successione reale, se essa ha un particolare andamento allora possiamo dedurre l'andamento della successione reciproco.
Data una successione reale 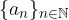 tale che:
tale che:
sia convergente non infinitesima;
diverge a 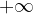 (a
(a 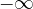 );
);
infinitesima e definitivamente strettamente positiva (negativa);
allora la successione reciproco 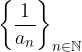 ammette limite ed in particolare:
ammette limite ed in particolare:
converge al reciproco del limite;
diverge a 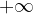 (a
(a 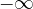 );
);
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in cui una successione è infinitesima ma non è definitivamente strettamente positiva o negativa, in quanto in tale situazione non è possibile concludere.
Consideriamo la seguente successione reale:
Si tratta di una successione infinitesima:
Essendo una successione a segno alterno non è definitivamente strettamente positiva né negativa.
La successione reciproco:
Non ha limite in quanto la sotto-successione dei termini pari e quella dei termini dispari hanno limiti diversi:
Con il risultato precedente possiamo estendere parzialmente il reciproco tra numeri reali a quelli estesi:
Valgono le seguenti uguaglianze:
Prodotto di limiti
Date due successioni reali, se esse hanno un particolare andamento allora possiamo dedurre l'andamento della successione rapporto.
Date due successioni reali 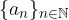 e
e 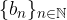 tali che:
tali che:
siano convergenti e la seconda non infinitesima;
definitivamente strettamente concordi (discordi), la prima non infinitesima e la seconda infinitesima;
la prima è limitata e la seconda diverge a 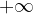 (a
(a 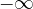 );
);
allora la successione rapporto 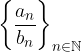 ammette limite ed in particolare:
ammette limite ed in particolare:
converge al rapporto dei limiti;
diverge a 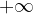 (a
(a 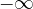 );
);
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Non abbiamo parlato del caso in cui le due successioni sono infinitesime o entrambe divergenti, in quanto in tali situazione non è possibile concludere (forme indeterminate  e
e 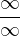 ).
).
Consideriamo le seguenti successioni reali:
Conosciamo il limite per ognuna di loro:
Possiamo scrivere ognuna come rapporto non banale di due successioni reali.
Otteniamo che tutti i fattori hanno il medesimo comportamento, ma le successioni di partenza hanno carattere completamente differente (una convergente, e due divergenti a limiti diversi!).
Con il risultato precedente possiamo estendere parzialmente il rapporto tra numeri reali a quelli estesi:
Se 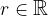 allora valgono le seguenti uguaglianze:
allora valgono le seguenti uguaglianze:
Numero di Nepero o Eulero
Una delle costanti in matematica più importanti è data dal limite della seguente successione reale convergente:
Tale numero reale viene chiamato in 2 modi:
in ambito internazionale è il Numero di Eulero in onore del matematico e fisico svizzero Leonhard Euler;
in Italia è il Numero di Nepero in onore del matematico, fisico e astronomo scozzese John Napier;
La successione precedente si può generalizzare come segue.
Dove x è un qualunque numero reale.





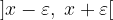
 è strettamente positivo.
è strettamente positivo. con un suo
con un suo 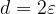 è il diametro o l'ampiezza dell' intorno;
è il diametro o l'ampiezza dell' intorno;
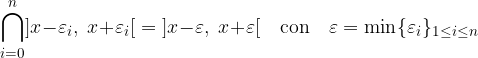
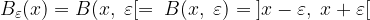
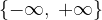
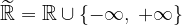
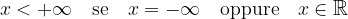
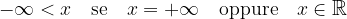
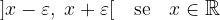
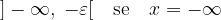
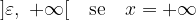
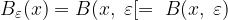
 . Un elemento
. Un elemento 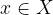 si dice isolato se:
si dice isolato se: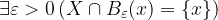

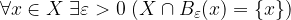
 , gli elementi di X che hanno "vicino" molti altri elementi dell'insieme si dicono di accumulazione.
, gli elementi di X che hanno "vicino" molti altri elementi dell'insieme si dicono di accumulazione.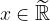 si dice di accumulazione se:
si dice di accumulazione se: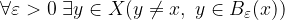
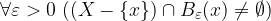

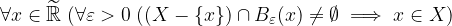
 una successione reale e
una successione reale e  una proprietà delle successioni reali (monotona, definita, ecc.).
una proprietà delle successioni reali (monotona, definita, ecc.).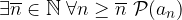
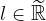 se è verificata la proposizione:
se è verificata la proposizione: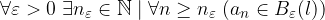
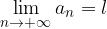
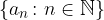
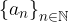 ammetta per limite un numero reale l, la successione si dice convergente (o che converge a l). In tale caso semplifichiamo ulteriormente la notazione data di limite:
ammetta per limite un numero reale l, la successione si dice convergente (o che converge a l). In tale caso semplifichiamo ulteriormente la notazione data di limite: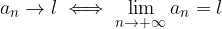
 la successione si dice divergente (o che diverge a
la successione si dice divergente (o che diverge a 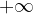 oppure
oppure 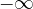 ).
).
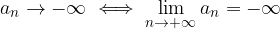
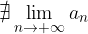
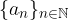 è un successione reale che ha per limiti
è un successione reale che ha per limiti 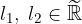 , allora
, allora 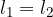 .
.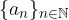 ammette limite l e tale limite non è nullo (l > 0 o l < 0) allora possiamo dedurre che la successione è definitivamente strettamente positiva (negativa).
ammette limite l e tale limite non è nullo (l > 0 o l < 0) allora possiamo dedurre che la successione è definitivamente strettamente positiva (negativa).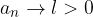
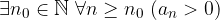
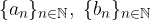 ammettono limiti distinti (ad esempio il primo minore del secondo):
ammettono limiti distinti (ad esempio il primo minore del secondo):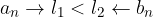
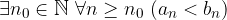
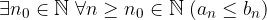
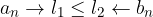
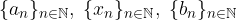 tre successioni reali tali che la II sia definitivamente compresa fra le altre due:
tre successioni reali tali che la II sia definitivamente compresa fra le altre due: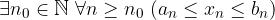
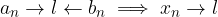
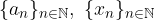 due successioni reali tali che siano definitivamente una minore o uguale all'altra:
due successioni reali tali che siano definitivamente una minore o uguale all'altra: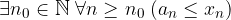
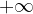 allora anche la seconda diverge a
allora anche la seconda diverge a 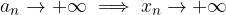
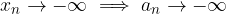
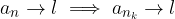
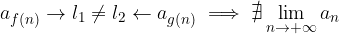
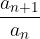
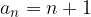
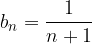
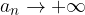
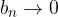
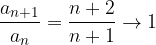
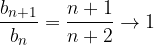
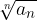
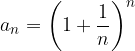
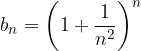
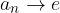
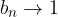
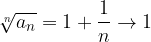
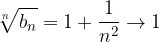
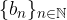 tali che:
tali che: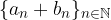 ammette limite ed in particolare:
ammette limite ed in particolare: ).
).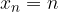
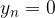
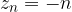
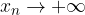
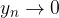
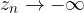
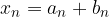 con
con 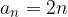 e
e 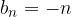 , ma
, ma 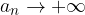 e
e 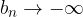
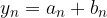 con
con 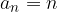 e
e 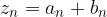 con
con 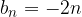 , ma
, ma 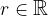 allora valgono le seguenti uguaglianze:
allora valgono le seguenti uguaglianze: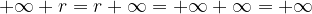
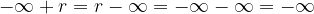
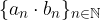 ammette limite ed in particolare:
ammette limite ed in particolare: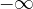 (a
(a 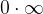 ).
).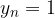
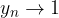
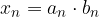 con
con 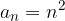 e
e 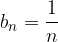 , ma
, ma 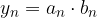 con
con 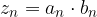 con
con 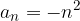 e
e 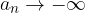 e
e 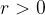 allora valgono le seguenti uguaglianze:
allora valgono le seguenti uguaglianze: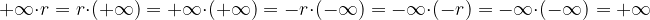
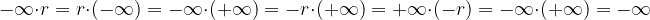
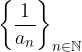 ammette limite ed in particolare:
ammette limite ed in particolare: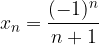
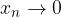
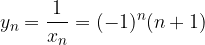
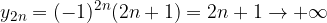
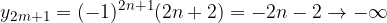
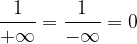
 ammette limite ed in particolare:
ammette limite ed in particolare: e
e  ).
).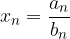 con
con 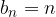 , ma
, ma 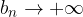
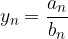 con
con 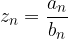 con
con