In questo capitolo prenderemo in considerazione le seguenti funzioni trigonometriche:
Consideriamo i seguenti tipi di limiti:
limite in un determinato punto (ad esempio 
)
limite all'infinito.
Sappiamo che il limite di una funzione nel punto è:
Considerando i grafici delle funzioni seno e coseno, sappiamo che si tratta di funzioni che sono continue in tutta l'area di calcolo, pertanto per i loro limiti valgono:
Limite della funzione seno in un punto:
Limite della funzione coseno in un punto:
Particolarmente interessante è il limite seguente:
In questo caso, per x=0, avremmo:
La funzione non è dunque definita nel punto x=0, tuttavia il limite della funzione per x che tende a zero è:
Dimostriamo quanto detto aiutandoci con la seguente rappresentazione grafica:
Nel cerchio unitario, consideriamo l'arco di lunghezza x che si oppone all'angolo x (in radianti). Consideriamo ora la disuguaglianza:
Tale disuguaglianza sussiste in quanto, come si vede dalla figura, l'arco x è proprio compreso tra la funzione 
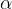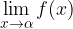
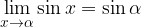
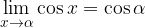
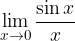
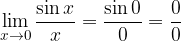
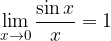
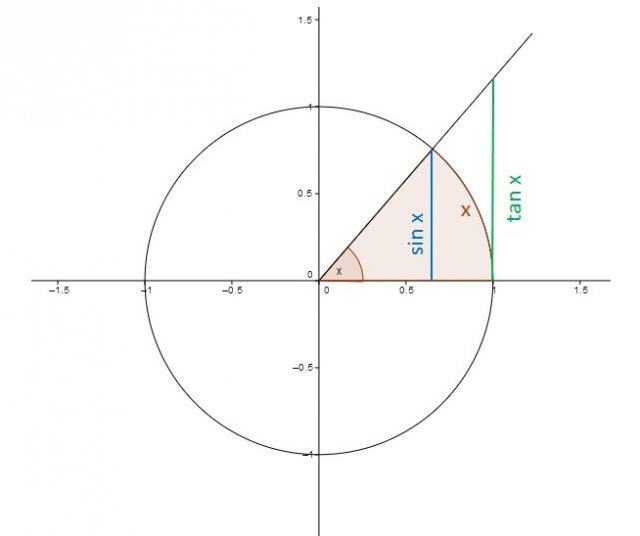
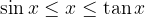
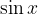e la funzione 
.
Abbiamo dunque dimostrato il valore di questo limite fondamentale che può essere utile alla risoluzione di diversi problemi:
Il limite della funzione
per x che tende a 0 è uguale a 1
ovvero:
Sappiamo che un limite all'infinito è del tipo:
Sappiamo anche che le funzioni seno e coseno oscillano tra -1 e 1, per cui possiamo affermare quanto segue:
Non possiamo parlare di limiti all'infinito per le funzioni seno e coseno in quanto oscillano tra i valori -1 e 1, ovvero i limiti:
e
non esistono.
Considerando i grafici delle funzioni tangente e cotangente, possiamo affermare quanto segue:
Tangente e cotangente sono funzioni continue a tratti, soggette alle seguenti condizioni:
Il limite
non esiste, in quanto per x che tende a 
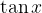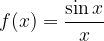
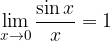
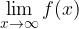
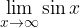
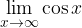
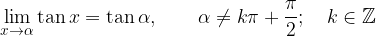
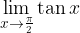
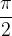da sinistra la funzione tende all'infinito, mentre quando x tende a 
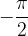da destra la funzione tende a meno infinito. Lo stesso accade per la funzione cotangente tra i valori 
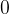e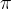 
.
