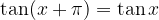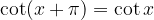Si prenda un triangolo rettangolo:
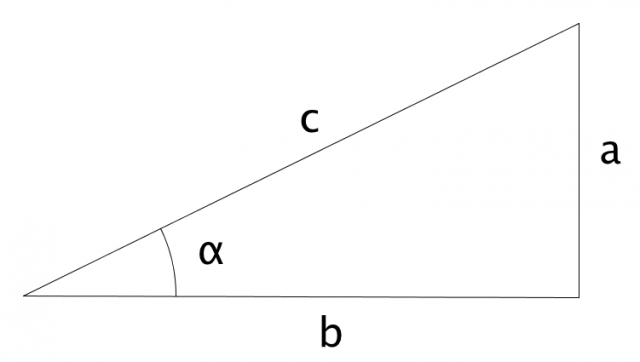
Triangolo rettangolo; il lato b è adiacente all'angolo α, il lato a è opposto
all'angolo α
Le funzioni tangente e cotangente in un triangolo retto mettono in relazione l'angolo acuto ed i cateti del triangolo:
La funzione tangente dell'angolo 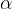 è definita come il rapporto tra il cateto opposto (a) e il cateto adiacente (b):
è definita come il rapporto tra il cateto opposto (a) e il cateto adiacente (b):
La funzione cotangente dell'angolo 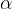 è definita come il rapporto tra il cateto adiacente (b) e il cateto opposto (a):
è definita come il rapporto tra il cateto adiacente (b) e il cateto opposto (a):
Grafico delle funzioni tangente e cotangente
Tracciamo le funzioni tangente e cotangente su un cerchio unitario:
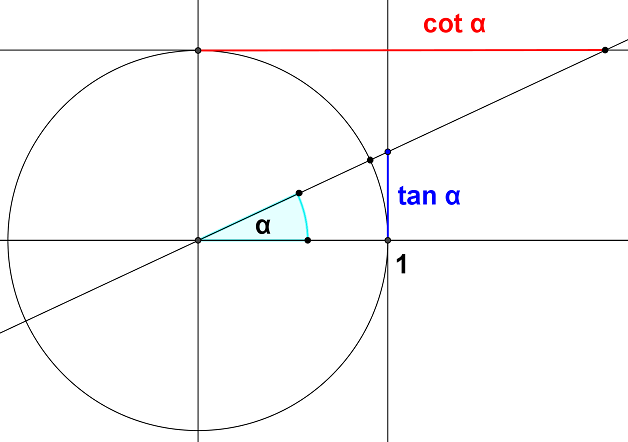
Funzioni tangente e cotangente su un cerchio unitario
I valori di tangente e cotangente sono meno facili da leggere con il cerchio unitario, per cui nel tracciamento ci aiuteremo con i valori di seno e coseno che già conosciamo (allargheremo la tabella e calcoleremo i valori da 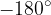 a
a 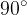 ), rendendo più facile il tracciamento della tangente e della cotangente.
), rendendo più facile il tracciamento della tangente e della cotangente.
Per il calcolo della tangente e cotangente utilizzeremo le formule:
Il valore dell'angolo α si misura in radianti. Questo significa che il valore dell'angolo giro è 3.14159... e non 180°.
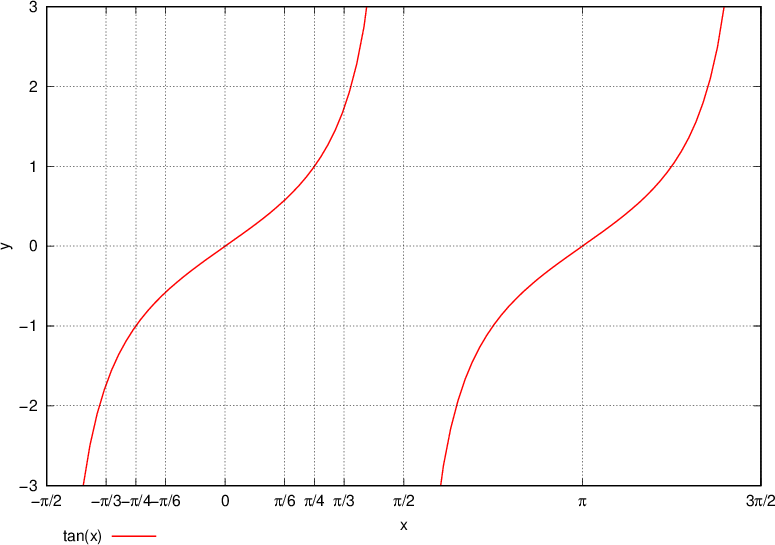
Tracciamo la funzione tangente. Sull'asse x riportiamo il valore dell'angolo α, sull'asse y il valore della tangente:
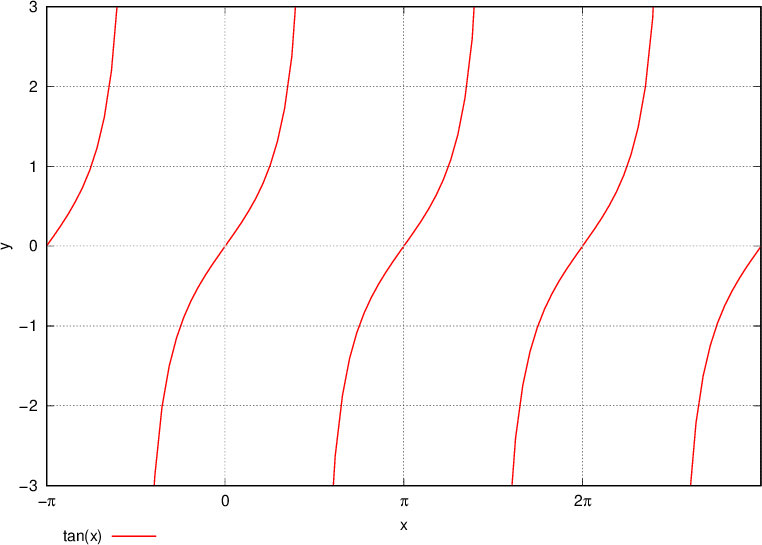
Grafico della funzione tangente di x
Nel tracciare la funzione tangente riportiamo l'angolo α sull'asse x.
Ricaviamo i valori dalla tabella e li confrontiamo col grafico. I valori devono corrispondere:
Abbiamo completato un cerchio intero; se ne facciamo un altro gli stessi passi si ripeteranno. La funzione si ripete visibilmente ad intervalli di 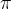 .
.
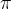 è pertanto il periodo della funzione.
è pertanto il periodo della funzione.
La funzione tangente è periodica con periodo 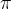 . Sul grafico è facile rilevare la periodicità ed il ripetersi della funzione.
. Sul grafico è facile rilevare la periodicità ed il ripetersi della funzione.
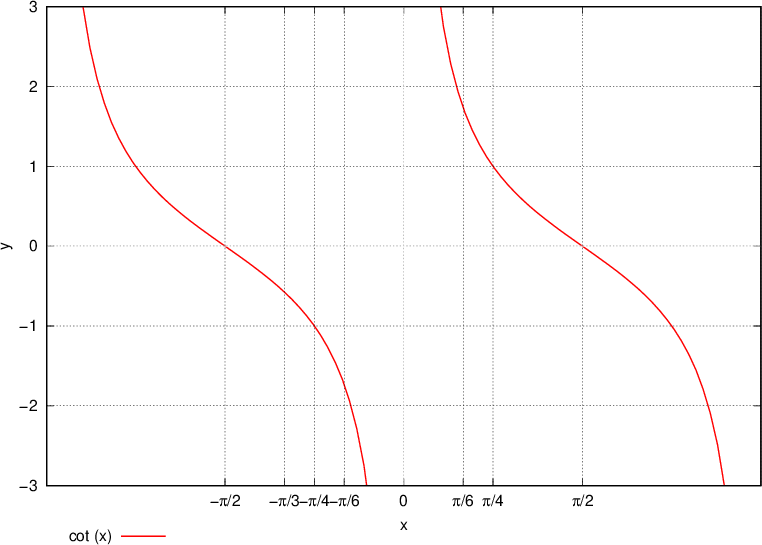
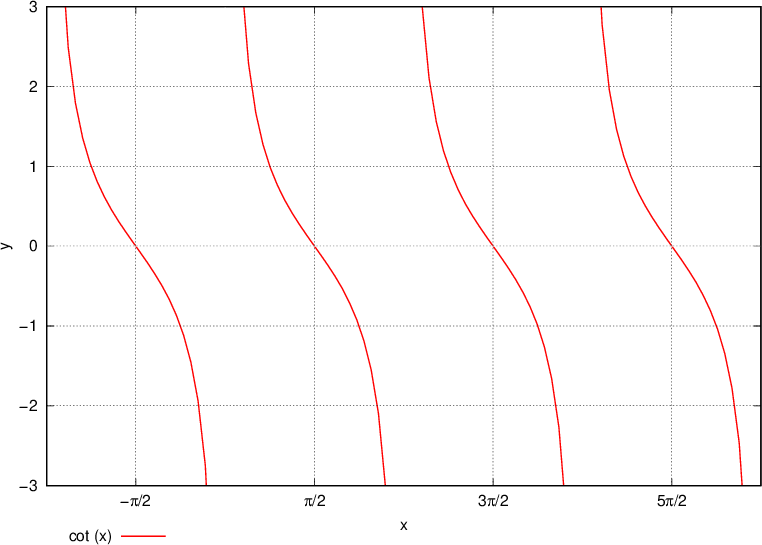
Grafico della funzione cotangente di x
Nel tracciare la funzione cotangente riportiamo l'angolo α sull'asse x.
Analogo procedimento si ripete nel caso della cotangente - leggiamo i valori dalla tabella confrontandoli col grafico - i valori devono corrispondere.
Abbiamo portato a termine un cerchio completo; se ne facciamo un altro gli stessi passi si ripeteranno. La funzione visibilmente si ripete ogni 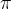 .
.
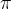 è pertanto il periodo della funzione.
è pertanto il periodo della funzione.
La funzione cotangente è periodica con periodo 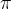 . Sul grafico è facile visualizzare la periodicità ed il ripetersi della funzione.
. Sul grafico è facile visualizzare la periodicità ed il ripetersi della funzione.
Proprietà delle funzioni tangente e cotangente
Le proprietà delle due funzioni sono facilmente ricavabili dal grafico. Ira descriveremo le proprietà che abbiamo rilevato dal grafico anche in termini matematici.
Dominio e valori delle funzioni tan x e cot x
Al dominio di una funzione appartengono tutti gli x che possiamo tracciare sul grafico e per i quali esiste la funzione.
Tangente e cotangente sono definiti come frazioni. Sappiamo che una frazione non può esistere (non è definita) se il denominatore è uguale a 0, per cui elimineremo dal dominio tutti quei valori di funzione che presentano un valore del denominatore di 0. Chiameremo questi valori poli o asintoti verticali.
I valori della funzione sono tutti gli y presenti nel grafico.
Dominio e valori della funzione tan x
La funzione tangente è definita come
La tangente presenta i poli esattamente quando è 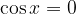 (zeri del coseno), e questo si ha ogni:
(zeri del coseno), e questo si ha ogni:
Dominio della funzione tangente è tutto l'asse reale x senza  , ovvero:
, ovvero:
Dal grafico della funzione tangente e dalla tabella possiamo osservare che l'arco dei valori della funzione è 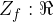 .
.
Valori della funzione tangente:
Dominio e valori della funzione cot x
La funzione cotangente è definita come
La cotangente presenta i poli esattamente quando è 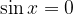 (zeri del seno), e questo si ha ogni
(zeri del seno), e questo si ha ogni
Il dominio della funzione cotangente è tutto l'asse reale x senza 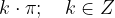 .
.
Al dominio appartengono tutti gli y presenti nel grafico. Dal grafico della funzione cotangente e dalla tabella possiamo osservare che l'arco dei valori della funzione è 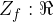 .
.
Valori della funzione cotangente:
Zeri delle funzioni tan x e cot x
Gli zeri della funzione sono quei punti dove la funzione interseca l'asse x.
Zeri di tan x
Gli zeri della tangente si trovano ad ogni multiplo di 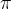 , ovvero la funzione tangente ha valore zero per gli angoli:
, ovvero la funzione tangente ha valore zero per gli angoli:
Ricaviamo gli zeri della tangente con l'enunciato:
La soluzione dell'enunciato è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Zeri di cot x
Gli zeri della cotangente si trovano ad ogni multiplo di 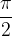 (zeri del coseno).
(zeri del coseno).
Ricaviamo gli zeri della cotangente con l'enunciato:
La soluzione dell'enunciato è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Poli delle funzioni tangente e cotangente
Poli di tan x
I poli della tangente si trovano ad ogni multiplo di 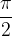 (zeri del coseno), ovvero la tangente per questi valori non esiste (non è definita).
(zeri del coseno), ovvero la tangente per questi valori non esiste (non è definita).
Ricaviamo i poli della tangente con l'enunciato:
La soluzione dell'enunciato è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Poli di cot x
I poli della cotangente si trovano ad ogni multiplo di 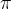 (zeri del seno):
(zeri del seno):
Ricaviamo i poli della cotangente con l'enunciato:
La soluzione dell'enunciato è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Parità e disparità delle funzioni tangente e cotangente
La funzione è pari se è simmetrica rispetto all'origine delle coordinate, ovvero:
La funzione è dispari se simmetrica rispetto all'asse y:
Disparità della funzione tan x
Per la funzione tangente vale:
come possiamo verificare dal grafico (la funzione è simmetrica rispetto all'origine delle coordinate). La funzione è evidentemente dispari.
Disparità di cot x
Per la funzione cotangente vale:
come possiamo verificare dal grafico (la funzione è simmetrica rispetto all'origine delle coordinate). La funzione cotangente è evidentemente dispari.
L'andamento delle funzioni tan x in cot x
Crescita di tan x[uredi]
La crescita della tangente è facilmente rilevabile dal grafico. La funzione cresce per tutto il 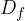 .
.
Decrescita di cot x
Anche la decrescita della cotangente è facile da verificare. La cotangente decresce per tutto il 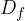 .
.
Periodicità di tan x e cot x
Le funzioni tangente e cotangente sono periodiche con periodo 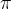 . Possiamo facilmente vedere questa periodicità/ripetizione nel grafico.
. Possiamo facilmente vedere questa periodicità/ripetizione nel grafico.
La funzione tangente è periodica con periodo 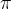 .
.
La funzione cotangente è periodica con periodo 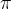 .
.
Continuità delle funzioni tangente e cotangente
Le funzioni tangente e cotangente sono discontinue. Nel grafico lo vediamo nei punti in cui si "interrompono" in corrispondenza dei poli.






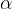 è definita come il rapporto tra il cateto opposto (a) e il cateto adiacente (b):
è definita come il rapporto tra il cateto opposto (a) e il cateto adiacente (b):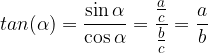
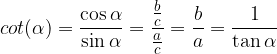

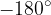 a
a 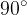 ), rendendo più facile il tracciamento della tangente e della cotangente.
), rendendo più facile il tracciamento della tangente e della cotangente.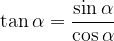
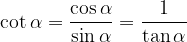
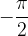 ricavandone il valore
ricavandone il valore 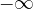 .
.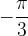 , il valore ricavato è
, il valore ricavato è 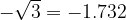 .
.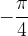 , leggendovi il valore della tangente
, leggendovi il valore della tangente 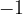 .
.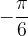 leggiamo il valore
leggiamo il valore 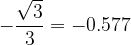 .
.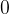 leggiamo il valore di tangente
leggiamo il valore di tangente 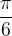 leggiamo dalla tabella il valore della funzione tangente, che è uguale a
leggiamo dalla tabella il valore della funzione tangente, che è uguale a 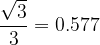 .
.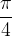 la tangente raggiunge il valore di
la tangente raggiunge il valore di 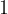 .
.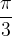 rileviamo il valore di tangente
rileviamo il valore di tangente 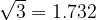 .
.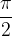 , rileviamo il valore di tangente
, rileviamo il valore di tangente  , da qui in avanti i valori si ripetono e possiamo concludere che la tangente si ripete ogni
, da qui in avanti i valori si ripetono e possiamo concludere che la tangente si ripete ogni 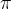 .
.
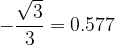 .
.
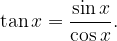
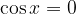 (zeri del coseno), e questo si ha ogni:
(zeri del coseno), e questo si ha ogni: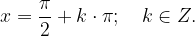
 , ovvero:
, ovvero: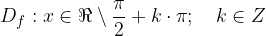
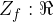 .
.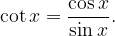
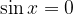 (zeri del seno), e questo si ha ogni
(zeri del seno), e questo si ha ogni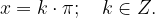
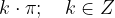 .
.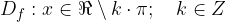
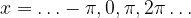
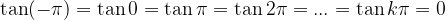
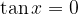
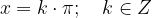
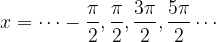
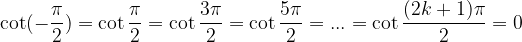
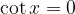
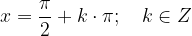
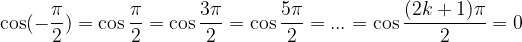
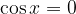
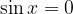
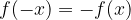
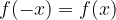
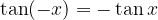
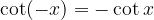
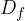 .
.