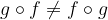Una funzione f è un tipo particolare di relazione che associa ad ogni elemento di un insieme di partenza A, detto dominio, uno e un solo elemento appartenente a un insieme di arrivo B detto codominio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Definizione di funzione
Una funzione in simboli si scrive:
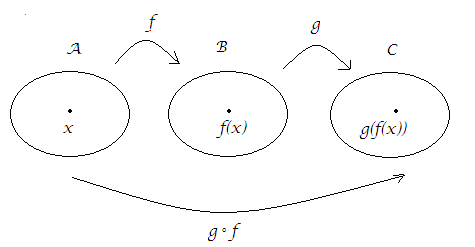
e si legge: f funzione da A a B.
Se chiamiamo x un elemento di A e y un elemento di B, possiamo anche indicare la corrispondenza fra i due valori in questo modo:
Generalmente indichiamo una funzione in questo modo:
Il valore di y dipende da quello attribuito a x, pertanto:
x si chiama variabile indipendente;
y si chiama variabile dipendente;
La y viene anche chiamata immagine di x tramite la funzione f.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Questa non è una funzione! Consideriamo due insiemi:
A l'insieme di tutte le persone;
B l'insieme di tutti gli animali domestici;
Consideriamo una funzione f il cui significato è:
x ha come animale domestico y
La nostra f non è una funzione: possono esistere persone che non hanno animali domestici, oppure possono esistere persone che hanno più di un animale domestico.
Funzioni reali di variabile reale
In seguito parleremo prevalentemente di funzioni numeriche, ossia funzioni che hanno per dominio A e per codominio B, degli insiemi di numeri.
Se A e B sono insiemi che corrispondo all'insieme dei reali, ovvero:
si parla di funzioni reali di variabile reale.
Grafico di una funzione
Il grafico è il modo per rappresentare una funzione e capire visivamente come agisce.
Il grafico di una funzione f è definito come l'insieme dei punti del piano cartesiano di coordinate (x; y), in cui:
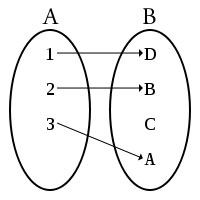
la x appartiene al dominio di f;
y è l'immagine di x mediante la funzione f; e vale y= f(x);
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Zeri di una funzione
Si dice zero di una funzione un valore di x che annulla la funzione, ovvero tale per cui f(x)=0.
Lo zero di una funzione è un valore della variabile x per cui:
Una funzione può avere più zeri. Essi si trovano a partire dall'espressione analitica della funzione, risolvendo l'equazione f(x)=0;
Oppure si possono leggere direttamente dal grafico: sono le ascisse dei punti di intersezione del grafico della funzione con l'asse x. Ad esempio con le funzioni possiamo risolvere graficamente le equazioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Iniettività, suriettività e biiettività
In questo paragrafo elenchiamo alcune proprietà di cui godono certe funzioni.
Funzioni iniettive
Una funzione 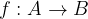 si dice iniettiva se ogni elemento di B è immagine di al più un elemento di A.
si dice iniettiva se ogni elemento di B è immagine di al più un elemento di A.
In pratica una funzione è iniettiva se a due elementi distinti del dominio corrispondono due immagini distinte:
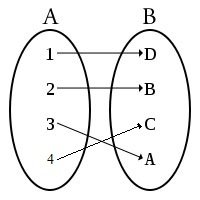
Riportiamo il diagramma a frecce di una funzione iniettiva: notiamo che a ogni elemento dell'insieme B arriva al più una freccia (ossia, ne possono arrivare o una o nessuna).
Funzioni suriettive
Una funzione 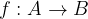 si dice suriettiva se ogni elemento di B è immagine di almeno un elemento di A.
si dice suriettiva se ogni elemento di B è immagine di almeno un elemento di A.
Possiamo anche dire che una funzione è suriettiva se l'insieme immagine, ossia l'insieme degli elementi di B che sono immagine di un qualche elemento 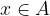 , coincide con l'intero codominio B della funzione.
, coincide con l'intero codominio B della funzione.
Riportiamo il diagramma a frecce di una funzione suriettiva: notiamo che a ogni elemento di B arriva almeno una freccia (ma può arrivargliene anche più di una).
Funzioni biiettive
Una funzione 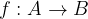 si dice biiettiva o biunivoca se è sia iniettiva sia suriettiva.
si dice biiettiva o biunivoca se è sia iniettiva sia suriettiva.
Riportiamo il diagramma a frecce di una funzione biiettiva: a ogni elemento di B arriva una e una sola freccia.
Composizione di funzioni
possiamo considerare la loro composizione, che consiste nell'applicare in successione prima la funzione f e poi la funzione g:
La funzione composta di f e g si indica con il simbolo 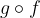 , ed è una funzione dall'insieme A all'insieme C, che agisce applicando ad ogni elemento x in A dapprima la funzione f, e poi applicando al valore f(x) così ottenuto la funzione g, come se leggessimo il segno
, ed è una funzione dall'insieme A all'insieme C, che agisce applicando ad ogni elemento x in A dapprima la funzione f, e poi applicando al valore f(x) così ottenuto la funzione g, come se leggessimo il segno 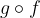 da destra verso sinistra.
da destra verso sinistra.
L'immagine di x tramite la funzione composta 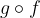 si scrive
si scrive 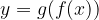 e si legge "g di f di x".
e si legge "g di f di x".
L'operazione di composizione di funzioni non è commutativa.
Se facciamo 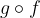 , ossia applichiamo prima f e poi g, otteniamo qualcosa di diverso da ciò che otterremmo facendo
, ossia applichiamo prima f e poi g, otteniamo qualcosa di diverso da ciò che otterremmo facendo 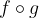 , ossia applicando prima g e poi f (ammesso che esistano entrambe le funzioni composte):
, ossia applicando prima g e poi f (ammesso che esistano entrambe le funzioni composte):
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




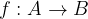
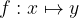
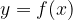
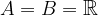
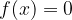
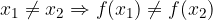
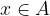 , coincide con l'intero codominio B della funzione.
, coincide con l'intero codominio B della funzione.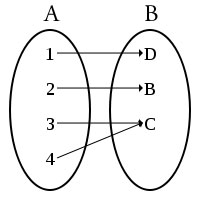
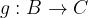
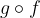 , ed è una funzione dall'insieme A all'insieme C, che agisce applicando ad ogni elemento x in A dapprima la funzione f, e poi applicando al valore f(x) così ottenuto la funzione g, come se leggessimo il segno
, ed è una funzione dall'insieme A all'insieme C, che agisce applicando ad ogni elemento x in A dapprima la funzione f, e poi applicando al valore f(x) così ottenuto la funzione g, come se leggessimo il segno 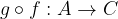
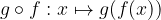
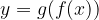 e si legge "g di f di x".
e si legge "g di f di x".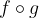 , ossia applicando prima g e poi f (ammesso che esistano entrambe le funzioni composte):
, ossia applicando prima g e poi f (ammesso che esistano entrambe le funzioni composte):