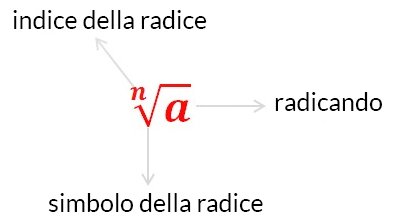
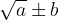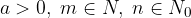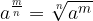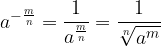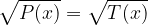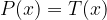Un radicale - o radice - è l'operazione matematica inversa dell'elevamento a potenza. Lo scriviamo in questo modo:
Vediamo la relazione tra una radice e la sua operazione inversa, l'elevamento a potenza.
Vediamo la stessa cosa in un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Anche se aumenta l'indice della radice, non cambia il concetto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radici particolari
Vediamo alcuni casi di radici particolari:
Radice quadrata
La radice di indice 2 è detta radice quadrata e si indica senza esplicitare l’indice.
Possiamo scrivere la radice quadrata omettendo l'indice 2.
Radice cubica
La radice di indice 3 è detta radice cubica:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radice con indice 1
La radice di indice 1 può essere omessa, perchè un un numero elevato alla prima potenza è uguale a se stesso.
Indice dei radicali
E' molto importante considerare l'indice dei radicali, soprattutto se il radicando è negativo. Abbiamo due casi:
radicali con indice pari;
radicali con indice dispari;
Radicali con indice pari
Se la radice ha indice pari il radicando deve essere maggiore o uguale a zero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radicali con indice dispari
Se la radice ha indice dispari il radicando può essere anche negativo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà invariantiva
Il valore di un radicale non cambia se si moltiplicano indice della radice ed esponente del radicando per uno stesso numero, escluso lo 0.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Semplificazione di un radicale
Un radicale si dice irriducibile se l'indice e l'esponente del radicando sono primi tra loro (cioè non si possono semplificare).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Semplificare un radicale significa trasformarlo in un radicale irriducibile, applicando la proprietà invariantiva, cioè dividendo indice ed esponente per il loro M.C.D.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Ci sono alcune difficoltà in più con i radicandi letterali.
Se il radicando è letterale, è necessario imporre sempre la sua positività con l'uso dei valori assoluti.
Riduzione di più radicali allo stesso indice
Per ridurre due o più radicali irriducibili allo stesso indice si procede nel modo seguente:
si determina il minimo comune indice (m.c.i.) e si assume come indice comune ai radicali dati;
come per il minimo comun denominatore, si moltiplicano i vari esponenti dei radicandi;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Operazioni tra radicali
Le operazioni che si possono fare tra i radicali sono:
Moltiplicazione
Si distinguono due casi, a seconda dell'indice dei due radicali.
stesso indice: il risultato è un radicale che mantiene l'indice e ha come radicando il prodotto dei radicandi;
indice diverso: bisogna prima ridurli allo stesso indice e poi eseguire la moltiplicazione;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione
Si distinguono due casi, a seconda dell'indice dei due radicali.
stesso indice: il risultato è un radicale che mantiene l'indice e ha come radicando il prodotto dei radicandi;
indice diverso: bisogna prima ridurli allo stesso indice e poi eseguire la divisione;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Potenza
Per elevare ad una potenza un radicale basta elevare a quella potenza il radicando.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radice di radice
La radice n-esima di una radice m-esima è una radice nm-esima.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma algebrica
La somma algebrica di due radici simili è una radice simile a quelle di partenza avente per coefficiente la somma algebrica dei coefficienti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La somma algebrica dei radicali è quindi molto simile a quella dei monomi.
Due radicali sono simili se hanno lo stesso indice e lo stesso radicando.
In questo caso infatti la somma non si può eseguire perché i radicali non sono simili.
Trasporto di un fattore fuori dal segno di radice
Ricordiamo la moltiplicazione tra radici:
Questo può servirci per portare qualche fattore fuori dalla radice. Immaginiamo di avere una situazione tipo:
Avendo dentro la radice quadrata un fattore elevato alla seconda possiamo possiamo portarlo fuori dalla radice.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quando si portano fuori radice termini letterali occorre farlo con molta attenzione, infatti:
se l'indice n è pari, il radicando che viene portato fuori, dovrà imporsi positivo, quindi è bene estrarlo in valore assoluto;
se l'indice n è dispari, non occorre farlo, perché in questo caso, avere un radicando positivo o negativo sarà del tutto indifferente.
Il trasporto fuori radice può risultare utile per eseguire una somma di radicali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trasporto di un fattore sotto il segno di radice
Per portare sotto radice un fattore occorre elevarlo ad una potenza uguale all'indice della radice. Dobbiamo stare attenti all'indice della radice, se ci troviamo di fronte a fattori negativi da portare sotto radice.
Nel caso di indice dispari non ci sono particolari problemi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nel caso di indici pari dobbiamo prestare attenzione. Nel caso in cui fuori dalla radice si trovi un fattore negativo possiamo trasportare sotto il segno di radice il suo valore assoluto lasciando fuori il segno "-"
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Razionalizzazione del denominatore di una frazione
La razionalizzazione è la trasformazione di una frazione contenente radicali al denominatore in un’altra equivalente priva di radicali al denominatore.
Per razionalizzare una frazione si moltiplica il numeratore e il denominatore per una stessa espressione il cui valore numerico è 1 e la cui scelta dipende dalla forma del denominatore che si vuole razionalizzare.
Radicale quadratico
Con un radicale del tipo 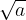 al denominatore dobbiamo moltiplicare numeratore e denominatore per il radicale quadratico che figura a denominatore, cioè
al denominatore dobbiamo moltiplicare numeratore e denominatore per il radicale quadratico che figura a denominatore, cioè 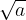
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radicale non quadratico
In caso di denominatore del tipo 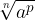 , si distinguono due casi:
, si distinguono due casi:
quando 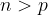 , occorre moltiplicare numeratore e denominatore per il radicale
, occorre moltiplicare numeratore e denominatore per il radicale 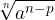
quando 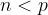 , prima di razionalizzare, è opportuno operare il trasporto fuori radice come visto nei paragrafi precedenti.
, prima di razionalizzare, è opportuno operare il trasporto fuori radice come visto nei paragrafi precedenti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma o differenza di radicali quadratici
Se il denominatore è del tipo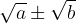 occorrerà moltiplicare numeratore e denominatore per il coniugato
occorrerà moltiplicare numeratore e denominatore per il coniugato 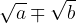
Analogo procedimento si adotta anche quando al denominatore si presentano forme del tipo 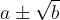 oppure
oppure 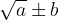
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Potenze ad esponente frazionario
Possiamo indicare un radicale con una potenza avente:
base uguale al radicando;
come esponente una frazione con al numeratore l'esponente del radicando ed al denominatore l'indice della radice.
Vediamo come sono definite le potenze ad esponente frazionario.
le potenze ad esponente frazionario sono così definite:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sfruttando la seconda definizione, deduciamo che il reciproco di una potenza si ottiene banalmente cambiando il segno al suo esponente. Vediamo un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazioni irrazionali
Un'equazione è irrazionale se, almeno una volta, l'incognita figura sotto il segno di radice. Per risolverla occorre trasformarla in un'altra equazione equivalente non contenente radicali mediante elevamenti a potenza di ambo i membri.
Quindi, considerando come esempio P(x) e T(x) due qualsiasi polinomi, in presenza di un'equazione del genere
Si elevano al quadrato entrambi i membri e l'equazione da risolvere diventa:




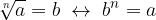
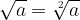
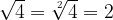
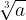
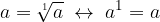
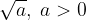
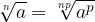
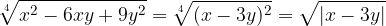
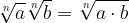
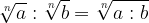
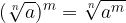
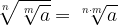
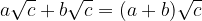
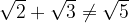
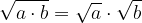
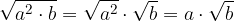
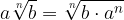
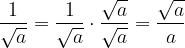
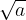 al denominatore dobbiamo moltiplicare numeratore e denominatore per il radicale quadratico che figura a denominatore, cioè
al denominatore dobbiamo moltiplicare numeratore e denominatore per il radicale quadratico che figura a denominatore, cioè 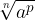 , si distinguono due casi:
, si distinguono due casi: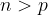 , occorre moltiplicare numeratore e denominatore per il radicale
, occorre moltiplicare numeratore e denominatore per il radicale 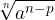
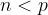 , prima di razionalizzare, è opportuno operare il trasporto fuori radice come visto nei paragrafi precedenti.
, prima di razionalizzare, è opportuno operare il trasporto fuori radice come visto nei paragrafi precedenti.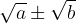 occorrerà moltiplicare numeratore e denominatore per il coniugato
occorrerà moltiplicare numeratore e denominatore per il coniugato 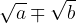
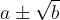 oppure
oppure