Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





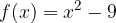
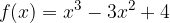
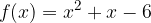
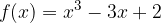
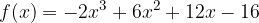
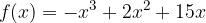
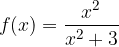
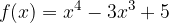
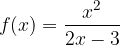
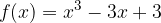
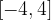
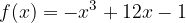
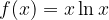
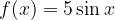
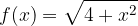
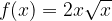
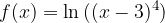
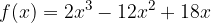
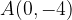
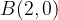
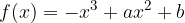 passi per i punti A e B. Calcolare, inoltre, i punti stazionari della funzione.
passi per i punti A e B. Calcolare, inoltre, i punti stazionari della funzione.


