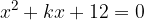Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





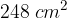 . Calcolare il perimetro del rettangolo sapendo che la differenza fra la base e l'altezza è
. Calcolare il perimetro del rettangolo sapendo che la differenza fra la base e l'altezza è 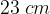 .
.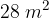 .
.
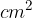 . Determinare il perimetro del rettangolo.
. Determinare il perimetro del rettangolo.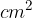 . Determinare le misure dei lati del rettangolo.
. Determinare le misure dei lati del rettangolo.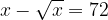
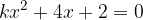
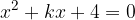
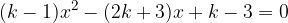
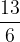 .
.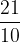 .
.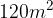 .
.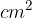 .
.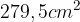 ed suddiviso in un quadrato ed un rettangolo (come mostrato in figura). Il lato del rettangolo più piccolo è 4,5 cm inferiore del lato del quadrato.
ed suddiviso in un quadrato ed un rettangolo (come mostrato in figura). Il lato del rettangolo più piccolo è 4,5 cm inferiore del lato del quadrato.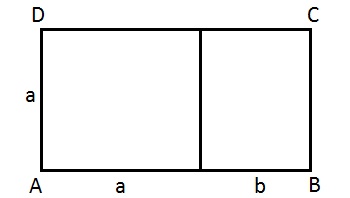
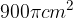 e la distanza del centro dal punto medio della corda è uguale alla misura della corda meno 30cm.
e la distanza del centro dal punto medio della corda è uguale alla misura della corda meno 30cm.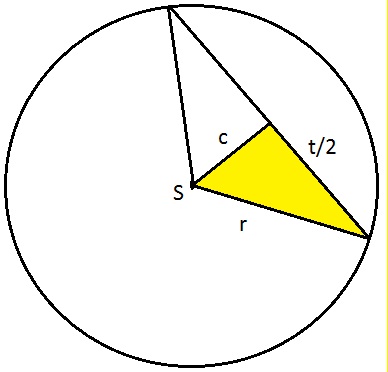
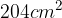 ed un lato supera l'altro di 5 cm.
ed un lato supera l'altro di 5 cm.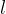 ed
ed 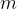 .
.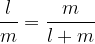
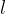 ed
ed 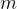 .
.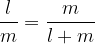
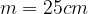 .
.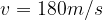 e con una alzata
e con una alzata 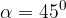 rispetto al piano orizzontale.
rispetto al piano orizzontale.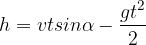
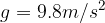 .
.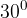 e ad una velocità iniziale
e ad una velocità iniziale 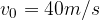 . La freccia effettua una traiettoria parabolica.
. La freccia effettua una traiettoria parabolica.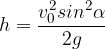
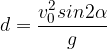
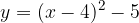
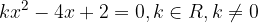
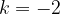 ;
;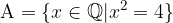
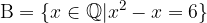
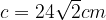
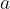 e
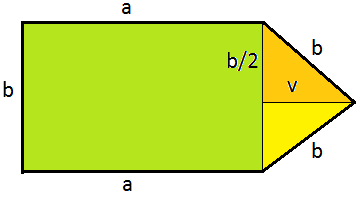
e 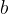 (vedi figura).
(vedi figura).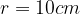
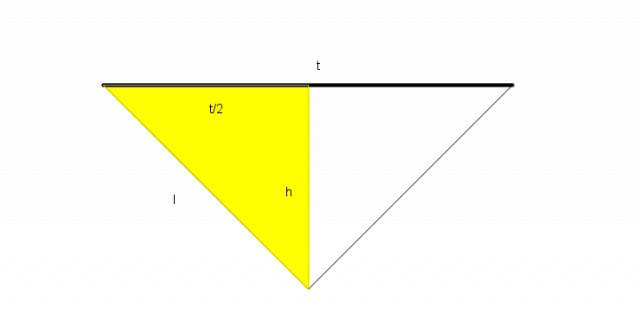
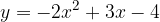
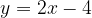
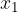 ed
ed 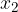
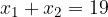
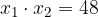
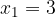
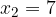
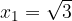
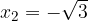
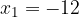
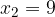
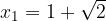
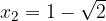
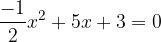
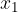 ed
ed 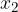
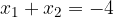
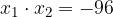
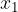 ed
ed 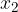
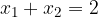
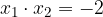
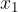 ed
ed 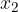
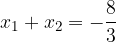
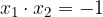
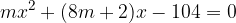
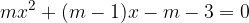
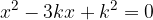
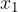 ed
ed 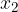 le soluzioni, trova il valore del parametro k in modo che la somma dei quadrati delle soluzioni sia pari a
le soluzioni, trova il valore del parametro k in modo che la somma dei quadrati delle soluzioni sia pari a 
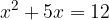
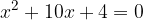
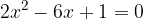
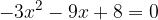
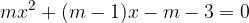
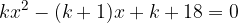
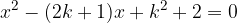
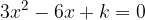
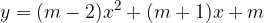 ;
;