Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





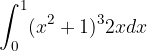 .
.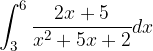
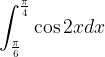
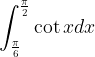 .
.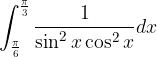
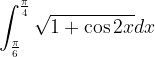 .
.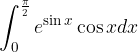
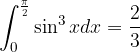
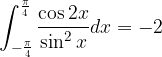
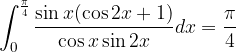
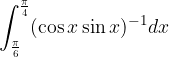
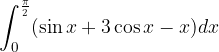
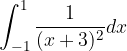
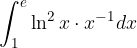


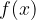 :
: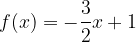
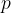 . Disegnare il grafico della funzione
. Disegnare il grafico della funzione 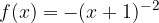 .
.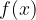 è crescente nell'intervallo
è crescente nell'intervallo 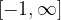 .
.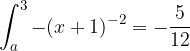 ?
?
 nel punto di ascissa
nel punto di ascissa 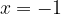 .
.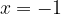 .
. .
.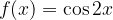 ,
,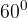 .
.

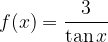 .
.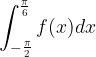 .
.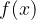 nel punto
nel punto 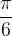 .
. .
.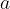 , tale che
, tale che 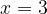 sia uno zero del polinomio e poi determinarne i restanti zeri.
sia uno zero del polinomio e poi determinarne i restanti zeri.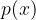 e dall'asse delle ascisse.
e dall'asse delle ascisse.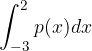 della funzione
della funzione 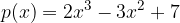 con il valore minimo
con il valore minimo 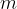 e il valore massimo
e il valore massimo 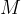 che tale funzione assume nell'intervallo
che tale funzione assume nell'intervallo 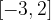 .
.


