Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




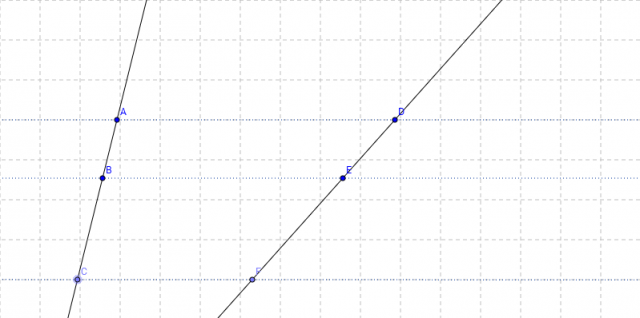
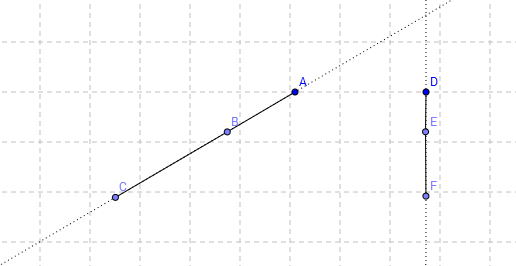
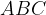 , sia
, sia 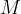 il punto medio del lato
il punto medio del lato 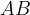 e
e 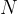 il punto medio del lato
il punto medio del lato 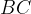 . Verificare che il segmento
. Verificare che il segmento 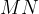 è parallelo alla base
è parallelo alla base 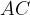 .
.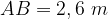
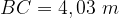
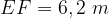
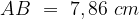 ,
, 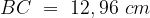 ,
, 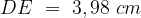 ,
, 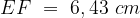
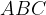 , la bisettrice di ciascun angolo divide il lato opposto in segmenti proporzionali agli altri due lati in modo che ciascun segmento corrisponda al lato con il quale ha un vertice in comune.
, la bisettrice di ciascun angolo divide il lato opposto in segmenti proporzionali agli altri due lati in modo che ciascun segmento corrisponda al lato con il quale ha un vertice in comune.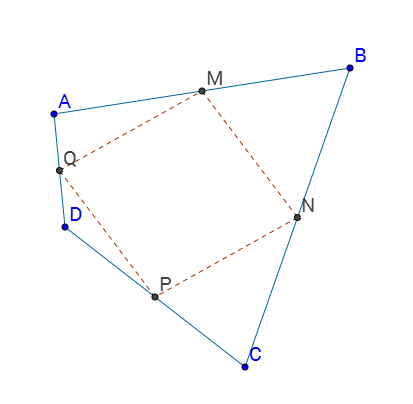
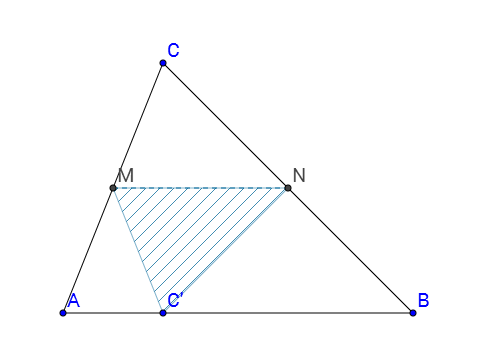
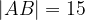 e
e 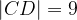 , mentre i lati obliqui hanno lunghezza 5.
, mentre i lati obliqui hanno lunghezza 5.


