Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





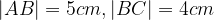 .
.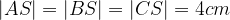
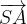 ,
, 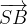 ed
ed 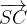 . Tali vettori sono gli stessi?
. Tali vettori sono gli stessi?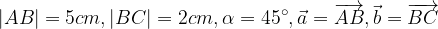 .
. ?
?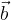
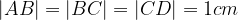 (unità).
(unità).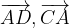 e
e 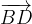
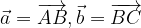 e
e 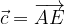 .
.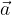
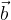
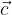
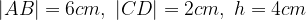
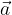 e
e 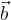 non sono colineari:
non sono colineari: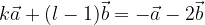
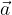 e
e 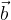 non sono colineari:
non sono colineari: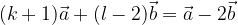
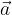 e
e 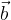 non sono allineati:
non sono allineati: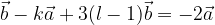
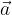 e
e 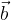 non sono allineati:
non sono allineati: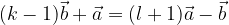
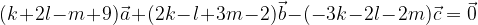
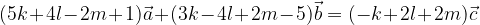
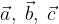
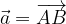 lungo 5 cm, scrivere e disegnare un vettore unitario
lungo 5 cm, scrivere e disegnare un vettore unitario 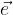 avente la stessa direzione del vettore
avente la stessa direzione del vettore 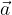 .
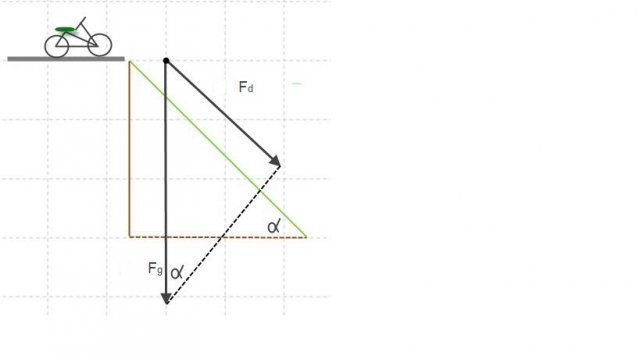
.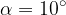 scende un ciclista.
scende un ciclista.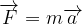 e le equazioni
e le equazioni 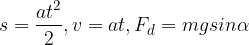 .
.