Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





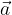 e
e 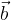 sono colineari se sono paralleli o giacciono su linee parallele.
sono colineari se sono paralleli o giacciono su linee parallele.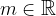 tale che:
tale che: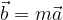
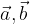 e
e 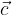 sono complanari, esistono
sono complanari, esistono 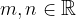 tali che:
tali che: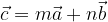
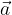 e
e 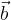 è scritta come:
è scritta come: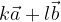
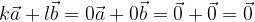
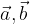 e
e 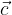 si esprime come la somma dei tre vettori moltiplicati per i numeri reali k, l ed m:
si esprime come la somma dei tre vettori moltiplicati per i numeri reali k, l ed m: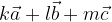
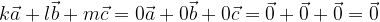
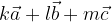
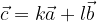
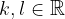 .
.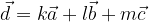
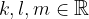
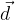 ) utilizzando i vettori di base (ad esempio
) utilizzando i vettori di base (ad esempio 


