Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





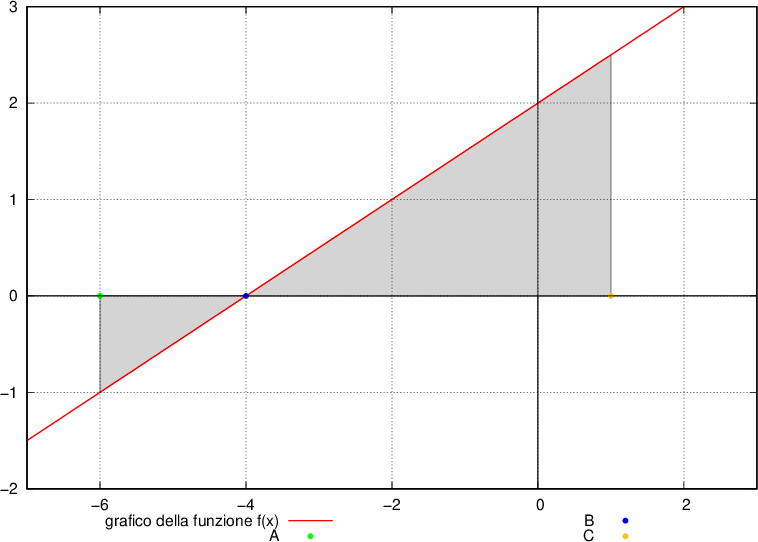
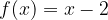 .
.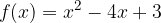 e l'asse delle ascisse.
e l'asse delle ascisse.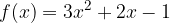 e l'asse delle ascisse
e l'asse delle ascisse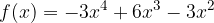 e l'asse delle ascisse.
e l'asse delle ascisse.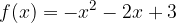 e l'asse delle ascisse.
e l'asse delle ascisse.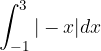 , tenendo presente che rappresenta l'area della superficie piana compresa tra la curva descritta dalla funzione
, tenendo presente che rappresenta l'area della superficie piana compresa tra la curva descritta dalla funzione 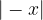 e l'asse delle ascisse.
e l'asse delle ascisse.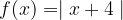 e dall'asse delle ascisse nell'intervallo
e dall'asse delle ascisse nell'intervallo 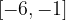 .
.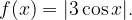
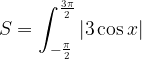 .
.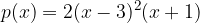 e dall'asse delle ascisse.
e dall'asse delle ascisse.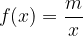 , trovare il valore di m sapendo che l'area della superficie piana delimitata dalla curva f(x) e l'asse delle ascisse nell'intervallo
, trovare il valore di m sapendo che l'area della superficie piana delimitata dalla curva f(x) e l'asse delle ascisse nell'intervallo 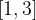 è uguale a
è uguale a 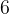 .
.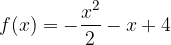 e l'asse delle ascisse nell'intervallo
e l'asse delle ascisse nell'intervallo 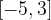 .
.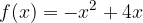 , la retta
, la retta 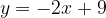 e l'asse delle ascisse.
e l'asse delle ascisse.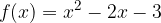 e la retta
e la retta 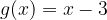 .
.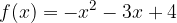 e
e 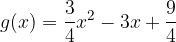 .
.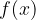 e
e 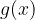
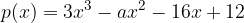 .
.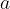 , tale che
, tale che 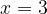 sia uno zero del polinomio e poi determinarne i restanti zeri.
sia uno zero del polinomio e poi determinarne i restanti zeri.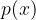 e dall'asse delle ascisse.
e dall'asse delle ascisse.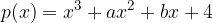 :
: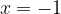 , il polinomio
, il polinomio 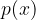 sia nullo e che tale punto rappresenti anche un estremo locale della funzione.
sia nullo e che tale punto rappresenti anche un estremo locale della funzione.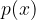 . Disegnarne il grafico.
. Disegnarne il grafico.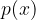 e gli assi cartesiani.
e gli assi cartesiani.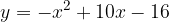 e la retta
e la retta 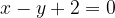
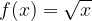
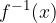 .
.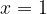 e
e 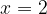 , e dalla curva
, e dalla curva 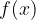
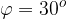 .
.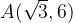 ?
?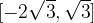 delimita con l'asse delle ascisse una superficie piana la cui area è
delimita con l'asse delle ascisse una superficie piana la cui area è 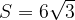 ?
?


