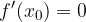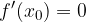In questo capitolo analizziamo come si possono utilizzare le derivate.
Determinazione della tangente alla curva e della normale alla curva
Determinazione della tangente alla curva
Data la funzione 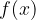 ed il punto
ed il punto 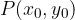 vogliamo determinare la tangente alla curva.
vogliamo determinare la tangente alla curva.
Supponendo di conoscere la funzione 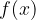 ed il punto
ed il punto 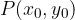 , possiamo scrivere:
, possiamo scrivere:
L'equazione della tangente alla curva 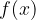 nel punto
nel punto 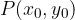 è:
è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Determinazione della normale alla curva
Data la funzione 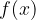 ed il punto
ed il punto 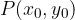 è possibile calcolare la normale alla curva.
è possibile calcolare la normale alla curva.
La normale alla curva è perpendicolare alla tangente alla curva passante per il punto dato, per cui la pendenza della normale è pari all'opposto del reciproco alla pendenza della tangente, cioè:
dove si indica con 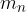 la pendenza della normale, mentre con
la pendenza della normale, mentre con 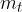 la pendenza della tangente.
la pendenza della tangente.
Supponendo di conoscere la funzione 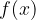 ed il punto
ed il punto 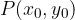 , possiamo scrivere:
, possiamo scrivere:
In definitiva l'equazione della normale alla curva 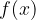 nel punto
nel punto 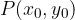 è:
è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Utilizzo della derivata per calcolare gli angoli
Calcolo dell'angolo tra una curva e l'asse della ascisse
Utilizzando il concetto di derivata è possibile calcolare l'angolo formato da una curva 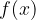 e l'asse delle x.
e l'asse delle x.
Basta considerare l'intersezione della curva con l'asse delle ascisse (in figura il punto 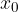 ) e calcolare l'angolo formato dalla tangente alla curva nel punto
) e calcolare l'angolo formato dalla tangente alla curva nel punto 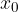 e l'asse delle x.
e l'asse delle x.
Dalla teoria sulle derivate sappiamo che l'angolo cercato è pari al coefficiente angolare della tangente alla curva:
L'angolo formato da una curva 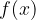 e l'asse delle x è:
e l'asse delle x è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Calcolo dell'angolo tra una curva e l'asse della ordinate
Utilizzando il concetto di derivata è possibile calcolare l'angolo formato da una curva 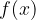 e l'asse delle y.
e l'asse delle y.
Si ricorda dalla geometria che:
Due angoli sono complementari se la loro somma è pari a 90°.
Dal grafico si può notare come gli angolo 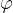 (angolo tra la curva e l'asse delle x) e
(angolo tra la curva e l'asse delle x) e 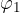 (angolo tra la curva e l'asse delle y) sono complementari:
(angolo tra la curva e l'asse delle y) sono complementari:
Per la complementarietà si ha quindi:
e sapendo calcolare 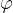 (paragrafo precedente) è possibile trovare
(paragrafo precedente) è possibile trovare 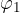 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Angolo tra due curve
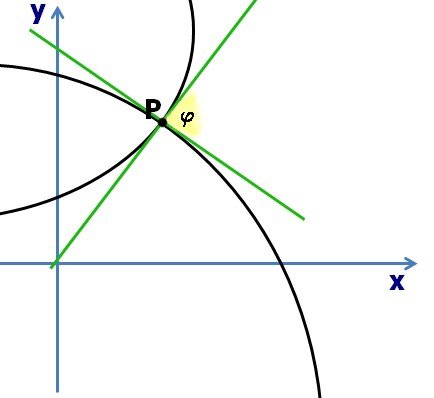
Lo scopo di questo paragrafo è trovare l'angolo racchiuso tra l'intersezione di due curve.
L'angolo cercato è quello che si forma tra le tangenti alle curve calcolate nel punto di intersezione delle curve stesse.
Vediamo il tutto graficamente:
Tale angolo si può calcolare con la seguente formula:
dove 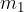 è il coefficiente angolare della prima tangente ed
è il coefficiente angolare della prima tangente ed 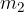 è il coefficiente angolare dell'altra tangente.
è il coefficiente angolare dell'altra tangente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Determinazione della crescenza, decrescenza e dei punti di flesso
Quando si traccia il grafico di una funzione, occorre essere quanto più accurati possibile.
In particolare occorre trovare gli intervalli in cui la funzione cresce, quelli in cui la funzione decresce ed anche i cosiddetti punti stazionari, che saranno analizzati più in dettaglio nel paragrafo successivo.
Partiamo effettuando un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dall'esempio appena svolto notiamo che la funzione tende a decrescere per x<0, successivamente tende a crescere per x>4/3, mentre non sappiamo come si comporta nell'intervallo tra 0 e 4/3.
in quale punto la funzione raggiunge il suo minimo?
da quale punto in poi la funzione inizia a crescere?
la funzione possiede un solo minimo?
Utilizzando la derivata si possono ottenere le risposte alle domande precedenti.
In particolare occorre studiare i minimi ed i massimi locali che vengono chiamati, in generale estremi locali.
Minimi e massimi locali possono anche essere chiamati minimi e massimi relativi.
Allo stesso modo estremi locali possono essere chiamati estremi relativi.
Il più grande dei massimi locali è il massimo globale.
Il più piccolo dei minimi locali è il minimo globale.
E' importante sottolineare che se la funzione f è definita in un intervallo [a, b], allora il minimo o massimo globale può trovarsi negli estremi dell'intervallo, cioè coincidere con f(a) o con f(b).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Crescenza e decrescenza di una funzione
Possiamo dare le seguenti definizioni:
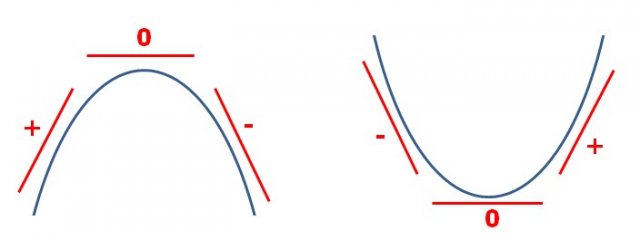
Una funzione è crescente nei punti in cui la derivata della funzione è positiva.
Una funzione è decrescente nei punti in cui la derivata della funzione è negativa.
Il punto 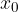 in cui la funzione da crescente passa a decrescente o viceversa è detto estremo locale ed è tale:
in cui la funzione da crescente passa a decrescente o viceversa è detto estremo locale ed è tale:
il che significa che la tangente alla curva nel punto ha pendenza zero, ossia è una retta parallela all'asse delle ascisse.
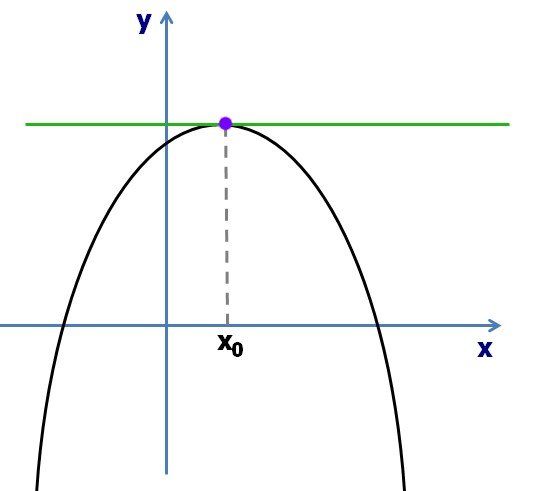
Estremi locali: la pendenza (derivata della funzione) della tangente alla curva uguale a zero
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Punti stazionari
I punti in cui la derivata della funzione è uguale a zero - quindi la tangente è parallela all'asse x - sono chiamati punti stazionari.
I punti stazionari possono essere di tre tipi:
Una funzione f ha in 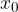 un massimo locale se:
un massimo locale se:
Una funzione f ha in 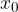 un minimo locale se:
un minimo locale se:
Esistono dei punti in cui la funzione non raggiunge né un massimo né un minimo. Questi punti sono chiamati punti di flesso orizzontale:
Una funzione ha punto stazionario 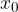 chiamato punto di flesso quando in prossimità del punto la derivata non cambia segno.
chiamato punto di flesso quando in prossimità del punto la derivata non cambia segno.
Problemi estremali
Utilizzando il concetto della derivata si possono risolvere i problemi estremali, quelli in cui è necessario rendere una quantità massima oppure minima, attraverso una funzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





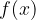 ed il punto
ed il punto 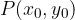 vogliamo determinare la tangente alla curva.
vogliamo determinare la tangente alla curva.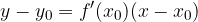
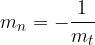
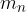 la pendenza della normale, mentre con
la pendenza della normale, mentre con 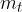 la pendenza della tangente.
la pendenza della tangente.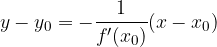
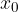 ) e calcolare l'angolo formato dalla tangente alla curva nel punto
) e calcolare l'angolo formato dalla tangente alla curva nel punto 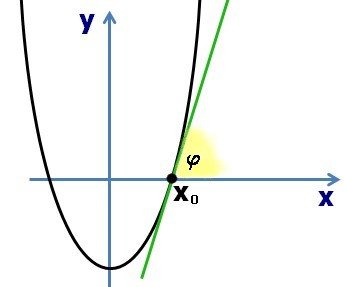
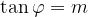
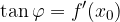
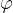 (angolo tra la curva e l'asse delle x) e
(angolo tra la curva e l'asse delle x) e 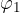 (angolo tra la curva e l'asse delle y) sono complementari:
(angolo tra la curva e l'asse delle y) sono complementari: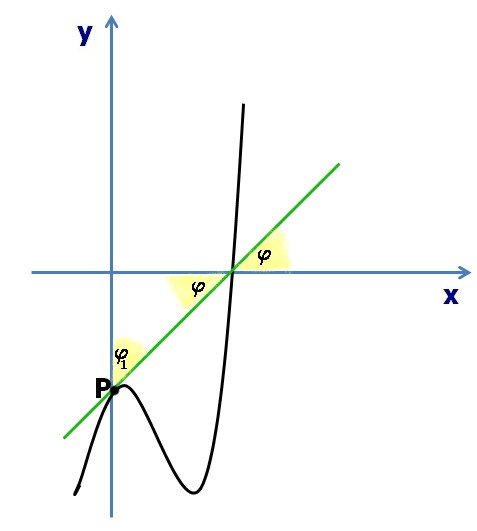
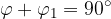
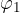 .
.
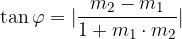
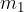 è il coefficiente angolare della prima tangente ed
è il coefficiente angolare della prima tangente ed 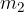 è il coefficiente angolare dell'altra tangente.
è il coefficiente angolare dell'altra tangente.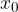 un massimo locale se esiste un intorno completo del punto
un massimo locale se esiste un intorno completo del punto 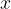 di questo intorno si ha
di questo intorno si ha 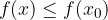 .
.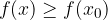 .
.
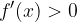 per ogni x appartenente all'intervallo (a,b) allora la funzione
per ogni x appartenente all'intervallo (a,b) allora la funzione 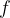 è crescente nell'intervallo.
è crescente nell'intervallo.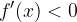 per ogni x appartenente all'intervallo (a,b) allora la funzione
per ogni x appartenente all'intervallo (a,b) allora la funzione