In questo capitolo vedremo un oggetto matematico fondamentale chiamato successione.
Dato un insieme X, una successione in X è un'elencazione ordinata di elementi di X.
Essendo l'argomento vasto, ci limiteremo a studiare un particolare tipo di successione, le successioni nell'insieme 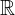 - chiamate successioni reali - e accenneremo alle successioni nell'insieme
- chiamate successioni reali - e accenneremo alle successioni nell'insieme 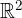 - dette successioni nel piano.
- dette successioni nel piano.
Definizione
Essendo funzioni molto particolari, alcuni elementi hanno nomi propri:
Il termine n-esimo della successione 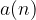 è chiamato termine generale.
è chiamato termine generale.
L'insieme immagine 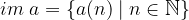 è chiamato supporto della successione.
è chiamato supporto della successione.
Scriviamo il termine generale in questo modo:
Per indicare l'intera successione possiamo usare un elenco:
Oppure una forma analitica:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Grafico di una successione reale
Data una successione reale 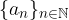 , l' insieme
, l' insieme
è il grafico della successione: esso consiste delle coppie indice-termine della successione.
Vi sono 2 modi per disegnare il grafico di una successione:
grafico cartesiano: in un piano cartesiano si evidenziano punti che hanno per ascissa un indice e per ordinata il termine corrispondente della successione con quell'indice;
retta numerica: nella retta reale si evidenziano punti indicizzati che hanno per ascissa un termine corrispondente della successione;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni ricorsive reali
Spesso una successione non è presentata con il termine generale in funzione dell'indice, ma è funzione dei termini precedenti della successione, ovvero per conoscere l' n-esimo termine della successione ho bisogno di "combinare" i termini precedenti. In tal caso la successione è ricorsiva o definita per ricorrenza.
Per essere più precisi, una successione ricorsiva è una funzione:
il termine generale è legato ai precedenti proprio da questa funzione:
I termini 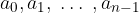 devono essere noti.
devono essere noti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni (il)limitate
Essendo i numeri reali ordinati ha senso parlare di successioni "confinate" (o meno) in certi intervalli della retta reale.
Successioni reali limitate a destra
Ci sono particolari successioni reali in cui tutti i termini sono minori di un certo numero reale costante.
Una successione reale 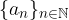 è limitata a destra (o superiormente) se:
è limitata a destra (o superiormente) se:
Ovvero se tutti i termini della successione sono maggiorati da un numero reale costante.
Dato un maggiorante M per una successione limitata a destra, anche tutti i numeri reali maggiori di esso sono ancora maggioranti per tale successione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali limitate a sinistra
Ci sono particolari successioni reali in cui tutti i termini sono maggiori di un certo numero reale costante.
Una successione reale 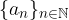 è limitata a sinistra (o inferiormente) se:
è limitata a sinistra (o inferiormente) se:
ovvero tutti i termini della successione sono minorati da un numero reale costante.
Dato un minorante m per una successione limitata a sinistra, anche tutti i numeri reali minori di esso sono ancora minoranti per tale successione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali limitate
Alcune successioni reali limitate a destra (sinistra) sono limitate anche a sinistra (destra).
Una successione reale 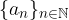 è limitata se è limitata a destra ed a sinistra.
è limitata se è limitata a destra ed a sinistra.
Anche se diversa, la seguente definizione è equivalente alla precedente:
Una successione reale 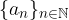 è limitata se
è limitata se 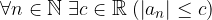 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali monotone
I numeri reali sono ordinati quindi possiamo parlare di ordine tra i termini di una successione. In generale i termini di una successione reale non sono ordinati.
Consideriamo la successione reale:
Tale elenco di numeri reali non è ordinato:
Anzi, l'ordine viene invertito ogni volta passiamo alla coppia successiva di termini vicini!
Tuttavia vi sono successioni reali particolari che si presentano come elenchi ordinati di numeri reali: si chiamano successioni reali monotone.
Cominciamo con quelle in cui i termini elencati diventano sempre più grandi.
Successioni reali crescenti
Ci sono particolari successioni reali in cui i termini sono elencati in modo che più aumentiamo l'indice, maggiore diventa il termine.
Una successione reale 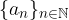 è crescente se
è crescente se 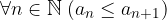 ovvero se ogni termine della successione è maggiore o uguale del precedente.
ovvero se ogni termine della successione è maggiore o uguale del precedente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali strettamente crescenti
Ci sono particolari successioni reali in cui i termini sono elencati in modo che più aumentiamo l'indice, maggiore strettamente diventa il termine.
Una successione reale 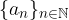 è strettamente crescente se
è strettamente crescente se 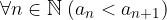 ovvero se ogni termine della successione è maggiore del precedente.
ovvero se ogni termine della successione è maggiore del precedente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali decrescenti
Ci sono particolari successioni reali in cui i termini sono elencati in modo che più aumentiamo l'indice, minore diventa il termine.
Una successione reale 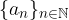 è decrescente se
è decrescente se 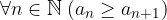 ovvero se ogni termine della successione è minore o uguale del precedente.
ovvero se ogni termine della successione è minore o uguale del precedente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali strettamente decrescenti
Ci sono particolari successioni reali in cui i termini sono elencati in modo che più aumentiamo l'indice, minore strettamente diventa il termine.
Una successione reale 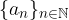 è strettamente decrescente se
è strettamente decrescente se 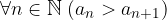 ovvero se ogni termine della successione è minore del precedente.
ovvero se ogni termine della successione è minore del precedente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni reali costanti e quasi-costanti
Particolarmente utili ed importanti sono le successioni reali che assumono sempre (o quasi) il medesimo valore.
Successioni reali costanti
Ci sono particolari successioni reali in cui i termini sono tutti uguali ad un medesimo numero reale.
Una successione reale 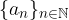 è costante se
è costante se 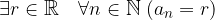 ovvero se ogni termine della successione è sempre uguale ad un numero reale fissato.
ovvero se ogni termine della successione è sempre uguale ad un numero reale fissato.
Il grafico di una successione reale costante è caratterizzato dal fatto che tutti i punti hanno medesima ordinata.
Successioni reali quasi-costanti
Ci sono particolari successioni reali in cui i termini sono quasi tutti uguali ad un medesimo numero reale, ovvero sono tutti uguali ad un medesimo numero reale eccetto un numero finito di termini che assumono un valore arbitrario.
Una successione reale 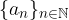 è quasi-costante se:
è quasi-costante se:
ovvero la successione è costante eccetto un numero finito di punti.
Il grafico di una successione reale quasi-costante è caratterizzato dal fatto che "assomiglia" a quello di una successione reale costante eccetto un numero finito di "eccezioni".
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un metodo facile per creare successioni reali quasi-costanti consiste nel prendere una successione costante e modificare il valore di un numero finito di termini.
Segno
I numeri reali sono positivi o negativi quindi possiamo calcolare il segno assunto dai termini di una successione.
Successioni definite
Sia 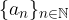 una successione reale. Se per ogni
una successione reale. Se per ogni 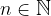 accade che:
accade che:
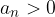 allora la successione è detta a termini strettamente positivi, definita positiva o semplicemente strettamente positiva;
allora la successione è detta a termini strettamente positivi, definita positiva o semplicemente strettamente positiva;
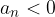 allora la successione è detta a termini strettamente negativi, definita negativa o semplicemente strettamente negativa;
allora la successione è detta a termini strettamente negativi, definita negativa o semplicemente strettamente negativa;
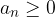 allora la successione è detta a termini positivi, semi-definita positiva o semplicemente positiva;
allora la successione è detta a termini positivi, semi-definita positiva o semplicemente positiva;
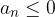 allora la successione è detta a termini negativa, semi-definita negativa o semplicemente negativa;
allora la successione è detta a termini negativa, semi-definita negativa o semplicemente negativa;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il grafico di una successione reale definita o semi-definita è caratterizzato dal fatto che le ordinate di tutti i punti giacciono in uno dei due semipiani individuati dall'asse delle ascisse.
Successioni a segno alterno
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il grafico di una successione reale a segno alterno è caratterizzato dal fatto che le ordinate sono alternatamente positive e negative.
Successioni non definite
Una successione reale 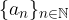 che non sia definita né a segno alterno la chiameremo non definita.
che non sia definita né a segno alterno la chiameremo non definita.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sottosuccessioni
Data una successione reale 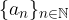 si possono estrarre molto successioni da essa semplicemente prendendo un po' di termini:
si possono estrarre molto successioni da essa semplicemente prendendo un po' di termini:
Dove f è una qualunque funzione dai numeri naturali in sé:
Ricordando la definizione di successione, la funzione b non è altro che la composizione di a dopo f:
Tuttavia una successione costruita in questo modo non conserva generalmente alcuna proprietà della successione di partenza. Nessuno potrebbe impedirci di scegliere sempre il medesimo termine così da rendere la successione costante!
Per evitare questo problema una prima proposta potrebbe essere quella di scegliere termini diversi della successione data - ovvero imporre che f sia iniettiva. Tuttavia questa scelta non è sufficiente per poter conservare le proprietà della successione originale.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Ci sembra ragionevole definire una sottosuccessione come una successione estratta che prende alcuni termini lasciando invariato l'ordine con cui erano disposti. Per ottenere ciò è sufficiente che la mappa f sia strettamente crescente.
Data una successione reale 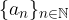 , una sua sottosuccessione è una successione della forma:
, una sua sottosuccessione è una successione della forma:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà delle successioni
Tra le proprietà introdotte finora godute da una successione vi sono delle strette inter-connessioni:
Una successione reale è costante se e solo se è crescente e decrescente.
Una successione reale costante è quasi-costante.
Una successione quasi-costante è limitata.
Una successione strettamente crescente è crescente.
Una successione strettamente decrescente è decrescente.
Una successione strettamente crescente o decrescente è una funzione iniettiva.
Operazioni con le successioni
se la successione 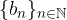 non è mai nulla;
non è mai nulla;
se la successione 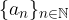 è strettamente positiva;
è strettamente positiva;
Nel caso una delle due successioni sia costante allora possiamo dedurre altre operazioni possibili per i numeri reali.
Data una successione reale 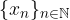 e un numero reale a possiamo definire una nuova successione
e un numero reale a possiamo definire una nuova successione 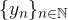 applicando le operazioni usuali termine a termine:
applicando le operazioni usuali termine a termine:
se la successione 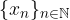 non è mai nulla;
non è mai nulla;
con a numero intero positivo;
con a numero reale strettamente positivo;
Conservazione (o meno) di proprietà
Se le successioni di partenza godono di alcune proprietà, allora vi sono particolari casi in cui possiamo prevedere alcune caratteristiche della successione risultato.
Tramite le operazioni tra successioni è possibile dedurre l'andamento una successione risultato a partire da quelle iniziali:
somme di successioni reali con il medesimo andamento hanno il medesimo andamento;
sommare ad una successione reale monotona una successione costante non ne altera l'andamento;
successioni quasi-costanti reali moltiplicate per una costante sono successioni quasi-costanti;
successioni monotone moltiplicate per costanti positive sono successioni monotone con il medesimo andamento;
successioni monotone moltiplicate per una costanti negative sono successioni monotone con andamento invertito: se (strettamente) crescenti diventano (strettamente) decrescenti e viceversa;
reciproche di successioni monotone mai nulle sono successioni monotone mai nulle con andamento invertito: se (strettamente) crescenti diventano (strettamente) decrescenti e viceversa;
potenze dispari o esponenziali con base maggiore di 1 di successioni (strettamente) monotone sono (strettamente) monotone con il medesimo andamento;
esponenziali di successioni monotone con base minore di 1 sono successioni monotone con andamento invertito: se (strettamente) crescenti diventano (strettamente) decrescenti e viceversa;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Tramite le operazioni tra successioni è possibile dedurre il segno di una successione risultato a partire da quelle iniziali:
somme di successioni (strettamente) positive (negative) sono (strettamente) positive (negative) e sono strettamente positive (negative) se c'è almeno una successione strettamente positiva (negativa);
successioni crescenti (decrescenti) con primo termine (strettamente) positivo (negativo) sono (strettamente) positive (negative);
prodotti di successioni (strettamente) positive sono (strettamente) positivi; prodotti di un numero pari (dispari) di successioni (strettamente) negative sono (strettamente) positivi (negativi);
il prodotto di una successione strettamente positiva (negativa) con una di segno alterno è una successione di segno alterno;
potenze pari (esponenziali) di successioni sono positive (strettamente);
potenze dispari di successioni hanno segno inalterato;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Successioni nel piano
Come detto nell'introduzione, accenneremo qui lo studio di coppie ordinate di successioni reali - ovvero le successioni nel piano.
Definizione
Come per le successioni reali, una successione nel piano è una funzione dai numeri naturali nell'insieme 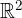 :
:
Guardiamo con più attenzione il supporto di tale successione:
L'elemento 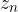 - dato che sta nel prodotto cartesiano dei numeri reali con sé stessi - è una coppia di numeri reali:
- dato che sta nel prodotto cartesiano dei numeri reali con sé stessi - è una coppia di numeri reali:
In generale i numeri reali a e b dipendono dall'indice n:
Dato che la coppia di numeri reali a(n) e b(n) dipendono da n numero naturale - essi fanno parte di una successione reale:
Concludiamo che la successione z in realtà è una coppia ordinata di successioni reali:
Le successioni reali che compongono la successione nel piano hanno dei nomi particolari:
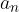 si chiama I componente;
si chiama I componente;
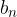 si chiama II componente;
si chiama II componente;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Grafico di una successione nel piano
Come per le successioni reali, se  è una successione del piano, l' insieme
è una successione del piano, l' insieme 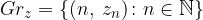 si chiama ancora grafico della successione: esso consiste delle coppie indice-termine della successione.
si chiama ancora grafico della successione: esso consiste delle coppie indice-termine della successione.
Tuttavia essendo il termine della successione due termini ordinati di successioni reali, in realtà si tratta di una terna ordinata indice-I componente-II componente:
Vi sono 2 modi per disegnare il grafico di una successione:
grafico cartesiano: in un spazio cartesiano si evidenziano punti che hanno per ascissa un indice, per ordinata il termine corrispondente della successione con quell'indice come I componente e per altitudine il termine corrispondente della successione con quell'indice come II componente;
piano cartesiano: nel piano cartesiano si evidenziano punti indicizzati che hanno per coordinate un termine corrispondente della successione;
Non useremo il I metodo - anche se lecito - in quanto risulta scomodo e poco intuitivo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





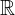 - chiamate successioni reali - e accenneremo alle successioni nell'insieme
- chiamate successioni reali - e accenneremo alle successioni nell'insieme 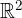 - dette successioni nel piano.
- dette successioni nel piano.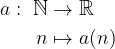
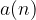 è chiamato termine generale.
è chiamato termine generale.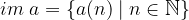 è chiamato supporto della successione.
è chiamato supporto della successione.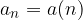
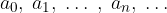
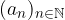
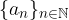 , l' insieme
, l' insieme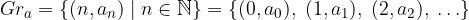
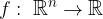
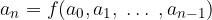
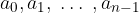 devono essere noti.
devono essere noti.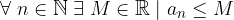
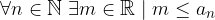
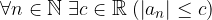 .
.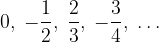
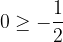
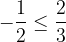
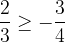
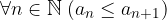 ovvero se ogni termine della successione è maggiore o uguale del precedente.
ovvero se ogni termine della successione è maggiore o uguale del precedente.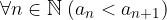 ovvero se ogni termine della successione è maggiore del precedente.
ovvero se ogni termine della successione è maggiore del precedente.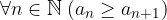 ovvero se ogni termine della successione è minore o uguale del precedente.
ovvero se ogni termine della successione è minore o uguale del precedente.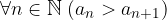 ovvero se ogni termine della successione è minore del precedente.
ovvero se ogni termine della successione è minore del precedente.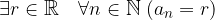 ovvero se ogni termine della successione è sempre uguale ad un numero reale fissato.
ovvero se ogni termine della successione è sempre uguale ad un numero reale fissato.
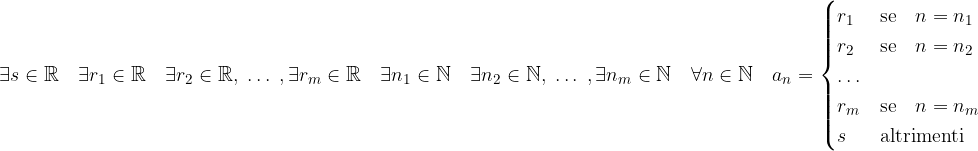
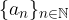 una successione reale. Se per ogni
una successione reale. Se per ogni 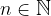 accade che:
accade che: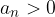 allora la successione è detta a termini strettamente positivi, definita positiva o semplicemente strettamente positiva;
allora la successione è detta a termini strettamente positivi, definita positiva o semplicemente strettamente positiva;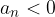 allora la successione è detta a termini strettamente negativi, definita negativa o semplicemente strettamente negativa;
allora la successione è detta a termini strettamente negativi, definita negativa o semplicemente strettamente negativa;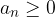 allora la successione è detta a termini positivi, semi-definita positiva o semplicemente positiva;
allora la successione è detta a termini positivi, semi-definita positiva o semplicemente positiva;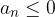 allora la successione è detta a termini negativa, semi-definita negativa o semplicemente negativa;
allora la successione è detta a termini negativa, semi-definita negativa o semplicemente negativa;
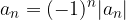 o
o 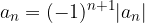 è detta a termini di segno alterno o a segno alterno.
è detta a termini di segno alterno o a segno alterno.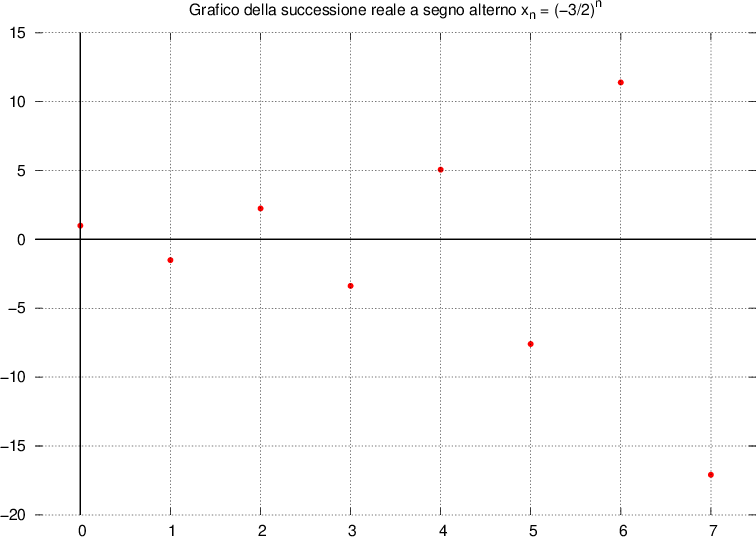
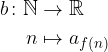
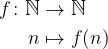
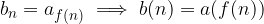
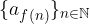
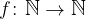 è
è 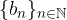 possiamo definire una nuova successione
possiamo definire una nuova successione 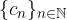 applicando le
applicando le 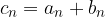
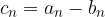
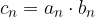
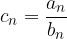
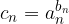
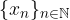 e un numero reale a possiamo definire una nuova successione
e un numero reale a possiamo definire una nuova successione 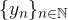 applicando le operazioni usuali termine a termine:
applicando le operazioni usuali termine a termine: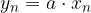
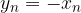
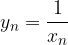
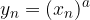
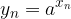
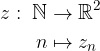
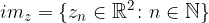
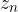 - dato che sta nel prodotto cartesiano dei numeri reali con sé stessi - è una coppia di numeri reali:
- dato che sta nel prodotto cartesiano dei numeri reali con sé stessi - è una coppia di numeri reali: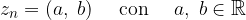
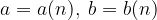
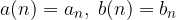
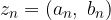
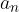 si chiama I componente;
si chiama I componente;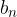 si chiama II componente;
si chiama II componente; è una successione del piano, l' insieme
è una successione del piano, l' insieme 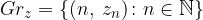 si chiama ancora grafico della successione: esso consiste delle coppie indice-termine della successione.
si chiama ancora grafico della successione: esso consiste delle coppie indice-termine della successione.



