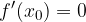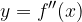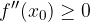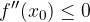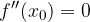In questo capitolo vedremo passo passo come affrontare uno studio di funzione.
L'obiettivo di uno studio di funzione è riuscire a disegnare nel modo più preciso possibile il grafico di una funzione mediante diversi passaggi, ognuno dei quali ci fornisce informazioni in più sulla funzione. Una volta raccolte tutte le proprietà e caratteristiche della funzione, saremo in grado di disegnarne un grafico qualitativo.
Dominio
Prima di tutto dobbiamo vedere per quali x la funzione esiste. In questo modo saremo in grado di escludere le zone del piano cartesiano in cui non passa il grafico.
Il dominio D di una funzione è quel sottoinsieme dei numeri reali in cui la funzione y=f(x) è definita: tutti gli x per cui esistono i corrispondenti valori di y.
C'è una sottile differenza tra dominio e campo di esistenza, seppure negli esercizi che seguono si abuserà del linguaggio considerandoli la stessa cosa.
Come sopra indicato, il dominio è l'insieme in cui è definita la funzione, mentre il campo di esistenza è l'insieme dei valori della x per cui la funzione f(x) ha senso, quindi possiamo dire che il campo di esistenza è il massimo dominio che si può scegliere.
Per esempio il campo di esistenza della funzione 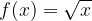 è
è 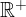 , ma si può scegliere come dominio l'insieme di tutti i reali pari positivi.
, ma si può scegliere come dominio l'insieme di tutti i reali pari positivi.
Per determinare il dominio guardiamo in quali punti o intervalli di 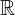 la funzione non è definita, cioè non ha senso calcolarla. In particolare:
la funzione non è definita, cioè non ha senso calcolarla. In particolare:
se ci sono denominatori, vanno posti diversi da zero;
se sono presenti logaritmi, i loro argomenti devono essere strettamente maggiori di zero;
se ci sono radici con indice pari, i radicandi dovranno essere maggiori o uguali a zero.
Una volta determinate tutte le condizioni, dobbiamo metterle a sistema. Risolto il sistema, scriveremo il dominio nella forma di unione di intervalli.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzioni pari e dispari
Vogliamo ora sapere se una funzione è pari, dispari, o nessuna delle due cose. Questo ci può aiutare notevolmente nella realizzazione del grafico in quanto :
se una funzione è pari allora è simmetrica rispetto all'asse delle y
se una funzione è dispari allora è simmetrica rispetto all'origine degli assi (0,0)
Pertanto, se abbiamo una funzione pari basta disegnare la metà a destra o sinistra dell'asse delle y e poi riprodurla specularmente.
Se la funzione è dispari è sufficiente fare una metà di grafico e ribaltarlo prima rispetto all'asse y e poi rispetto all'asse x.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Intersezioni con gli assi
Troviamo i punti di intersezione della funzione con gli assi cartesiani. Per farlo mettiamo a sistema la funzione con l'asse delle x e con quello delle y. Una funzione può avere infiniti punti di intersezione con l'asse x e solo un punto di intersezione con l'asse y.
Per le intersezioni con l'asse delle ascisse determiniamo i punti in cui f(x)=0
Per l'intersezione con l'asse delle ordinate calcoliamo il valore di f(0)
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Studio del segno
Dopo aver determinato le intersezioni con gli assi, procediamo cercando di capire in quali parti del piano passa il grafico, cioè in quali intervalli del suo dominio il grafico della funzione y=f(x) si trova al di sopra o al di sotto dell'asse delle ascisse; per farlo dobbiamo studiarne il segno, cioè risolvere la disequazione:
Nelle intersezioni con l'asse delle x, la funzione cambia segno.
Ricordiamo sempre di scartare le eventuali soluzioni che non rientrano nel dominio della funzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Limiti agli estremi del dominio e ricerca degli asintoti
Quando il campo di esistenza è diverso da tutto 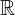 e vi sono delle zone in cui la funzione non è definita, dobbiamo controllare qual è il valore della funzione nei punti che separano queste zone.
e vi sono delle zone in cui la funzione non è definita, dobbiamo controllare qual è il valore della funzione nei punti che separano queste zone.
Con estremi del dominio si intendono i "confini" del dominio della funzione y=f(x) considerata, quindi i punti "ai bordi" del dominio, punti in cui la funzione non è definita, inclusi eventualmente 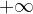 e
e 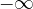 .
.
Per capire come si comporta una funzione in prossimità, cioè in un "intorno", di questi punti, dobbiamo calcolarne il limite (destro, sinistro o completo, facendo attenzione a calcolare il limite solo dalla parte dove la funzione è definita)
Asintoti orizzontali e obliqui
Vediamo per prima cosa quello che fa la funzione all'infinito (se nel dominio): in questo modo possiamo verificare se esistono asintoti obliqui od orizzontali.
Sappiamo che un asintoto orizzontale è una retta parallela all'asse delle x che approssima l'andamento di una funzione all'infinito quindi, per vedere se una data funzione y=f(x) ha uno, due o nessun asintoto orizzontale dovremo calcolare:
Se uno o entrambi questi limiti sono finiti allora avremo uno o due asintoti orizzontali la cui equazione è data proprio dal valore finito ottenuto, altrimenti non avremo asintoti orizzontali.
Un asintoto obliquo è una retta qualsiasi che approssima l'andamento di una assegnata funzione all'infinito; vediamo come verificare se esiste.
Supponiamo che tale asintoto esista, e che abbia equazione y=mx+q; in tal caso allora dalla sua definizione dovrà essere:
Nel caso quindi in cui uno o entrambi i limiti all'infinito della funzione f(x) siano infiniti, calcoleremo quindi gli stessi limiti per f(x)/x.
Il valore che otterremo, se finito, potrebbe essere il coefficiente angolare dell'asintoto in questione. Se infinito invece, concluderemo che non esiste asintoto obliquo.
Se q è un valore finito, avremo ottenuto l'equazione dell'asintoto, altrimenti concluderemo che non esistono asintoti obliqui per la funzione data.
Asintoti verticali e punti di discontinuità
Vediamo ora come si comporta la funzione in prossimità dei punti "critici" del dominio.
Il limite per x tendente ai suddetti valori finiti ci dirà se siamo in presenza di asintoti verticali o altri punti di discontinuità.
Se i due limiti destro e sinistro nel punto in oggetto sono infiniti ci troveremo in presenza di asintoti verticali, la cui equazione è data dalla retta determinata dal punto "critico".
Questo è un caso particolare di "discontinuità di seconda specie", che si ha quando i due limiti destro e sinistro non esistono o sono infiniti.
Se i due limiti destro e sinistro esistono finiti ma non coincidono, si parla di "discontinuità di prima specie".
Se i due limiti sono finiti e coincidono, ma non corrispondono al valore della funzione in quel punto, si parla in questo caso di "discontinuità di terza specie o eliminabile".
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Studio della derivata prima della funzione
Il prossimo passo che dobbiamo affrontare è vedere dove la funzione è crescente e decrescente, e determinare i punti in cui cambia pendenza. Dobbiamo cioè vedere se esistono i punti di massimo/minimo relativo o assoluto. Per fare questo calcoliamo la derivata prima della funzione
e determiniamone il dominio. Dopodiché risolviamo la seguente disequazione
Vediamo le definizioni e i teoremi che ci permetteranno di ottenere quanto cerchiamo.
Monotonia
Sapendo che la derivata in un punto rappresenta il coefficiente angolare (pendenza) della tangente al grafico in quel punto, una funzione sarà crescente quando la derivata è positiva, e decrescente quando tale derivata è negativa.
Teorema fondamentale per funzioni crescenti (decrescenti)
Se 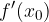 è positiva (negativa) allora la funzione è crescente (decrescente) nel punto, e viceversa.
è positiva (negativa) allora la funzione è crescente (decrescente) nel punto, e viceversa.
Come anticipato, ne segue che la funzione sarà rispettivamente crescente / decrescente in ogni punto del dominio in cui la sua derivata prima sarà positiva / negativa.
Massimi e Minimi
Nei punti in cui la funzione cambia monotonia avremo i massimi o minimi relativi o assoluti.
Vediamone le definizioni e i teoremi necessari per la loro determinazione.
Massimo e minimo assoluto di una funzione
Sia 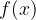 una funzione definita nel suo dominio.
una funzione definita nel suo dominio.
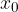 è l'ascissa del punto di massimo (minimo) assoluto se
è l'ascissa del punto di massimo (minimo) assoluto se 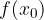 è il valore più grande (piccolo) che la funzione assume nel suo dominio.
è il valore più grande (piccolo) che la funzione assume nel suo dominio.
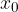 è detto estremante massimante / minimante
è detto estremante massimante / minimante
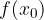 è detto massimo / minimo
è detto massimo / minimo
Massimo e minimo relativo di una funzione
Teorema fondamentale del massimo/minimo
Ne segue che, per determinare il comportamento dei punti in cui la derivata prima si annulla, dobbiamo studiare il segno della stessa derivata prima a sinistra e a destra di tali punti.
Avremo un "massimo relativo" se la funzione sarà crescente a sinistra e decrescente a destra del punto.
Avremo un "minimo relativo" se la funzione sarà decrescente a sinistra e crescente a destra del punto.
Avremo un "flesso a tangente orizzontale" se la funzione sarà crescente / decrescente sia a sinistra che a destra del punto.
Per ottenere il "massimo / minimo assoluti", una volta determinati gli estremanti relativi, dobbiamo fare due ulteriori passaggi, e cioè verificare il comportamento di f(x) agli estremi dell'intervallo di definizione e determinare il valore che la funzione assume in tutti i punti in cui non è derivabile.
I punti di "massimo / minimo assoluto" saranno dati dal valore più grande / piccolo che la funzione assume tra tutti quelli trovati qui sopra.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Cuspidi, punti angolosi e flessi a tangente verticale
La funzione potrebbe anche non essere derivabile in alcuni punti. Vediamo in quali modi si potrebbe presentare tale funzione.
Data la funzione 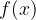 non derivabile in
non derivabile in 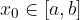 :
:
Quando i limiti destro e sinistro del rapporto incrementale nel punto in cui la funzione non è derivabile esistono entrambi finiti ma assumono valori diversi, abbiamo un punto angoloso.
(un esempio immediato è quello della funzione modulo)
Se i due limiti del rapporto incrementale sinistro e destro sono infiniti di segno opposto, abbiamo un punto di cuspide.
(un esempio immediato è quello della funzione con radice quadrata)
Se infine i due limiti sono infiniti ma dello stesso segno, abbiamo un flesso a tangente verticale.
(un esempio immediato è quello della funzione con radice cubica)
Derivata seconda: concavità, convessità e punti di flesso
Affrontiamo ora l'ultimo passaggio prima di effettuare il disegno definitivo del grafico della funzione da studiare.
Vogliamo individuare la concavita' o la convessita' della funzione ed anche i suoi punti di flesso.
A tale scopo calcoliamo la derivata della derivata prima della funzione y=f(x) ovvero
Ponendo la derivata seconda maggiore di zero e risolvendo la disequazione avremo gli intervalli in cui la funzione rivolge la concavita' verso l'alto, mentre gli intervalli in cui la derivata è negativa, saranno quelli in cui la funzione è convessa.
Teorema per la determinazione della concavità e convessità di una funzione
I punti in cui la derivata seconda si annulla sono quelli in cui la funzione cambia di concavita' (cioe' i punti di flesso).
Il flesso in 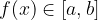 è quel punto nel quale la funzione è attraversata dalla sua tangente, ovvero il punto nel quale avviene il cambio di concavità.
è quel punto nel quale la funzione è attraversata dalla sua tangente, ovvero il punto nel quale avviene il cambio di concavità.
Teorema per la ricerca dei punti di flesso
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Disegno del grafico
Ora, con tutte le informazioni raccolte nei passaggi precedenti, possiamo tracciare il grafico della nostra funzione seguendo, per esempio, i punti sotto elencati.
Disegnamo gli assi cartesiani e, noto il dominio, cancelliamo le zone del piano cartesiano in cui la funzione non è definita.
Disegnamo le intersezioni con gli assi cartesiani e, usando le informazioni ottenute dallo studio del segno, cancelliamo le zone sotto gli intervalli dell'asse delle x in cui la funzione deve essere positiva e le zone sopra gli intervalli dell'asse delle x in cui la funzione deve essere negativa.
Tracciamo gli eventuali asintoti verticali, orizzontali, obliqui e segnamo gli eventuali punti di discontinuità.
Grazie al calcolo delle derivate prima e seconda, segnamo gli eventuali punti di massimo e minimo, punti di flesso, cuspidi, punti angolosi e flessi.
Utilizzando ancora le informazioni dedotte dallo studio del segno di derivata prima e seconda, consideriamo gli intervalli in cui la funzione deve crescere e decrescere e quelli in cui la funzione è concava e convessa e rappresentiamola graficamente.
Il disegno del grafico ci da una sorta di "prova" dell'esattezza del nostro studio di funzione, infatti, se abbiamo sbagliato qualcosa nello studio, troveremo sicuramente un passaggio che entra in contraddizione con l'errore: ad esempio, se per x che tende a infinito otteniamo un asintoto orizzontale y=-5, ma contemporaneamente per x>0 la la funzione deve essere positiva, ci sarà qualcosa che non va.





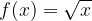 è
è 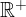 , ma si può scegliere come dominio l'insieme di tutti i reali pari positivi.
, ma si può scegliere come dominio l'insieme di tutti i reali pari positivi.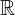 la funzione non è definita, cioè non ha senso calcolarla. In particolare:
la funzione non è definita, cioè non ha senso calcolarla. In particolare: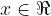 vale l'equazione:
vale l'equazione: 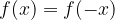
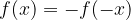
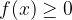
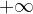 e
e 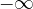 .
.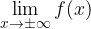
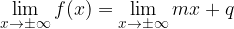
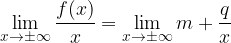
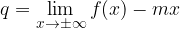
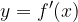
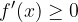
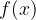 una funzione definita e derivabile in
una funzione definita e derivabile in 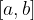 e
e 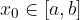 .
.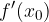 è positiva (negativa) allora la funzione è crescente (decrescente) nel punto, e viceversa.
è positiva (negativa) allora la funzione è crescente (decrescente) nel punto, e viceversa.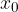 è l'ascissa del punto di massimo (minimo) assoluto se
è l'ascissa del punto di massimo (minimo) assoluto se 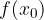 è il valore più grande (piccolo) che la funzione assume nel suo dominio.
è il valore più grande (piccolo) che la funzione assume nel suo dominio.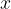 nell'intorno risulti
nell'intorno risulti 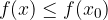 .
.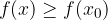 .
.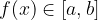 e derivabile, con
e derivabile, con