Il grafico polinomio è una curva continua, che è definita in tutto il campo dei numeri reali. Quando si disegna un grafico del polinomio è necessario conoscere alcune informazioni di base:
valore iniziale, in cui la funzione ha ascissa nulla
comportamento della funzione all'infinito
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Valore iniziale
E' il valore in cui il polinomio interseca l'asse delle ordinate y. E' il termine noto del polinomio:
Il valore iniziale è il punto del polinomio con ascissa nulla (x=0), che corrisponde al termine noto:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Zeri del polinomio
Sono i punti in cui il polinomio interseca l'asse 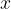 .
.
Gli zeri di un polinomio sono i punti in cui il polinomio vale 0, cioè si annulla:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per la rappresentazione grafica è utile conoscere l'andamento del polinomio negli zeri, cioè se interseca l'asse x o se lo tocca senza attraversarlo.
Comportamento del polinomio nell'intorno degli zeri
Ci interessa ora vedere cosa accade nell'intorno dei singoli zeri. Il grafico del polinomio in un certo punto può comportardi in due modi: o solo toccare l'ascissa oppure attraversare l'asse, cambiando quindi di segno.
Gli zeri individuati possono essere singoli o multipli (ripetuti). Riconosciamo quindi due tipi di zeri:
Il comportamento del grafico nell'intorno degli zeri del polinomio, dipende dal loro grado.
Vicino a zeri di grado dispari, il polinomio cambia di segno e quindi il suo grafico attraversa l'asse x.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nelle vicinanze di zeri di grado pari il polinomio non cambia di segno e quindi tocca solo l'asse delle x.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Comportamento della funzione all'infinito
Per disegnare il grafico del polinomio, studiamone ora il comportamento agli estremi.
Cerchiamo le informazioni necessarie per verificare se agli estremi il nostro grafico è positivo o negativo. Il comportamento del polinomio all'infinito dipende dal termine di grado massimo 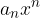 ; saremo quindi in grado di caratterizzare il nostro grafico così:
; saremo quindi in grado di caratterizzare il nostro grafico così:
inizia con valori negativi di y e termina in positivo (crescente)
all'estremo sinistro è positivo e termina con valori negativi di y (decrescente)
inizia e finisce con valori negativi di y (concava)
inizia e finisce con valori positivi di y (convessa)
Vediamo come il termine 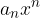 influisce sul grafico. Siamo interessati al segno del grafico, non a valori esatti:
influisce sul grafico. Siamo interessati al segno del grafico, non a valori esatti:
Quando l'argomento di grado massimo è dispari, il segno del grafico agli estremi corrisponderà al segno dell'infinito. Se il coefficiente è positivo, allora il grafico è crescente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quando l'argomento di grado massimo è dispari, il segno del grafico agli estremi corrisponderà al segno dell'infinito. Se il coefficiente è negativo, allora il grafico è decrescente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quando l'argomento di grado massimo è pari, il segno a destra e sinistra è conservato. Se il coefficiente è maggiore di zero, allora il grafico inizia e finisce con valori positivi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quando l'argomento di grado massimo è pari, il segno a destra e sinistra è conservato. Se il coefficiente è minore di zero, allora il grafico inizia e finisce con valori negativi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Estremanti
Per comprendere questo paragrafo è necessario conoscere le derivate.
Gli estremanti sono punti in cui la funzione cambia pendenza. La tangente al grafico nell'estremante è parallela all'asse x.
Un estremante è un punto in cui la derivata si annulla.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





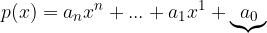
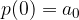
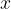 .
.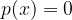
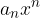 ; saremo quindi in grado di caratterizzare il nostro grafico così:
; saremo quindi in grado di caratterizzare il nostro grafico così: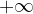 , dobbiamo guardare l'andamento del grafico sul lato destro.
, dobbiamo guardare l'andamento del grafico sul lato destro.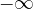 , guarderemo l'andamento del grafico sul lato sinistro.
, guarderemo l'andamento del grafico sul lato sinistro.