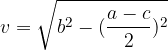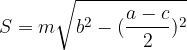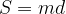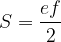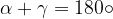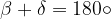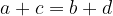Un quadrilatero è un poligono con quattro lati e quattro vertici.
Noi consideriamo soltanto i quadrilateri i cui lati non si intersecano in nessuno dei loro punti interni.
Un quadrilatero con queste caratteristiche si dice semplice.
Un quadrilatero semplice può essere convesso oppure concavo:
Un poligono si dice convesso quando ha le seguenti proprietà:
tutti gli angoli interni sono minori di 180°
qualunque segmento che unisca due vertici è contenuto all'interno della figura o nel suo bordo
Un poligono si dice concavo se ha le seguenti proprietà:
almeno un angolo interno è maggiore di 180° (nel caso del quadrilatero questo può avvenire per uno solo degli angoli interni)
almeno un segmento che unisce due vertici del poligono è totalmente o parzialmente esterno alla figura (nel caso del quadrilatero, questo avviene per una sola coppia di vertici)
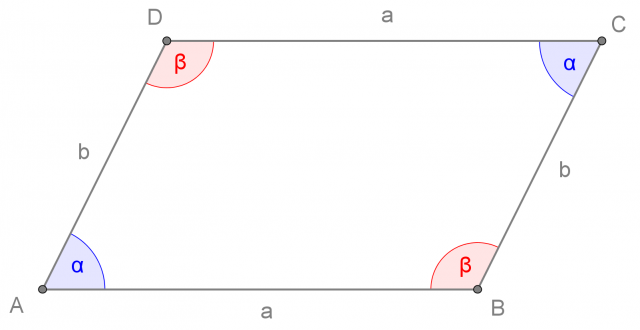
Parallelogramma
Il parallelogramma è un quadrilatero con due coppie di lati paralleli e congruenti, più precisamente le coppie dei lati opposti.
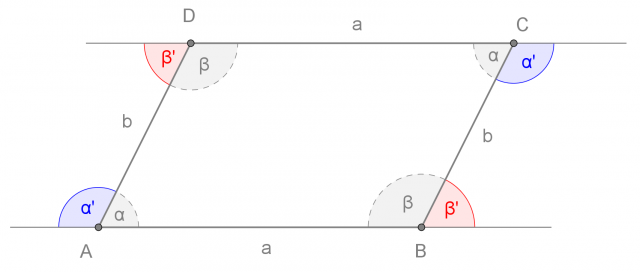
In un parallelogramma, gli angoli interni opposti sono congruenti mentre gli angoli interni adiacenti sono supplementari:
Elementi caratteristici del parallelogramma
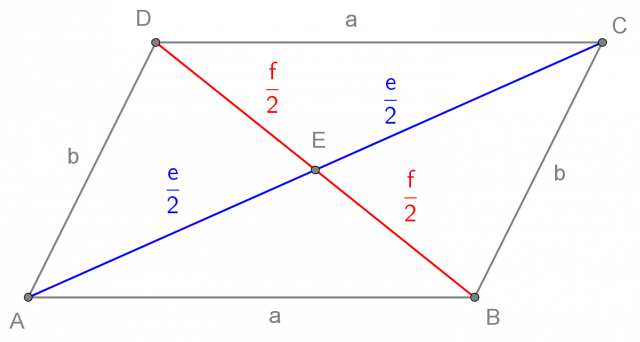
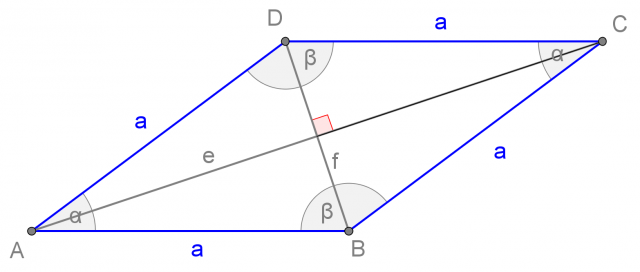
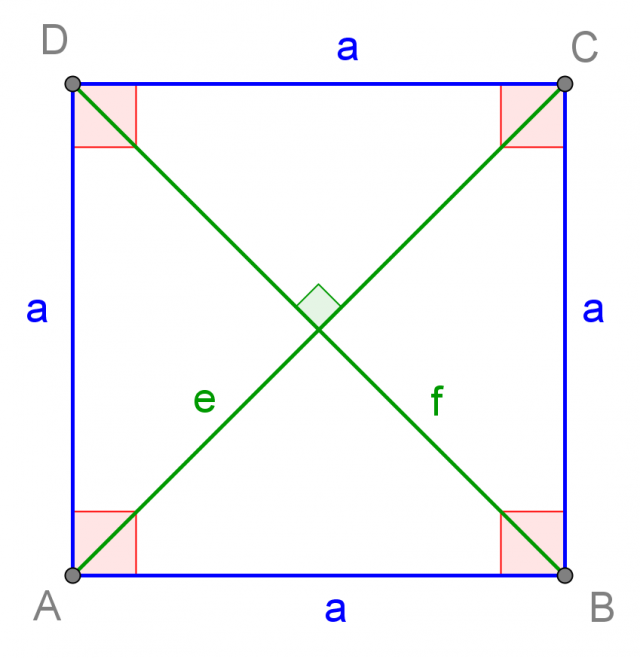
Le diagonali sono i segmenti che uniscono i vertici non adiacenti del parallelogramma.
Un parallelogramma ha due diagonali, che si bisecano, ovvero si incontrano nel loro punto medio.
Nel seguito indichiamo le due diagonali con e in f:
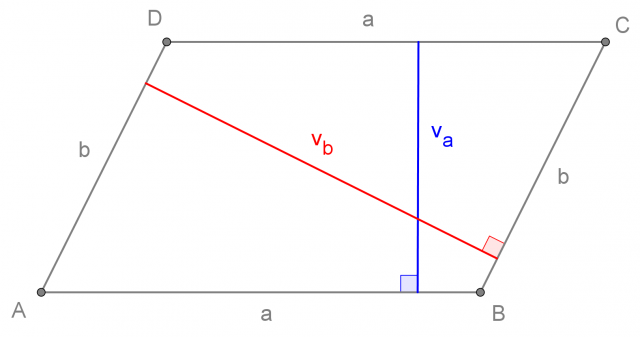
L'altezza del parallelogramma è la distanza tra i lati opposti paralleli.
Un parallelogramma ha due altezze. Le indicheremo con
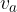 e
e 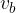 :
:
Gli angoli interni sono gli angoli convessi formati da coppie di lati del parallelogramma che abbiano un vertice in comune,
La somma degli angoli interni di un parallelogramma è di 360° (angolo giro).
La somma degli angoli esterni di un parallelogramma è di 360° (angolo giro).
Parallelogrammi particolari
Rombo
Il rombo è un parallelogramma con i quattro lati congruenti.
Le diagonali del rombo formano tra di loro un angolo retto:
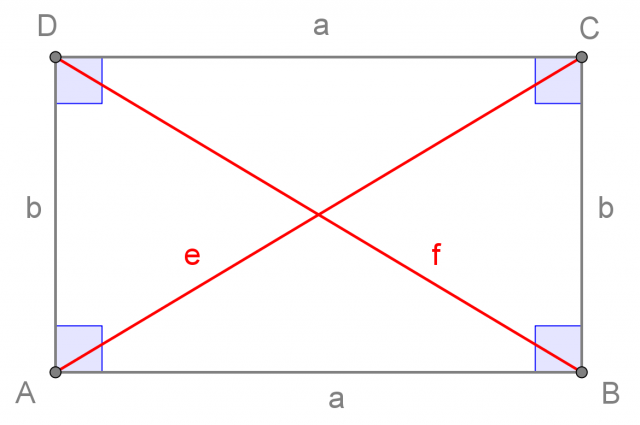
Rettangolo
Il rettangolo è un parallelogramma con i quattro angoli congruenti la cui ampiezza è quindi di 90°. Esso ha anche le diagonali congruenti:
Quadrato
Il quadrato è un parallelogramma che ha contemporaneamente gli angoli e i
lati congruenti. Esso ha quindi anche le diagonali congruenti. Gli angoli interni inoltre sono retti:
Il quadrato è un quadrilatero regolare, poichè ha tutti i lati e tutti gli angoli congruenti.
Perimetro del parallelogramma
Il perimetro di un parallelogramma si calcola come segue:
Formula generale per il perimetro del parallelogramma:
Nei casi particolari, la formula del perimetro è la seguente:
Perimetro del rombo e del quadrato:
Perimetro del rettangolo:
Area del parallelogramma
L'area del parallelogramma si calcola come segue:
Formula generale per l'area del parallelogramma:
Nei casi particolari, la formula dell'area è la seguente:
oppure usando le diagonali:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se scomponiamo un parallelogramma in triangoli rettangoli, possiamo applicare le formule risolutive dei triangoli per calcolarne i diversi elementi (vedi capitolo triangoli).
Trapezio
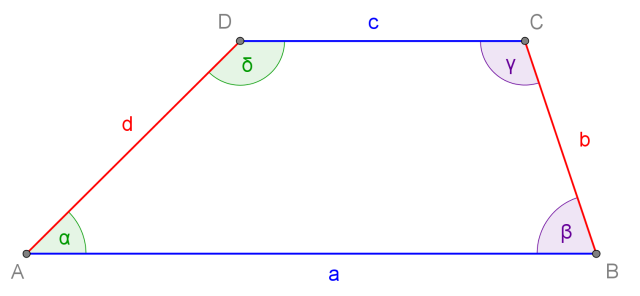
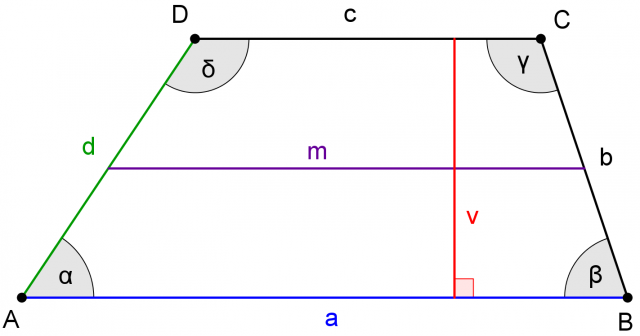
Il trapezio è un quadrilatero con una coppia di lati paralleli opposti tra di loro.
Questi due lati si dicono le basi del trapezio.
Gli altri due lati non paralleli si chiamano lati obliqui.
In ogni trapezio, le coppie di angoli adiacenti a ciascun lato obliquo sono coppie di angoli supplementari.
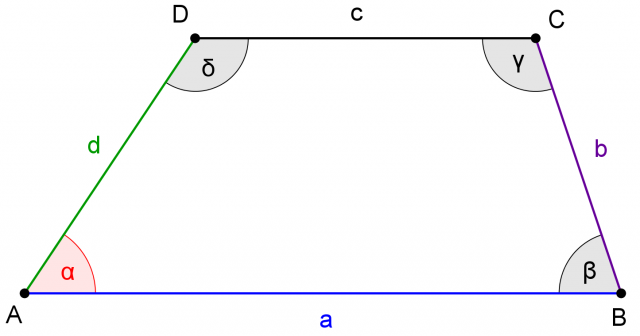
Elementi caratteristici del trapezio
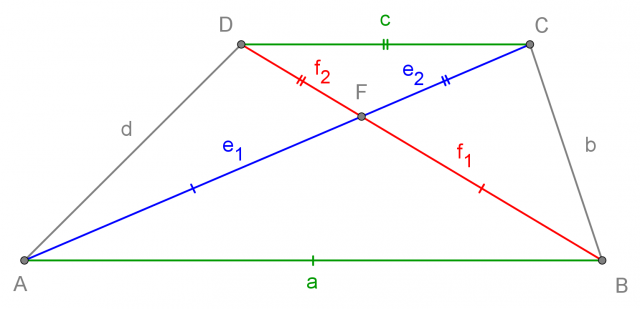
Si chiamano diagonali i segmenti che uniscono coppie di vertici non consecutivi del trapezio.
Il trapezio ha due diagonali:
In ogni trapezio, le diagonali si dividono reciprocamente in segmenti che stanno tra di loro nello stesso rapporto delle due basi:
dove la prima diagonale è
La mediana m è un segmento, parallelo alle due basi a e c, che unisce i punti medi dei lati obliqui b e d del trapezio.
Indicheremo la mediana con la lettera minuscola m.
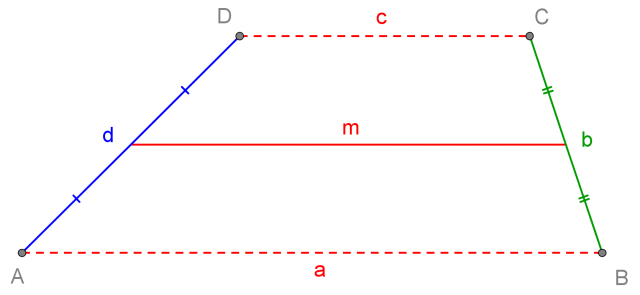
La mediana m è il segmento che unisce i punti medi dei due lati obliqui del trapezio
La lunghezza della mediana è pari alla media aritmetica di a e c:
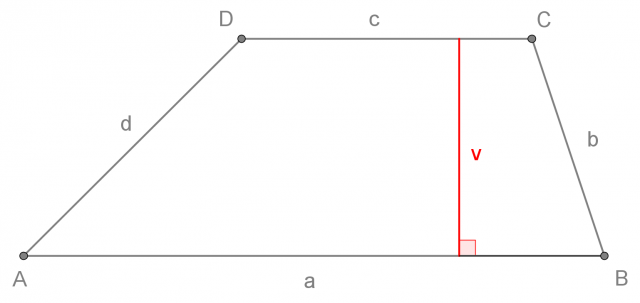
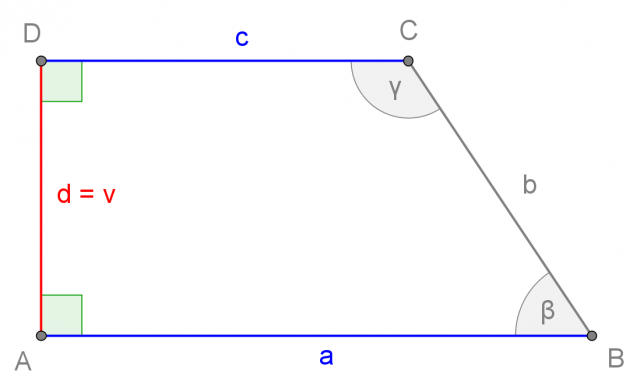
L'altezza del trapezio è la distanza tra le due basi parallele.
Indicheremo l'altezza del trapezio con la lettera v
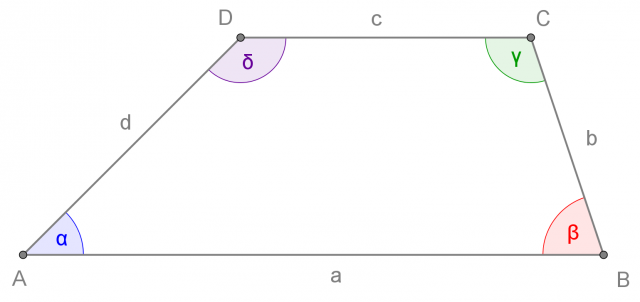
Gli angoli interni del trapezio sono angoli convessi che hanno per vertice i vertici della figura e per lati i lati consecutivi del trapezio.
Di solito indichiamo gli angoli interni con le lettere greche 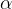 ,
,
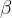 ,
, 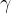 e
e
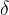 :
:
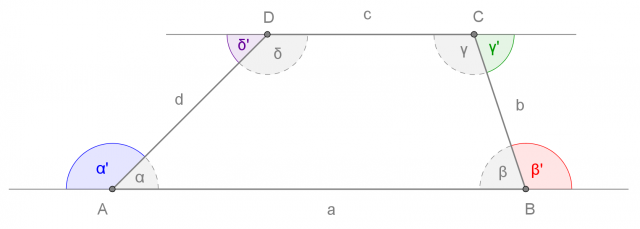
La somma degli angoli interni di un trapezio è di 360° (angolo giro).
La somma degli angoli esterni di un trapezio e' di 360° (angolo giro).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trapezi particolari
Trapezio isoscele
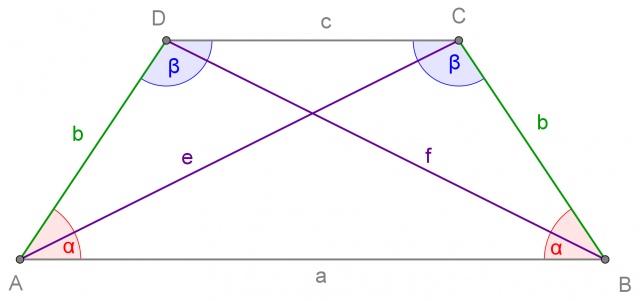
Un trapezio isoscele è un trapezio che ha i due lati obliqui congruenti.
Un trapezio isoscele ha anche gli angoli adiacenti a ciascuna base congruenti, e per simmetria della figura sono congruenti anche le due diagonali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trapezio rettangolo
Un trapezio rettangolo è un trapezio che ha un lato obliquo perpendicolare alle basi. Tale lato obliquo costituisce anche l'altezza del trapezio rettangolo
Perimetro del trapezio
Il perimetro del trapezio si calcola sommando le lunghezze dei quattro lati:
Il perimetro del trapezio è dato dalla seguente formula:
Nei casi particolari il perimetro è dato in questo modo:
Perimetro del trapezio isoscele:
Perimetro del trapezio rettangolo:
Area del trapezio
L'area del trapezio si ricava nel modo seguente:
Formula generale dell'area del trapezio:
ovvero, ricordando l'espressione della mediana m:
Nei trapezi particolari, l'area si può anche esprimere in questo modo:
Area del trapezio isoscele:
Osserviamo che nel trapezio isoscele la proiezione di ciascun lato obliquo sulla base maggiore ha lunghezza 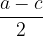 . Applicando il teorema di Pitagora si ha allora:
. Applicando il teorema di Pitagora si ha allora:
L'area del trapezio isoscele si può esprimere quindi con la formula:
Area del trapezio rettangolo:
dove d indica il lato perpendicolare alle basi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Scomponendo il trapezio in triangoli, possiamo applicare a ciascun elemento tutte le proprietà studiate nel capitolo Triangoli.
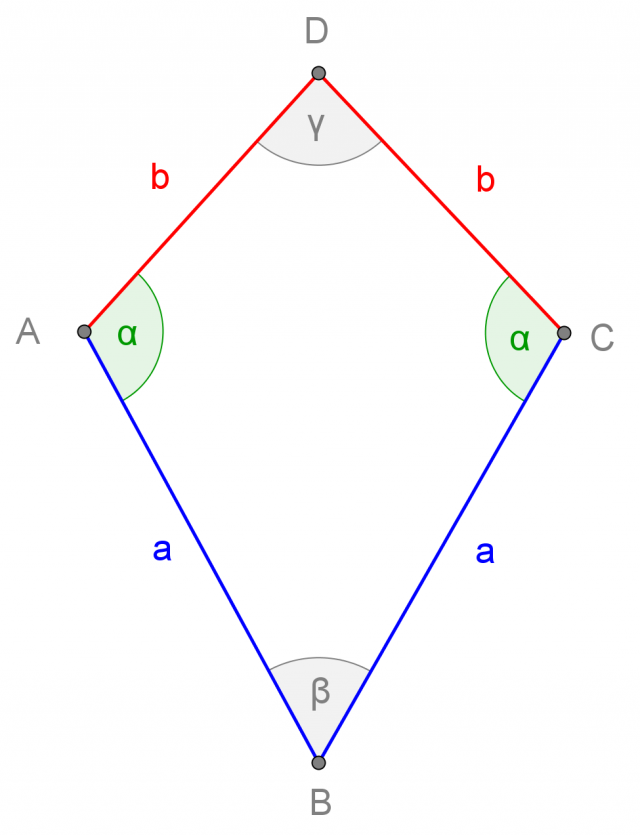
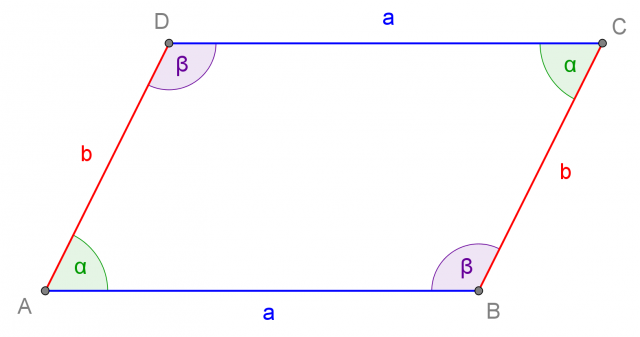
Romboide
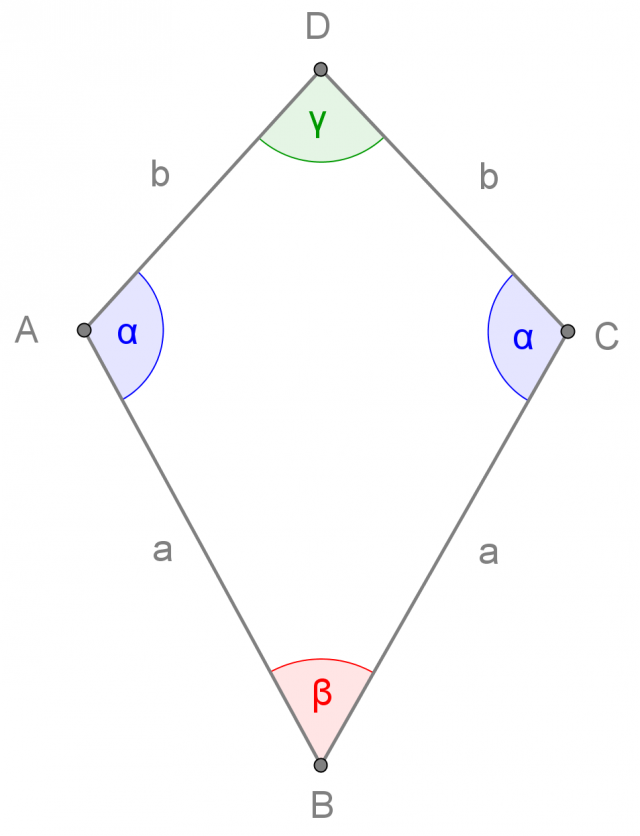
Un romboide è un quadrilatero che ha due coppie di lati consecutivi congruenti tra di loro:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Elementi caratteristici del romboide
Le diagonali sono i segmenti che uniscono vertici non adiacenti del romboide
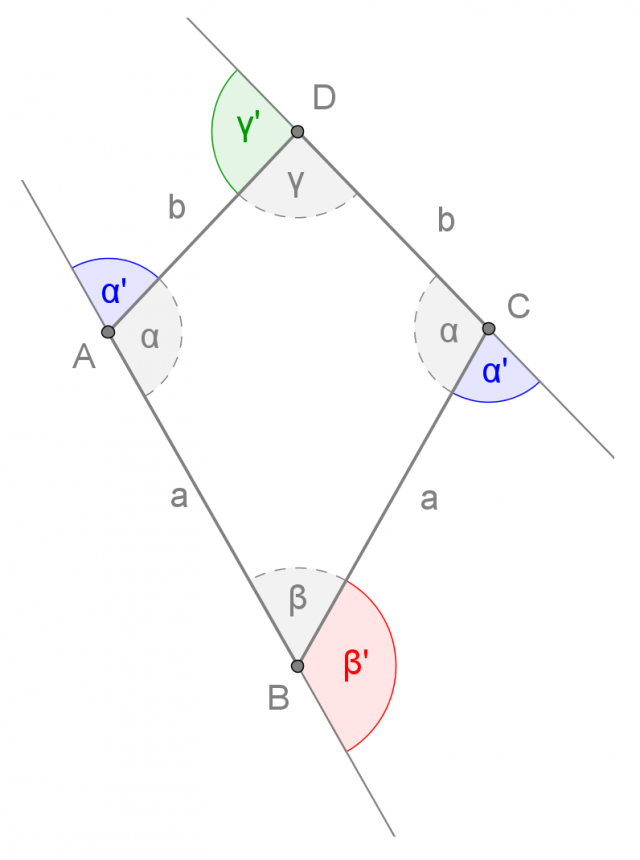
Il romboide ha due diagonali, che formano tra loro un angolo retto. Una delle due diagonali è asse di simmetria della figura e divide la seconda diagonale in due parti uguali:
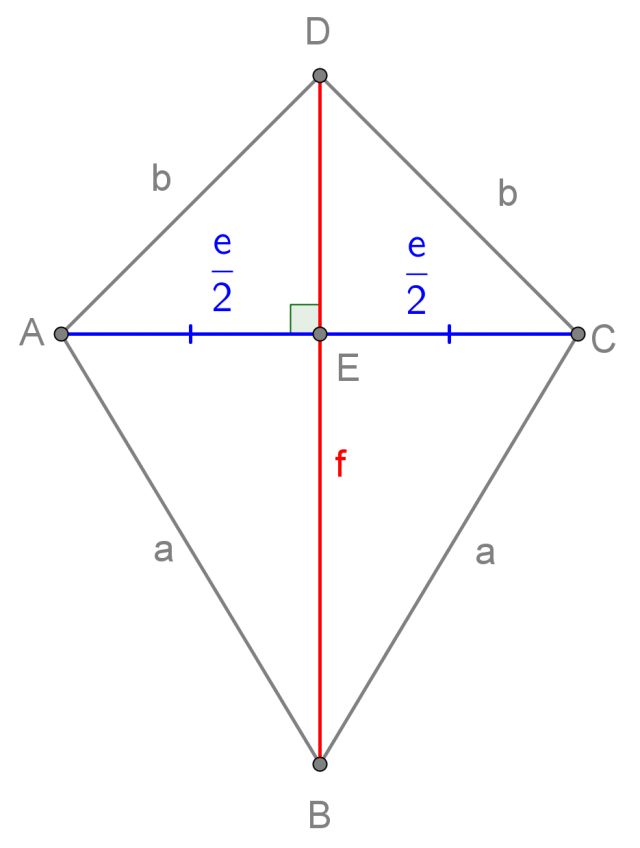
La diagonale f è asse di simmetria della figura ed è perpendicolare alla diagonale e, che divide in due parti uguali
La somma degli angoli interni del romboide è di 360° (angolo giro).
La somma degli angoli esterni del romboide è di 360° (angolo giro).
Perimetro del romboide
Il perimetro del romboide è dato dalla seguente formula:
Area del romboide
L'area del romboide si calcola in questo modo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Scomponendo il romboide in triangoli rettangoli, possiamo calcolarne le diverse parti applicando le proprietà illustrate nel capitolo triangoli.
Altri quadrilateri particolari
Quadrilateri inscrivibili in un cerchio
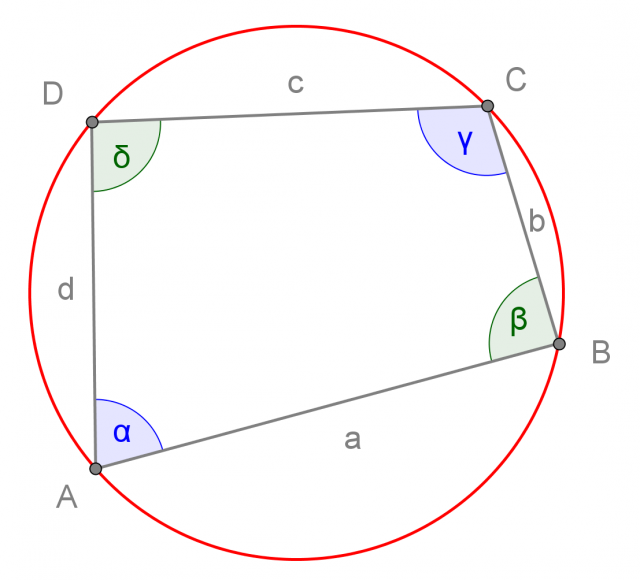
I quadrilateri i cui vertici appartengono tutti ad una stessa circonferenza, sono detti quadrilateri inscrivibili in un cerchio:
Ogni quadrilatero inscrivibile in un cerchio ha gli angoli opposti supplementari:
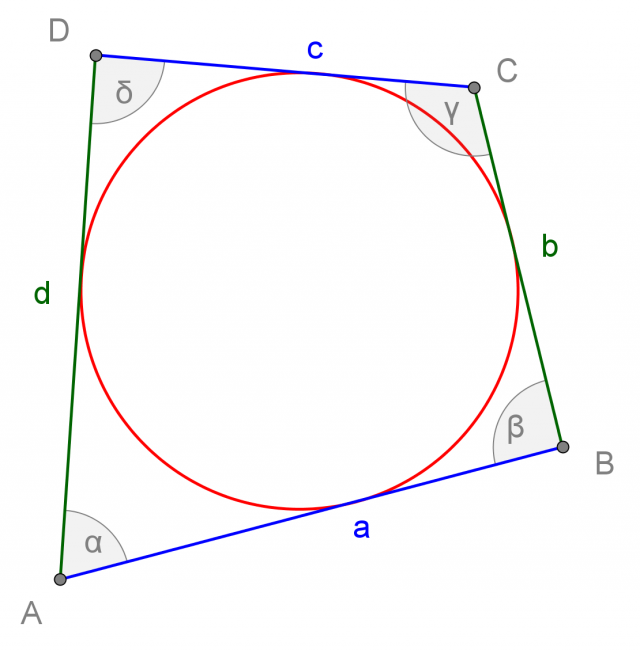
Quadrilateri circoscrivibili ad un cerchio
I quadrilateri i cui quattro lati sono tangenti ad una stessa circonferenza, sono detti quadrilateri circoscrivibili ad un cerchio:
Ogni quadrilatero circoscrivibile ad un cerchio ha le somme dei lati opposti congruenti tra di loro:
Quadrilateri sia inscrivibili sia circoscrivibili
Un quadrilatero che abbia contemporaneamente le seguenti proprietà:
risulta sia inscrivibile sia circoscrivibile ad un cerchio




 e
e  :
:
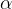 ,
, 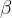 ,
, 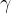 e
e 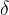 :
:
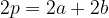
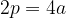
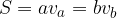
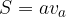
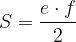
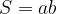
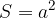
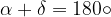
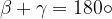
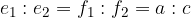
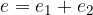
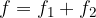

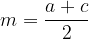
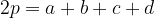
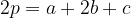
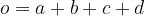
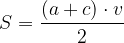
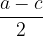 . Applicando il
. Applicando il