In matematica, oltre alla moltiplicazione tra numeri, esiste anche la moltiplicazione tra vettori.
La moltiplicazione tra due vettori è chiamata prodotto scalare.
Tale definizione di moltiplicazione tra vettori è legata con altri concetti di matematica, come ad esempio il teorema di Pitagora, che è il risultato della moltiplicazione di due vettori perpendicolari tra loro.
Definizione di prodotto scalare
Il prodotto scalare di due vettori è uguale al prodotto delle lunghezze (moduli) dei due vettori per il coseno dell'angolo da essi formato:
Il risultato del prodotto scalare tra due vettori è uno scalare.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quando risulta 0 il prodotto scalare di due vettori?
Lunghezza (o modulo) del vettore
Se si effettua il prodotto scalare di un vettore 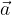 con se stesso, risulta
con se stesso, risulta 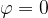 :
:
La lunghezza (o modulo) del vettore 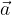 è pari a:
è pari a:
Il calcolo della lunghezza di un vettore conoscendo le sue componenti si effettua allo stesso modo di come studiato nel capitolo su i Vettori in un sistema cartesiano. Qui vediamo un semplice esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proiezione ortogonale
Nel triangolo rettangolo possiamo ricavare la funzione coseno:
Inserendo il risultato ottenuto nella formula del prodotto scalare:
che può essere scritta come:
Il prodotto scalare di due vettori è pari al prodotto della lunghezza del primo vettore per la proiezione del secondo vettore sul primo.
Proprietà del prodotto scalare
Commutativa
Il prodotto scalare gode della proprietà commutativa:
Distributiva
Il prodotto scalare gode della proprietà distributiva:
Omogeneità
Il prodotto scalare è omogeneo:
Il teorema dei coseni
Il teorema dei coseni è spesso usato per risolvere qualsiasi triangolo. Qui analizzeremo la sua applicazione nel caso dei vettori.
E così abbiamo ottenuto il teorema dei coseni che può essere applicato a qualunque lato del triangolo.
Il teorema dei coseni applicato a tutti e tre i lati di un triangolo:
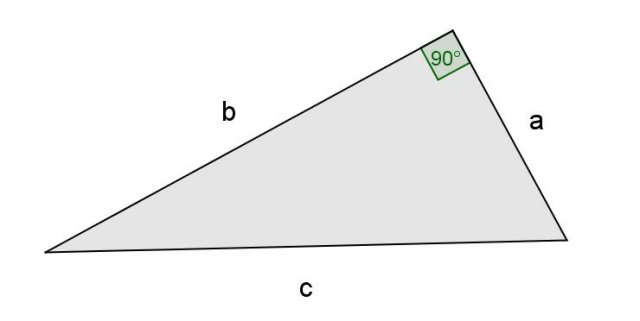
Teorema di Pitagora
Vediamo come il teorema di Pitagora deriva dal teorema dei coseni. Consideriamo un triangolo rettangolo e indichiamo con c l'ipotenusa e con a e b i due cateti:
Applicando il teorema dei coseni:
Il fatto di aver ottenuto il teorema di Pitagora sfruttando il prodotto scalare è una ulteriore prova che la definizione data di prodotto scalare permette di effettuare nella maniera corretta la moltiplicazione tra due vettori.





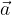 e
e 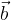 aventi l'origine in comune e formanti un angolo
aventi l'origine in comune e formanti un angolo 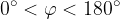 .
.
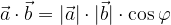
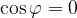 , cioè quando (
, cioè quando (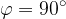 ).
).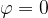 :
: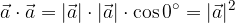
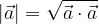
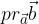 ) si ottiene tracciando una linea retta che parte dal punto finale del vettore
) si ottiene tracciando una linea retta che parte dal punto finale del vettore 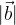 e cateto
e cateto 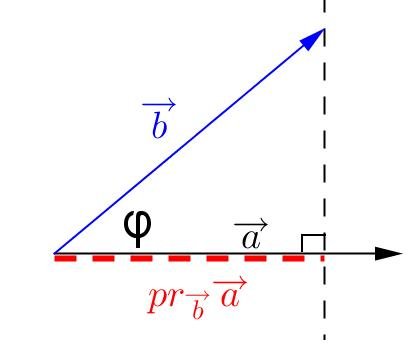
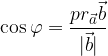
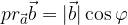
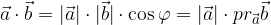
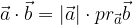
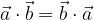
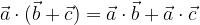
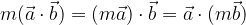
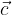 , e l'angolo tra i vettori
, e l'angolo tra i vettori 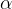 (vedi figura).
(vedi figura).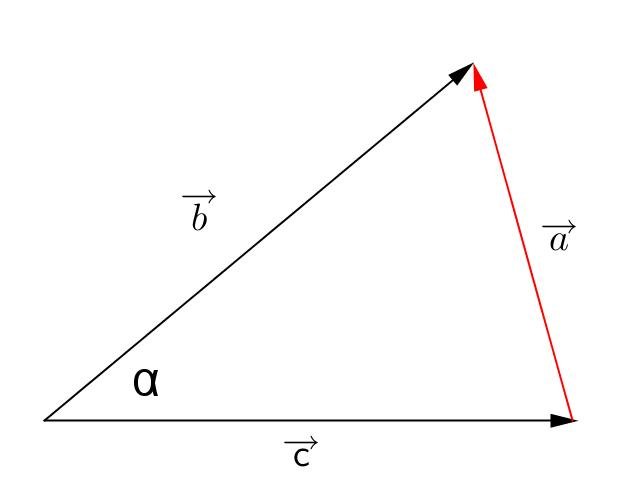
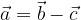
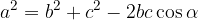
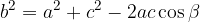
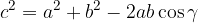
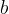 e
e 
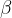 è l'angolo compreso tra i lati
è l'angolo compreso tra i lati 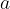 e
e 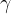 è l'angolo compreso tra i lati
è l'angolo compreso tra i lati