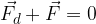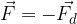Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




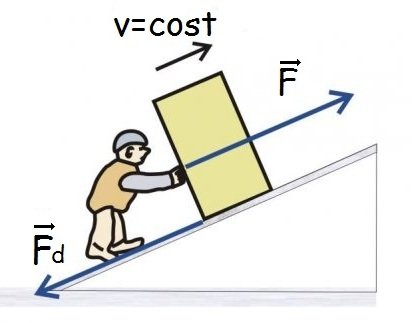
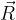 , che è composta da:
, che è composta da: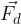 che tende a far scivolare il corpo verso il basso;
che tende a far scivolare il corpo verso il basso;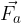 di attrito che si oppone al moto.
di attrito che si oppone al moto.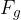 è verticale al terreno e possiamo scomporla in due componenti, perpendicolari tra loro:
è verticale al terreno e possiamo scomporla in due componenti, perpendicolari tra loro: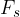 è la componente perpendicolare al pendio;
è la componente perpendicolare al pendio;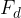 è la componente parallela al piano inclinato.
è la componente parallela al piano inclinato.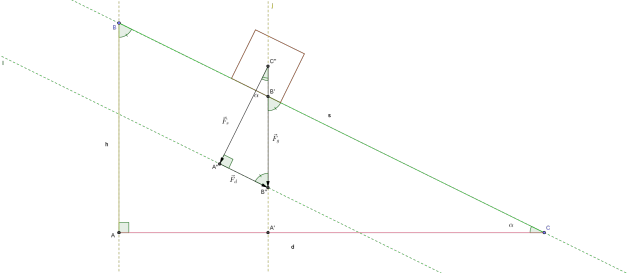
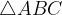 di cateti d e h con ipotenusa s. Dove h è l'altezza del pendio e s la sua lunghezza, con l'angolo
di cateti d e h con ipotenusa s. Dove h è l'altezza del pendio e s la sua lunghezza, con l'angolo 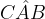 è retto, l'angolo
è retto, l'angolo 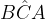 è
è 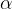 e l'angolo
e l'angolo 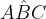 è
è 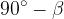 ;
;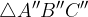 ha ipotenusa
ha ipotenusa 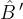 è uguale all'angolo in
è uguale all'angolo in 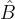 , essendo angoli corrispondenti delle rette parallele passante rispettivamente per AB e A'B' tagliate dalla trasversale passante per BC. Poi vediamo che l'angolo in
, essendo angoli corrispondenti delle rette parallele passante rispettivamente per AB e A'B' tagliate dalla trasversale passante per BC. Poi vediamo che l'angolo in 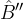 è pari a
è pari a 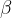 :
: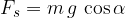
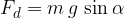
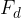 . Possiamo allora rispondere al nostro quesito iniziale, cioè:
. Possiamo allora rispondere al nostro quesito iniziale, cioè: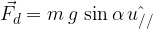
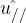 è il versore parallelo al piano. Per mantenere un corpo in equilibrio:
è il versore parallelo al piano. Per mantenere un corpo in equilibrio: