I numeri naturali sono quelli che usiamo per contare, sono fondamentali! Sono numeri natuali:
Anche nella matematica hanno un ruolo fondamentale gli insiemi 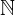 e
e 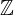 che vanno ad indicare i numeri naturali ed interi. Senza questi numeretti l'intero mondo dei calcoli sfumerebbe in un attimo. Sono loro gli elementi più semplici ma allo stesso tempo più decisivi per far funzionare le cose.
che vanno ad indicare i numeri naturali ed interi. Senza questi numeretti l'intero mondo dei calcoli sfumerebbe in un attimo. Sono loro gli elementi più semplici ma allo stesso tempo più decisivi per far funzionare le cose.
Le operazioni nell'insieme dei numeri naturali
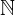 contiene tutti i numeri da 0 ad infinito, ovvero tutti i numeri senza segno davanti. In questo insieme è possibile fare la somma e il prodotto, ma le altre operazioni elementari, quali la sottrazione e la divisione sono un po' limitate.
contiene tutti i numeri da 0 ad infinito, ovvero tutti i numeri senza segno davanti. In questo insieme è possibile fare la somma e il prodotto, ma le altre operazioni elementari, quali la sottrazione e la divisione sono un po' limitate.
Come insieme potro' anche indicarlo come:
che si legge: 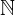 e' l'insieme dei numeri zero, uno, due, tre e avanti così fino ad infinito.
e' l'insieme dei numeri zero, uno, due, tre e avanti così fino ad infinito.

Retta dei numeri naturali
Addizione fra numeri naturali
Possiamo fare tranquillamente qualunque somma all'interno dell'insieme dei numeri naturali
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Arriviamo ad un'importante osservazione.
Il risultato della somma di due numeri naturali è a sua volta un numero naturale, ovvero appartiene all'insieme 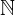
Elemento neutro
Si definisce elemento neutro rispetto alla somma il numero 0: se sommo 0 a qualunque numero, non succede niente. Spiegandoci mediante un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Lo 0 nella somma è neutro, ovvero non sortisce alcun effetto.
Moltiplicazione fra numeri naturali
Anche il prodotto all'interno di due numeri naturali rimane sempre all'interno di 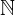 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Elemento neutro
Anche il prodotto possiede un elemento neutro. Tale elemento è il numero 1. Infatti la moltiplicazione tra 1 e un dato numero restituisce quel dato numero. Con un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Elemento nullo
Il prodotto ha una particolarità, moltiplicando un qualsiasi numero per 0 ho come risultato 0. Vediamo un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sottrazione fra numeri naturali
Possiamo sempre eseguire la sottrazione di due numeri naturali. Purtroppo il risultato non sarà sempre nell'insieme dei naturali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il punto di domanda identifica un numero sconosciuto in questo insieme. Più avanti vedremo che questo numeretto è ben definito in un'estensione di 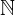 , l'insieme
, l'insieme 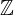 dei numeri interi.
dei numeri interi.
Divisione tra numeri naturali
Possiamo sempre eseguire la divisione di due numeri naturali. Purtroppo il risultato non sarà sempre nell'insieme dei naturali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per risolvere questi problemi dovremo aspettare un'altra estensione di 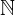 , l'insieme
, l'insieme 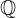 dei numeri razionali.
dei numeri razionali.
Assiomi di Peano
Enunciamo gli Assiomi di Peano, alla base dei Numeri Naturali
Esiste un numero naturale, lo zero.
Ogni numero naturale ha un numero naturale successore.
Numeri diversi hanno successori diversi.
Lo zero non è il successore di alcun numero naturale.
Ogni sottoinsieme di numeri naturali che contenga lo zero e il successore di ogni proprio elemento coincide con l'intero insieme dei numeri naturali (assioma dell'induzione).
Proprietà di N
L'insieme 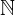 rispetto alla somma e al prodotto gode delle seguenti proprietà, che favoriscono non poco i conti.
rispetto alla somma e al prodotto gode delle seguenti proprietà, che favoriscono non poco i conti.
Proprietà commutativa
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà associativa
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Ordine delle operazioni
Prima di vedere cosa accade se le combiniamo bisogna parlare dell'ordine di operazione.
Prima si eseguono le moltiplicazioni e le divisioni.
Dopo si eseguono addizioni e sottrazioni.
Una precedenza simile avviene tra le parentesi. Detta senza mezzi termini:
Ovvero prima si fanno le operazioni nelle tonde, poi nelle quadre e infine nelle graffe. Gli operatori fuori da tutte le parentesi si considerano per ultimi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà distributiva
Unendo prodotto e somma nelle proprietà si ottiene:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Note su N
Parlando in termini matematici 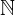 è un insieme chiuso rispetto alla somma e al prodotto e si identifica con la terna
è un insieme chiuso rispetto alla somma e al prodotto e si identifica con la terna 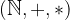 .
.
In questo piccolo ma importante insieme appare un insieme più piccolino che ha delle peculiarità fondamentali per molti teoremi della Matematica.
Numeri Primi
Questo insieme è l'insieme 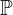 dei numeri primi , ovvero quei numeri che sono divisibili esclusivamente per se stessi e per 1.
dei numeri primi , ovvero quei numeri che sono divisibili esclusivamente per se stessi e per 1.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per completezza inseriamo un tabella dei primi 10 numeri primi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





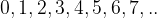
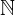 e
e 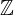 che vanno ad indicare i numeri naturali ed interi. Senza questi numeretti l'intero mondo dei calcoli sfumerebbe in un attimo. Sono loro gli elementi più semplici ma allo stesso tempo più decisivi per far funzionare le cose.
che vanno ad indicare i numeri naturali ed interi. Senza questi numeretti l'intero mondo dei calcoli sfumerebbe in un attimo. Sono loro gli elementi più semplici ma allo stesso tempo più decisivi per far funzionare le cose.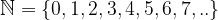

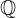 dei
dei 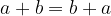
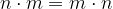
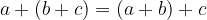
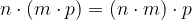


 batte
batte 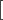 , che a sua volta batte
, che a sua volta batte 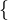
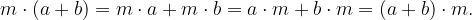
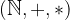
 dei numeri primi , ovvero quei numeri che sono divisibili esclusivamente per se stessi e per 1.
dei numeri primi , ovvero quei numeri che sono divisibili esclusivamente per se stessi e per 1.


