Numeri Interi
I numeri interi (insieme 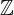 ) sono un'estensione dei numeri naturali (insieme
) sono un'estensione dei numeri naturali (insieme 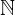 ). Comprendono questi ultimi più tutti i numeri naturali col segno meno davanti, ossia i numeri negativi.
). Comprendono questi ultimi più tutti i numeri naturali col segno meno davanti, ossia i numeri negativi.
Vengono introdotti perché i naturali non sono chiusi rispetto alla sottrazione: se facciamo alcune sottrazioni, potrebbe capitarci di uscire dall'insieme dei numeri naturali per poter calcolare il risultato. Vediamo con un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un insieme di numeri si dice chiuso rispetto ad un'operazione se il risultato di quell'operazione è un numero che appartiene ancora allo stesso insieme;
Un insieme di numeri si dice aperto rispetto ad un'operazione se il risultato di quell'operazione non appartiene sempre all'insieme dei numeri di partenza;
L’insieme 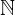 dei numeri naturali è contenuto nell'insieme
dei numeri naturali è contenuto nell'insieme 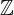 degli interi:
degli interi:
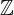 contiene tutti i numeri da meno infinito ad infinito.
contiene tutti i numeri da meno infinito ad infinito.
per un numero intero negativo il segno – (meno) è caratteristica indispensabile per la sua individuazione, dobbiamo indicarlo;
per un numero intero positivo il segno + (più) è facoltativo. Nell'accezione comune, un numero senza segno davanti è positivo.
L’insieme può essere rappresentato come:
oppure con una retta dei numeri interi:
Si può pensare che il numero 0 faccia da specchio: a parte il segno i numeri sono gli stessi a sinistra e a destra dello 0 ed alla stessa distanza. Lo 0 fa da origine: a destra dell’origine abbiamo i numeri positivi, a sinistra i negativi.
I numeri interi sono composti da:
un segno (positivo + oppure negativo -)
un valore assoluto (o modulo), ossia la parte numerica senza segno.
L’unica eccezione è quella dello zero 0, che non ha segno.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il passaggio da numeri naturali 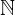 a numeri interi relativi
a numeri interi relativi 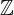 comporta il passaggio dal calcolo aritmetico a quello algebrico.
comporta il passaggio dal calcolo aritmetico a quello algebrico.
Le operazioni nell'insieme dei numeri interi
In questo insieme è possibile fare le operazioni elementari: addizione, sottrazione e moltiplicazione, nel senso che rispetto a queste tre operazioni l'insieme 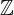 è chiuso. La divisione non è sempre possibile, ossia
è chiuso. La divisione non è sempre possibile, ossia
non è soddisfatta per qualsiasi numero m, n e q appartenente a 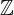 .
.
Addizione e sottrazione fra numeri interi
L’insieme dei numeri interi è chiuso rispetto ad addizione e sottrazione: i risultati di queste operazioni sono ancora numeri interi.
La presenza del segno nei numeri interi rende le operazioni, in prima battuta, meno intuitive. Consideriamo allora il seguente segmento dei numeri interi compreso tra -10 e +10, estratto dalla retta degli interi intorno allo 0, con una quantità di numeri pari a 21 (dieci tra -10 e -1, più dieci tra +1 e +10, più lo 0).
Inoltre, prima di partire con gli esempi, è utile menzionare le quattro regolette di semplificazione delle parentesi che useremo davanti ai numeri.
Per eliminare le parentesi devo ricordare che:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Numeri concordi e discordi per la somma
E’ possibile generalizzare le operazioni di somma introducendo il concetto di numeri relativi concordi e discordi.
Per concordi si intendono due numeri con lo stesso segno, per discordi due numeri con segno opposto. Pertanto si può affermare:
la somma di due numeri relativi concordi è un numero relativo concorde con gli addendi, il cui valore assoluto è la somma dei due valori assoluti
la somma di due numeri relativi discordi è un numero relativo con segno uguale a quello del numero di modulo maggiore e valore assoluto uguale alla differenza tra i due valori assoluti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La differenza
Chiarito il meccanismo della somma con i numeri concordi, soffermiamoci sulla differenza. Abbiamo già visto in alcuni esempi come il segno meno della sottrazione davanti ad un numero di un segno qualsiasi fa cambiare il segno di quel numero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In altre parole, in algebra sottrarre un numero equivale ad addizionare il suo opposto. Quindi possiamo dire che ogni sottrazione può essere trasformata in addizione, cambiando il segno al numero preceduto dal segno meno di sottrazione.
L’addizione algebrica
Come detto all’inizio, i numeri interi relativi appartengono al mondo dell’algebra, quindi le operazioni con questi numeri si chiamano algebriche. Si parla infatti di addizione algebrica per indicare un’operazione tra somma, differenza o mista, contenente numeri di entrambi i segni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Elemento neutro della somma algebrica
Per le operazioni di addizione algebrica l’elemento neutro dell’insieme 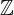 è lo stesso dell’insieme
è lo stesso dell’insieme 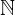 , ossia lo 0. Sommando o sottraendo 0 a qualsiasi numero intero quel numero rimane invariato.
, ossia lo 0. Sommando o sottraendo 0 a qualsiasi numero intero quel numero rimane invariato.
Lo zero 0 è anche il risultato della somma di due numeri opposti, aventi cioè stesso valore assoluto ma segno contrario, ad esempio
Moltiplicazione fra numeri interi
Come anticipato, anche per la moltiplicazione l’insieme 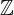 dei numeri interi è chiuso, ossia ogni risultato di un prodotto appartiene ancora a
dei numeri interi è chiuso, ossia ogni risultato di un prodotto appartiene ancora a 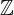 . Però rispetto ai naturali per la presenza del segno occorre fare considerazioni aggiuntive. Il prodotto tra due numeri interi è anch'esso un intero con segno. Ecco allora la tabellina utile a trovare il segno del risultato:
. Però rispetto ai naturali per la presenza del segno occorre fare considerazioni aggiuntive. Il prodotto tra due numeri interi è anch'esso un intero con segno. Ecco allora la tabellina utile a trovare il segno del risultato:
Segno nelle moltiplicazioni
due numeri interi concordi moltiplicati tra loro daranno sempre un numero positivo, con il valore assoluto uguale al prodotto dei due valori assoluti
due numeri interi discordi daranno sempre un numero intero negativo, sempre con il valore assoluto uguale al prodotto dei due valori assoluti.
Il simbolo per, generalmente indicato con 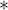 si può indicare anche con un puntino:
si può indicare anche con un puntino:  .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In generale vale la considerazione che è il segno meno – a far cambiare il segno del risultato finale rispetto ai numeri da moltiplicare; in altre parole la presenza del solo segno più + non inverte il segno del risultato.
Se estendiamo questo concetto alla moltiplicazione tra più di due numeri interi si avrà che:
per una quantità pari di numeri negativi il risultato finale ha segno positivo;
per una quantità dispari di numeri negativi il risultato finale ha segno negativo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Elemento neutro della moltiplicazione
Per le operazioni di moltiplicazione l’elemento neutro dell’insieme 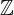 è il numero +1. Facendo il prodotto tra un numero qualsiasi di
è il numero +1. Facendo il prodotto tra un numero qualsiasi di 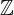 e +1 si otterrà lo stesso numero di partenza. Chiaramente qui il segno positivo del +1 è fondamentale.
e +1 si otterrà lo stesso numero di partenza. Chiaramente qui il segno positivo del +1 è fondamentale.
Non è possibile usare come elemento neutro il numero -1, perchè lascerebbe invariato solo il valore assoluto del numero originario ma ne cambierebbe il segno.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione tra numeri interi
Per la divisione bisogna usare la stessa tabellina dei segni vista per la moltiplicazione. Perciò
la divisione tra due numeri concordi dà un numero positivo, la divisione tra due numeri discordi ne dà uno negativo; in entrambi i casi il valore assoluto si ottiene come divisione tra i due valori assoluti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà di 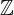
L'insieme 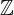 rispetto alla somma algebrica e al prodotto gode delle stesse proprietà dell’insieme dei naturali
rispetto alla somma algebrica e al prodotto gode delle stesse proprietà dell’insieme dei naturali 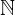 , ossia:
, ossia:
per qualsiasi numero a, b, c, m, n, p intero relativo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Queste proprietà sono ovviamente estendibili ad operazioni con più di tre numeri.
Ordine delle operazioni
Nelle operazioni miste, contenenti più tipi di operazioni elementari tra numeri interi relativi, è necessario applicare un ordine ben preciso. In particolare:
1. moltiplicazione e divisione (segni  e
e  ) sono da fare per prime
) sono da fare per prime
Devo ricordare la regola generale secondo cui:
le operazioni vanno svolte a partire dai numeri contenuti nelle tonde, per poi passare alle quadre, finendo con quelle contenute nelle graffe.
Quando non ci sono più parentesi l’operazione si sarà ridotta in modo elementare, ossia con soli due numeri.
Le regole di priorità nelle operazioni vanno eseguite allo stesso livello di parentesi, ossia posso fare prima un’addizione fuori dalle parentesi anche se dentro non ho ancora calcolato un prodotto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





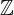 ) sono un'estensione dei
) sono un'estensione dei 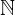 ). Comprendono questi ultimi più tutti i numeri naturali col segno meno davanti, ossia i numeri negativi.
). Comprendono questi ultimi più tutti i numeri naturali col segno meno davanti, ossia i numeri negativi.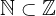
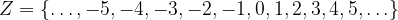

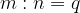
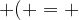
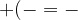
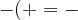
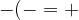
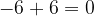

 si può indicare anche con un puntino:
si può indicare anche con un puntino:  .
.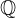 .
.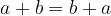

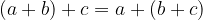
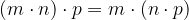
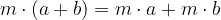
 ) sono da fare per prime
) sono da fare per prime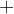 e
e  ), da fare quando si sono esauriti i segni
), da fare quando si sono esauriti i segni 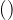 e le quadre
e le quadre  , le successive sono le graffe
, le successive sono le graffe 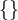 .
.


